Initialy spring in its natural length now a block at mass 0.25 kg is released then find out maximum force by system on floor ?
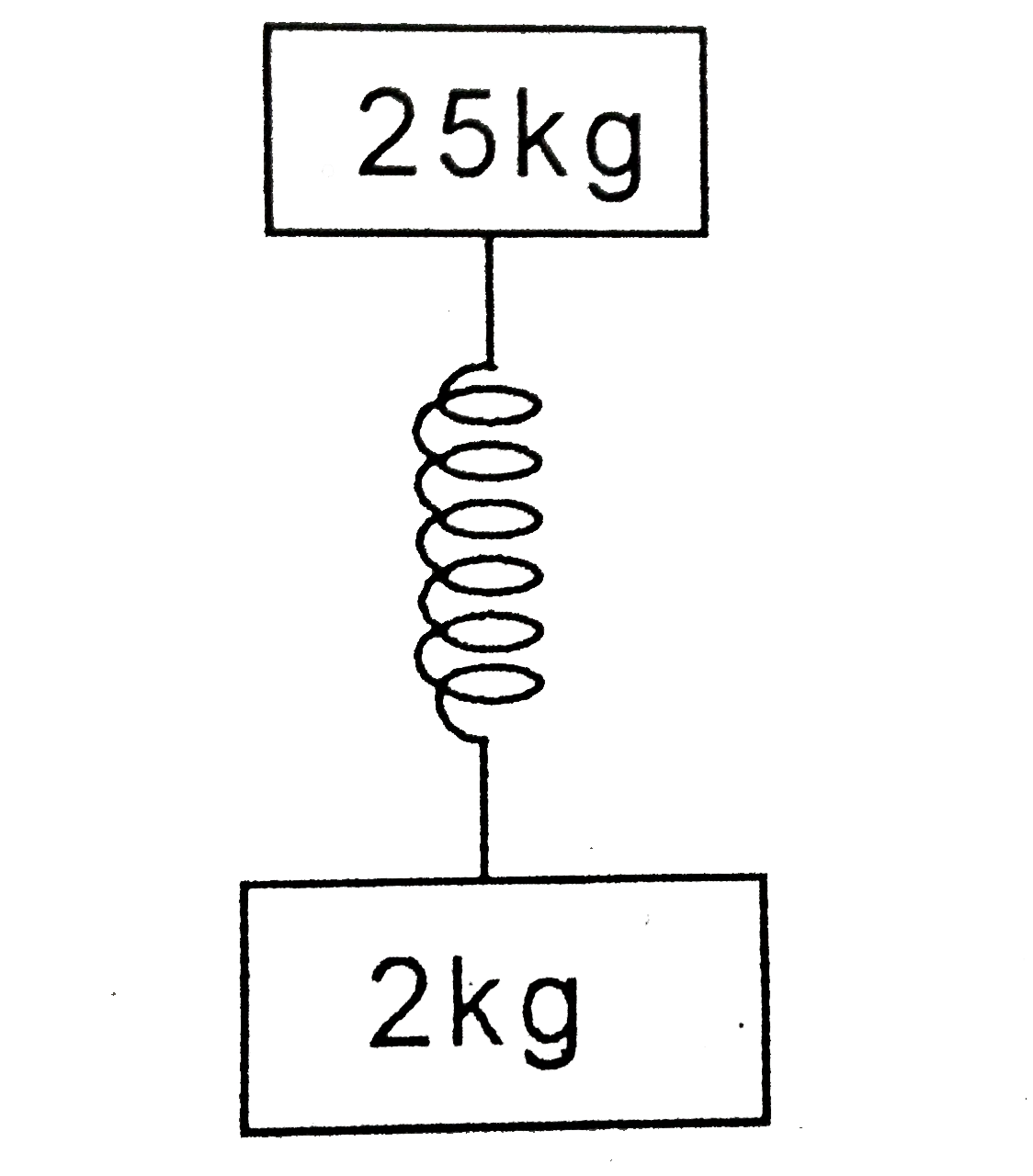
15 N
20 N
25 N
30 N
The correct Answer is:C
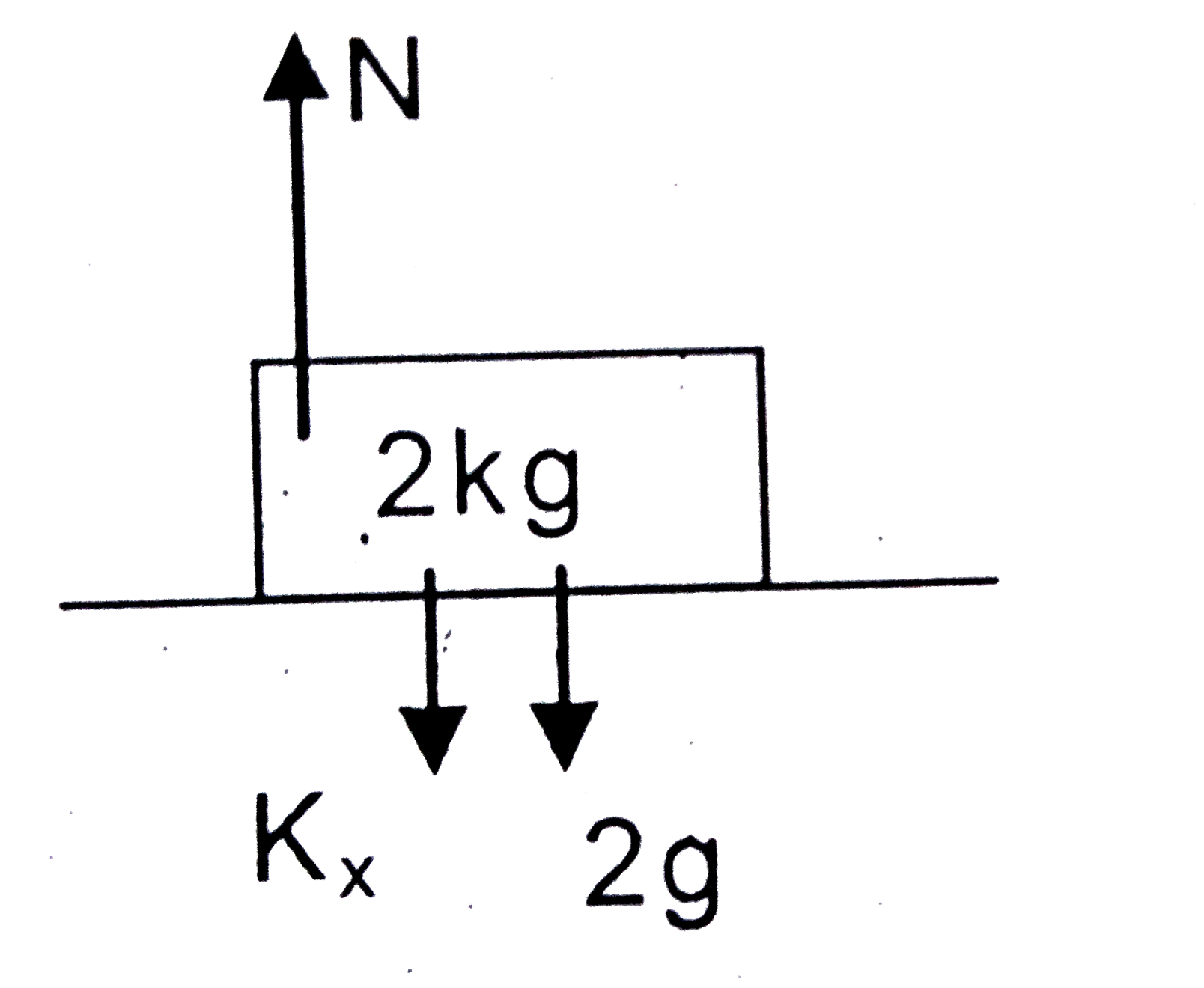
Work - energy theory on (25) kg
12Kx2=mgx
Kx=2mg
Kx=2×.25×10
=5N
= 25 N
N=kx+2g
=5+20=25N
Topper's Solved these Questions
Similar Questions
Initially spring is in natural length and block of mass m is released from rest what should be the minimum value of M (in kg) to just move the 2kg block. If this minimum value is x8kg. Find x

View SolutionInitialy spring is in the natural length and blocks A&B are at rest. Find maximum value of constant force F that can be applied on B such that block A remains at rest. (g=10m/s2) (given answer in Newton)
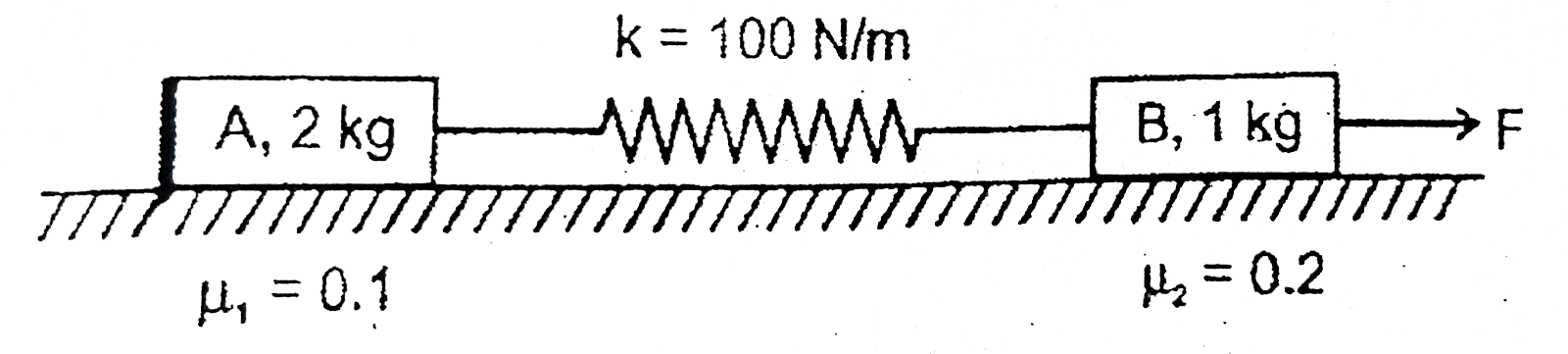
View Solution
Knowledge Check
A block of mass m is attached to a spring of force constant k whose other end is fixed to a horizontal surface. Initially the spring is in its natural length and the block is released from rest. The average force acting on the surface by the spring till the instant when the block has zero acceleration for the first time is
 AmgπB2mgπC3mgπD4mgπ
AmgπB2mgπC3mgπD4mgπBlock A of mass m is placed on a plank B . A light support S is fixed on plank B and is attached with the block A with a spring of spring constant K. Consider that initialy spring is in the natural length, and the system is at rest. Find the maximum compression in the spring, if the plank B is moved with a constant acceleration 'a' . (All the surface are smooth) :
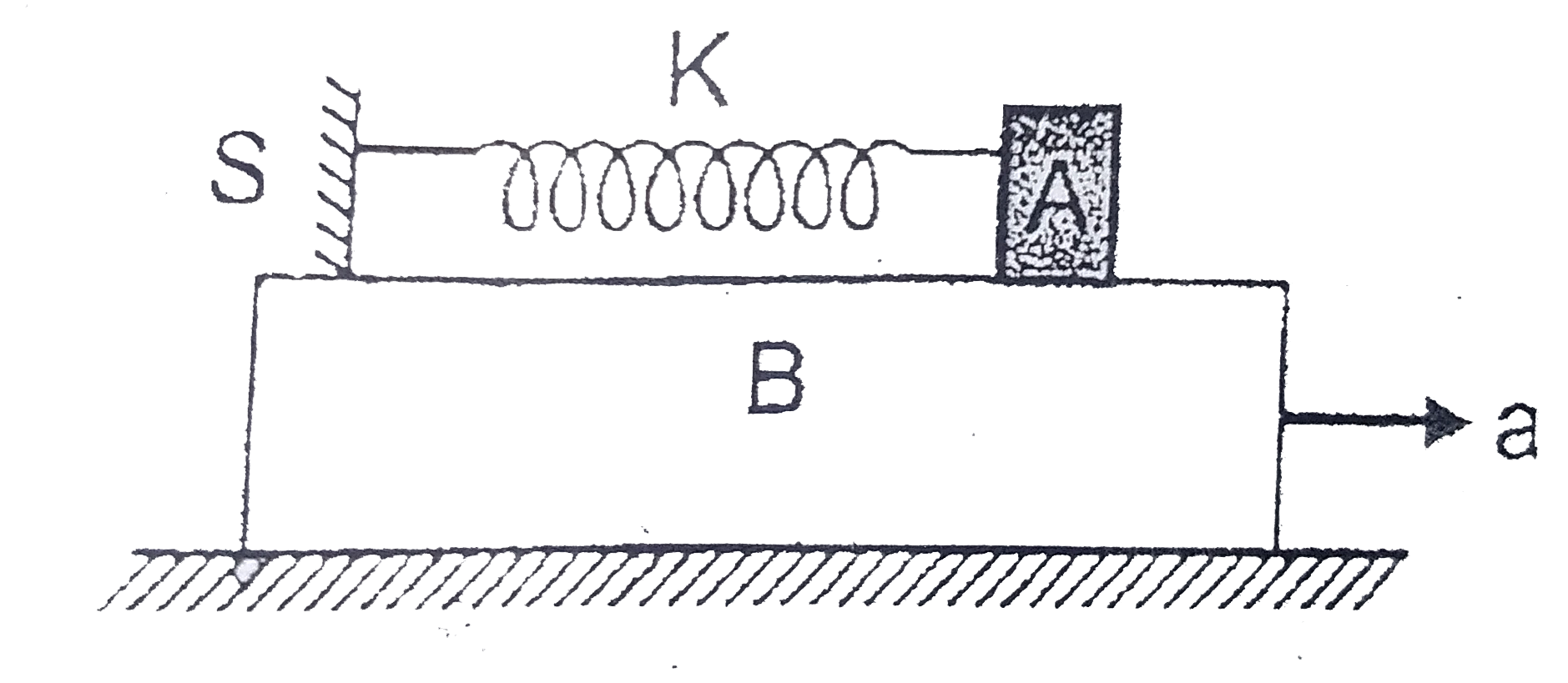 Ama2KB2maKCmaKD2maK
Ama2KB2maKCmaKD2maKInitially spring is in its natural length . The block of mass 3kg in contact with rigid wall . The block of mass 1kg is pushed through a distance 4cm towards the wall and then released. The velocity of the center of mass when the block of mass 3kg breaks off the wall is (k=100N/m)
 A0.1m/sB0.2m/sC0.3m/sD0.4m/s
A0.1m/sB0.2m/sC0.3m/sD0.4m/s
A block of mass m is connected to a spring (spring constant k). Initially the block is at rest and the spring is in its natural length. Now the system is released in gravitational field and a variable force F is applied on the upper end of the spring such that the downward acceleration of the block is given as a=g−αt, where t is time elapses and α=1m/s2, the velocity of the point of application of the force is:
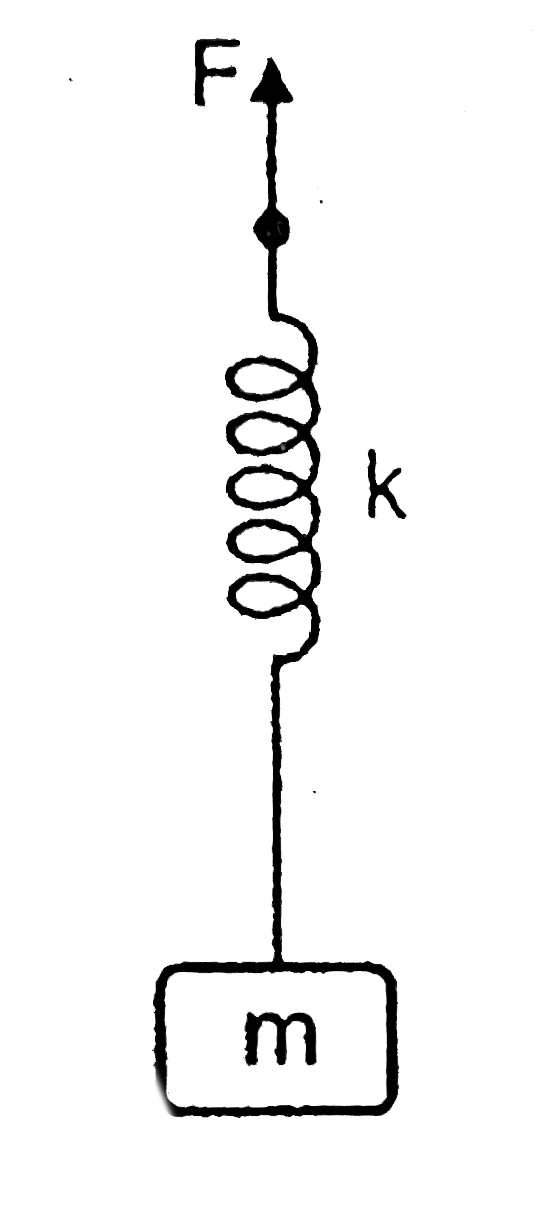
View SolutionA block of mass m attached with a spring and held by a person such that the spring is in natural length l0. Now the man releases the block, the ratio of maximum compression in the spring in the given situation , to that of the compression at equilibrium position.

View SolutionA block of mass M is kept on a smooth surface and touches the two springs as shown in the figure but not attached to the springs. Initially springs are in their natural length. Now, the block is shifted (l0/2) from the given position in such a way that it compresses a spring and released. The time - period of oscillation of mass will be

View SolutionFind the maximum tension in the spring if initially spring at its natural length when block is released from rest.

View SolutionA spring of natural length l is compressed vertically downward against the floor so that its compressed lengtg becomes 12. On releasing, the spring attins its natural length. If k is the siffness constant of spring, then the work done by the spring on the floor is
View Solution
