using the illustration when both surfaces 1 and 2 are exposed to the atmoshere, P1 and P2 are gauge pressure , and h1 and h2 are heights .

The Bernoulli equation for this situation is h1+P1W+V212a=h2+P2W+V222a
If an Identical outlet were placed at exactly the same point on the left side of the container, the velocity would be
zero
computable
2V2
none of the above
The correct Answer is:B
The question is self - explanatory
Topper's Solved these Questions
Similar Questions
H.W - 1 & 2
View SolutionTwo thermally insulated vessels 1 and 2 are filled with air and connected by a short tube equipped with a valve. The volumes of the vessels, the pressures and temperature of air in them are know (V1,p1,T1 and V2,p2,T2). Find the air temperature and pressure established after the opening of the valve.
View Solution
Knowledge Check
using the illustration when both surfaces 1 and 2 are exposed to the atmoshere, P1 and P2 are gauge pressure , and h1 and h2 are heights .

The Bernoulli equation for this situation is h1+P1W+V212a=h2+P2W+V222a
The value of P1 and P2 are such thatAP1=P2=0BP2 lt P1CP1>P2DP1/P2=0using the illustration when both surfaces 1 and 2 are exposed to the atmoshere, P1 and P2 are gauge pressure , and h1 and h2 are heights .
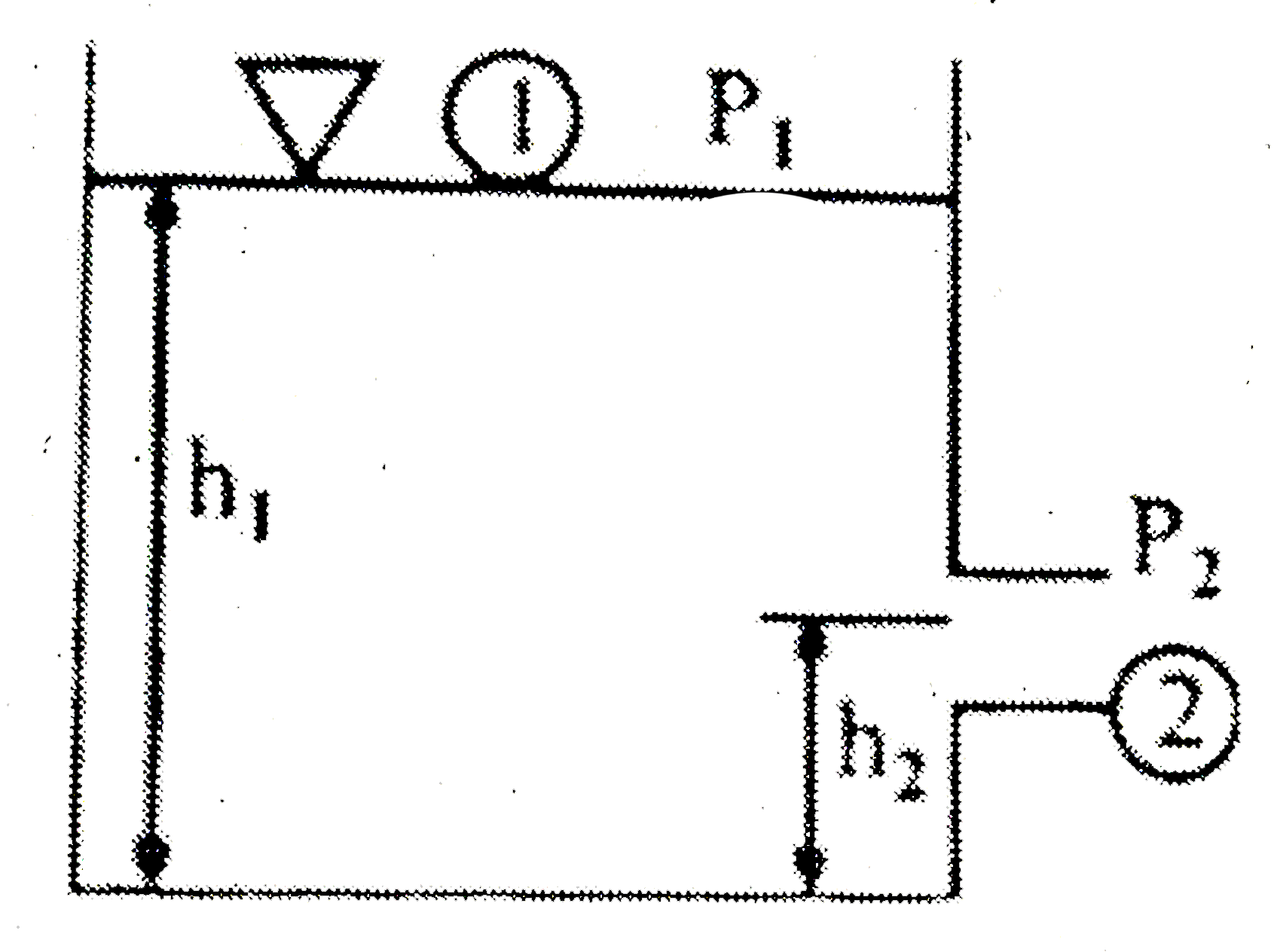
The Bernoulli equation for this situation is h1+P1W+V212a=h2+P2W+V222a
The velocity of the fluid leavening point (2) is constant and can be expressed asAV2=(P1/P2)V1BV2=(P1/P2)ahCV2=[(h1−h2)(2a)]1/2Dnone of the aboveIf r1,r2,r3 are in H.P. then the sides are in
AG.P.BH.PCA.P.Dnone
The top surface of an incompressible liquid is open to the atmosphere. The pressure at a depth h1 below the surface is p1 . What is the pressure p2 at depth h2=2h1 compare with p1 ?
View SolutionIf r1,r2,r3 in a triangle be in H.P. then the sides are
View SolutionA horizontal tube has different cross sections at points A and B. The areas of cross section are a1 and a2 respectively, and pressures at these points are p1=ρgh1 and p2=ρgh2 where ρ is the density of liquid flowing in the tube and h1 and h2 are heights of liquid columns in vertical tubes connected at A and B. If h1−h2=h, then the flow rate of the liquid in the horizontal tube is
View SolutionAt two points on a horizontal tube of varying cross-section, the radii are 1 cm and 0.4 cm, velocities of the fluid are v1 and v2 and the pressure difference (P1−P2) between these point is 4.9 cm of water Then the value of √v22−v21 is
View SolutionThe cell reaction for the given cell is spontaneous if:
Pt,H2(P1atm)∣∣H+(1M)∣∣H2(P2atm),Pt
View Solution
