Two thermally insulated vessels 1 and 2 are filled with air and connected by a short tube equipped with a valve. The volumes of the vessels, the pressures and temperature of air in them are know $(V_{1}, p_{1}, T_{1}$ and $V_{2}, p_{2}, T_{2}$ ). Find the air temperature and pressure established after the opening of the valve.

Video Solution

Text Solution

Verified by Experts

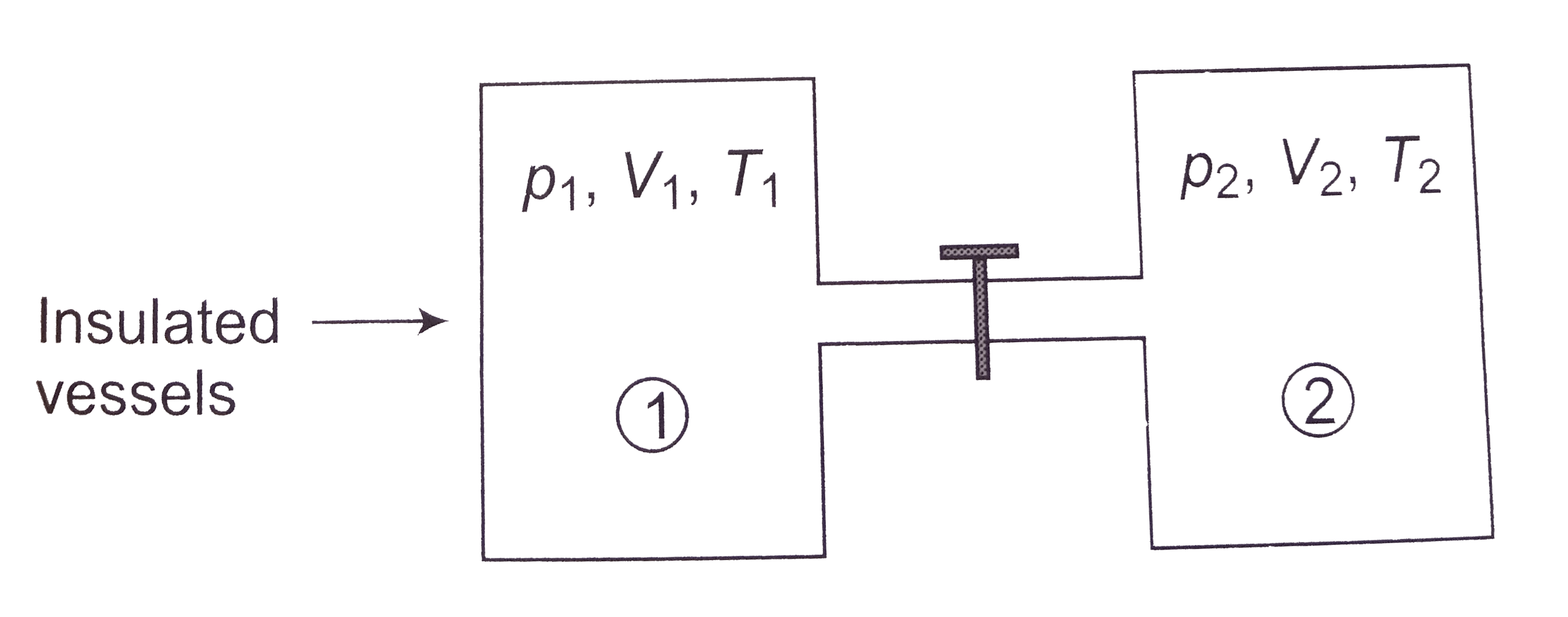
After opening of valve, the pressure and temperature in two chambers becomes same (after long time).

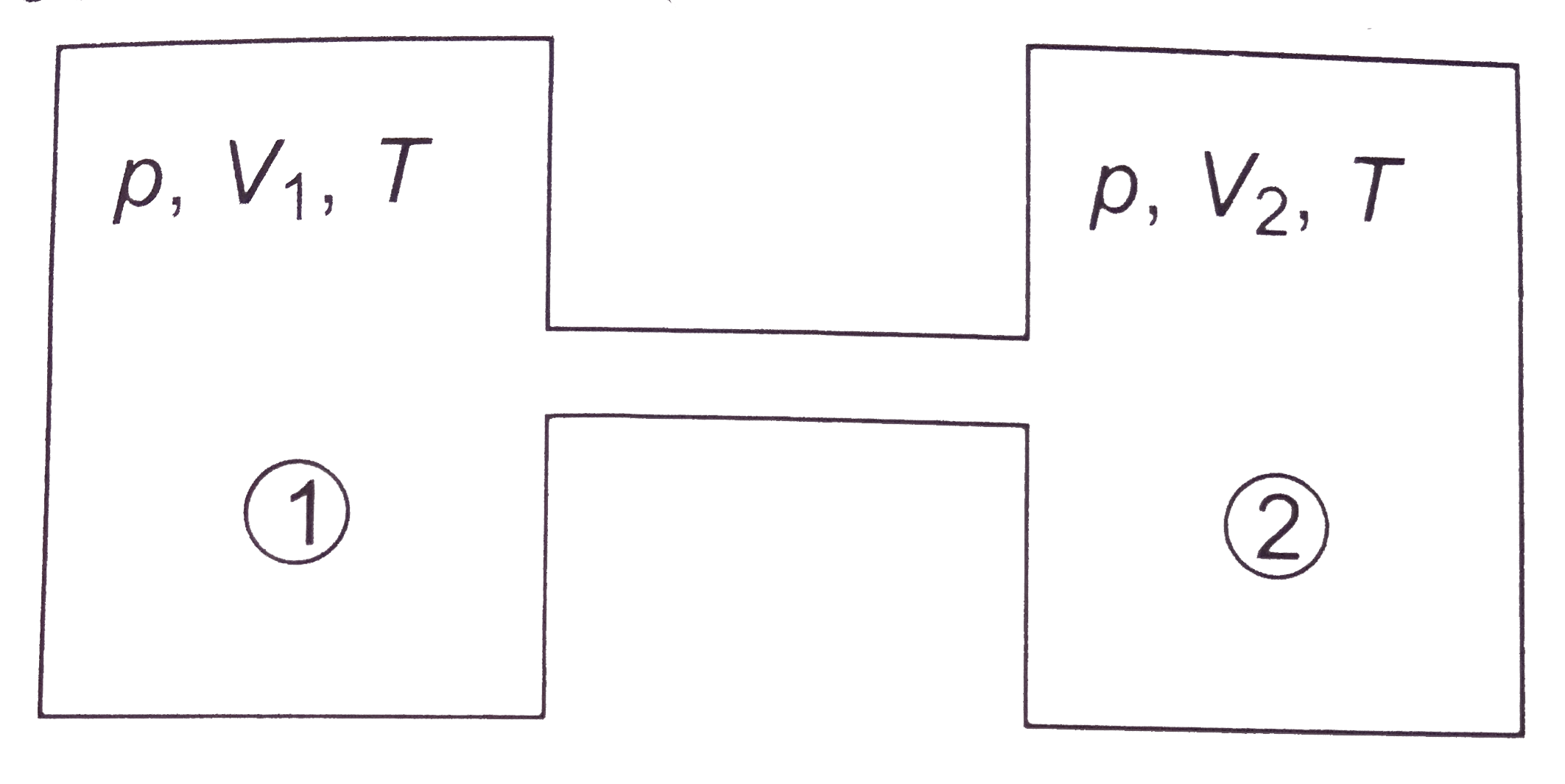
Since number of moles remains same
$n_{1} + n_{2} = n'_{1} + n'_{2}$
$\frac{p_{1} V_{1}}{R T_{1}} + \frac{p_{2} V_{2}}{R T_{2}} = \frac{p V_{1}}{R T} + \frac{p V_{2}}{R T}$
$\frac{p_{1} V_{1}}{T_{1}} + \frac{p_{2} V_{2}}{T_{2}} = \frac{p}{T} (V_{1} + V_{2})$ .(i)
Since vessel is insulated, total internal energy remains same
$U_{1} + U_{2} = U'_{1} + U'_{2}$
$n_{1} C_{V} T_{1} + n_{2} C_{V} T_{2} = n'_{1} C_{V} T + n'_{2} C_{V} T$
$\frac{p_{1} V_{1}}{R} + \frac{p_{2} V_{2}}{R} = \frac{p V_{1}}{R} + \frac{p V_{2}}{R}$
Common pressure: $p = \frac{p_{1} V_{1} + p 2 V_{2}}{V_{1} + V_{2}}$
Common temperature: $T = \frac{p (V_{1} + V_{2})}{\frac{p_{1} V_{1}}{T_{1}} + \frac{p_{2} V_{2}}{T_{2}}} = \frac{p_{1} V_{1} + p_{2} V_{2}}{\frac{p_{1} V_{1}}{T_{1}} + \frac{p_{2} V_{2}}{T_{2}}}$

Updated on:21/07/2023

Two thermally insulated vessel 1 and 2 are filled with air at temperature $(T_{1} T_{2}), v o l u m e (V_{1} V_{2})$ and pressure $(P_{1} P_{2})$ respectively. If the valve joining the two vessels is opened, the temperature inside the vessel at equilibrium will be
A $T_{1} T_{2} (P_{1} V_{1} + P_{2} V_{2}) / (P_{1} V_{1} T_{2} + P_{2} V_{2} T_{1})$
B $(T_{1} + T_{2}) / 2$
C $T_{1} + T_{2}$
D $T_{1} T_{2} (P_{1} V_{1} + P_{2} V_{2}) / (P_{1} V_{1} T_{1} + P_{2} V_{2} T_{2})$
$\frac{P_{1} V_{1}}{T_{1}} = \frac{P_{2} V_{2}}{T_{2}}$ is -
ABoyle's Law
BCombined gas law
CCharles Law
DNone of these
Two thermally insulated vessel 1 and 2 are filled with air at temperature $(T_{1} T_{2}), v o l u m e (V_{1} V_{2})$ and pressure $(P_{1} P_{2})$ respectively. If the valve joining the two vessels is opened, the temperature inside the vessel at equilibrium will be
A $T_{1} + T_{2}$
B $\frac{(T_{1} + T_{2})}{2}$
C $\frac{T_{1} T_{2} (P_{1} V_{1} + P_{2} V_{2})}{P_{1} V_{1} T_{2} + P_{2} V_{2} T_{1}}$
D $\frac{T_{1} T_{2} (P_{1} V_{1} + P_{2} V_{2})}{P_{1} V_{1} T_{1} + P_{2} V_{2} T_{2}}$