using the illustration when both surfaces 1 and 2 are exposed to the atmoshere, $P_{1}$ and $P_{2}$ are gauge pressure , and $h_{1}$ and $h_{2}$ are heights .

The Bernoulli equation for this situation is $h_{1} + \frac{P_{1}}{W} + \frac{V_{1}^{2}}{2a} = h_{2} + \frac{P_{2}}{W} + \frac{V_{2}^{2}}{2a}$
The value of $P_{1}$ and $P_{2}$ are such that

$P_{1} = P_{2} = 0$

$P_{2}$ lt $P_{1}$

$P_{1} > P_{2}$

$P_{1} / P_{2} = 0$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Updated on:21/07/2023

using the illustration when both surfaces 1 and 2 are exposed to the atmoshere, $P_{1}$ and $P_{2}$ are gauge pressure , and $h_{1}$ and $h_{2}$ are heights .

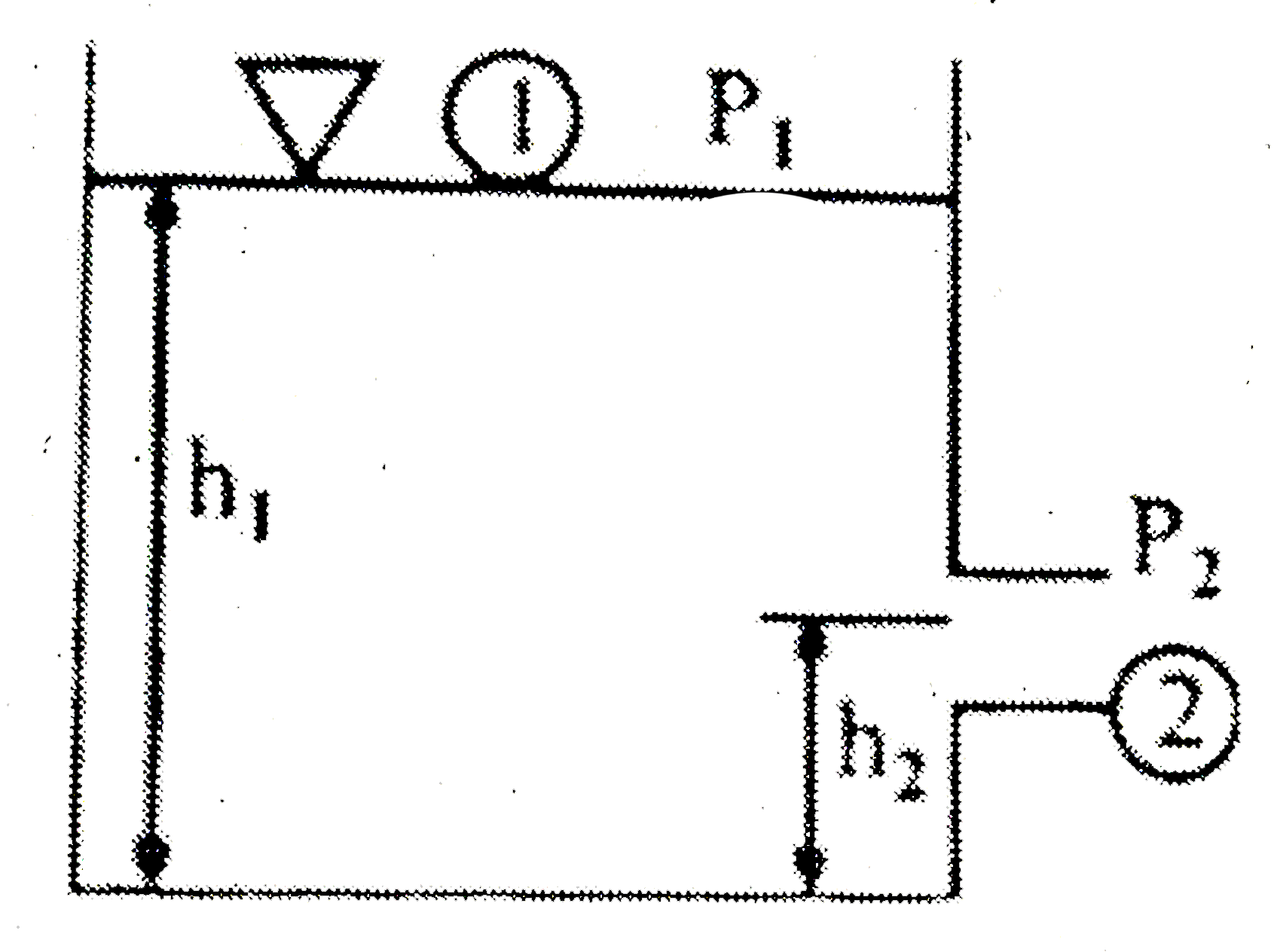
The Bernoulli equation for this situation is $h_{1} + \frac{P_{1}}{W} + \frac{V_{1}^{2}}{2a} = h_{2} + \frac{P_{2}}{W} + \frac{V_{2}^{2}}{2a}$
The velocity of the fluid leavening point (2) is constant and can be expressed as
A $V_{2} = (P_{1} / P_{2}) V_{1}$
B $V_{2} = (P_{1} / P_{2}) a h$
C $V_{2} = {[(h_{1} - h_{2}) (2 a)]}^{1 / 2}$
Dnone of the above
using the illustration when both surfaces 1 and 2 are exposed to the atmoshere, $P_{1}$ and $P_{2}$ are gauge pressure , and $h_{1}$ and $h_{2}$ are heights .

The Bernoulli equation for this situation is $h_{1} + \frac{P_{1}}{W} + \frac{V_{1}^{2}}{2a} = h_{2} + \frac{P_{2}}{W} + \frac{V_{2}^{2}}{2a}$
If an Identical outlet were placed at exactly the same point on the left side of the container, the velocity would be
Azero
Bcomputable
C $2 V_{2}$
Dnone of the above
The top surface of an incompressible liquid is open to the atmosphere. The pressure at a depth $h_{1}$ below the surface is $p_{1}$ . What is the pressure $p_{2}$ at depth $h_{2} = 2 h_{1}$ compare with $p_{1}$ ?
A $p_{2} > 2 p_{1}$
B $p_{2} = 2 p_{1}$
C $p_{2} < 2 p_{1}$
D $p_{2} = p_{1}$