A source of light of wavelength 5000Å is placed as shown in figure.
Considering interference of direct and reflected rays, determine the position of the
region where the fringes will be visible and calculate the number of fringes.
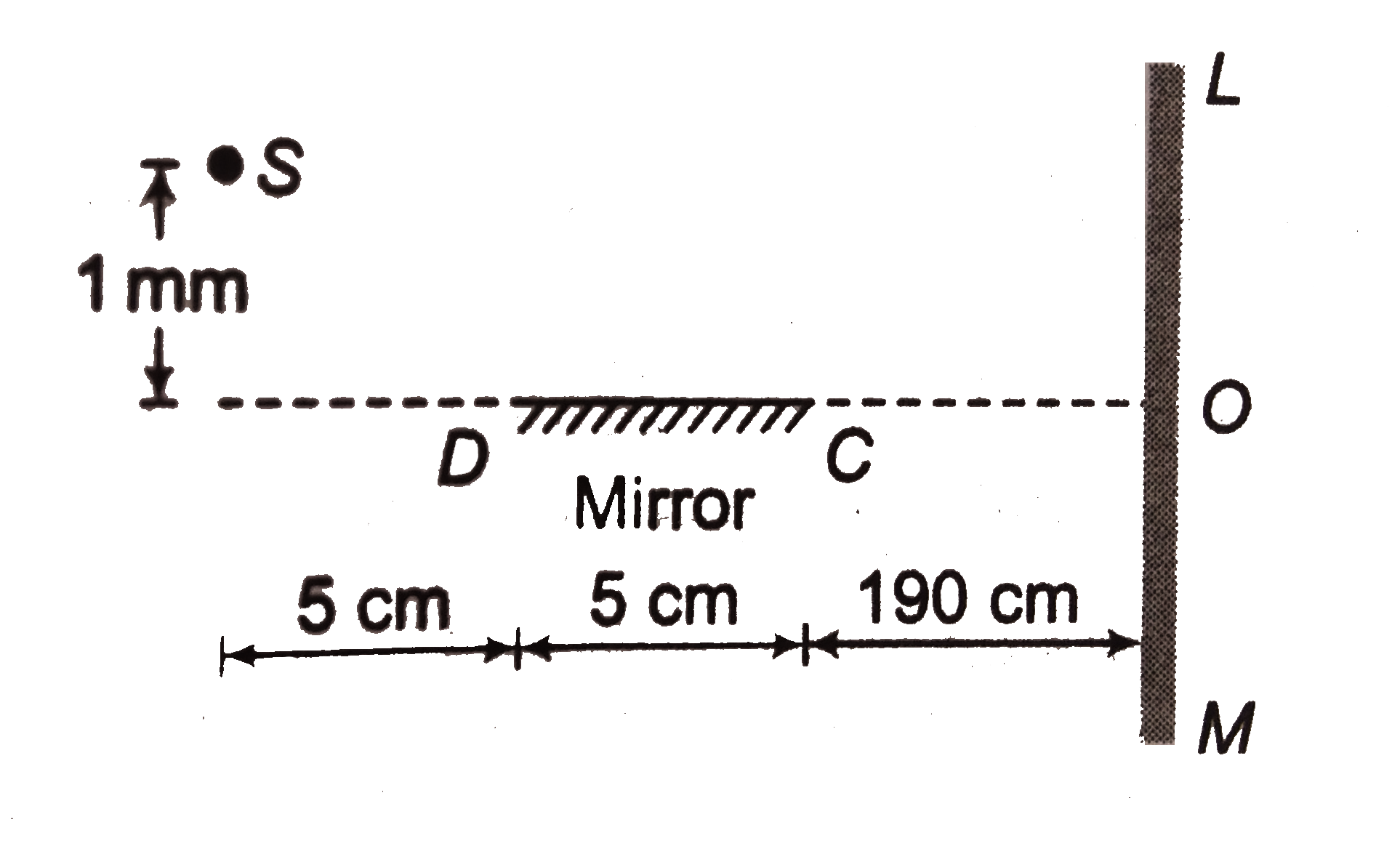 .
.
The correct Answer is:D
Interference will be obtained between
direct rays from S and reflected rays from S' (image
of S on mirror).
Since, the reflected rays will lie between region P and
Q on the screen. So, interference is obtained in this
region only. From geometry will can show that,
OP = 1.9cm and OQ = 3.9cm.
∴PQ=2cm
Fr∈≥wh,ω=λDd=(5000×10−8)(200)2×10−1cm=0.05cm
Total number of fringes in the region PQ,
N=PQω=20.05=40

Topper's Solved these Questions
- INTERFERENCE AND DIFFRACTION OF LIGHTBOOK - DC PANDEYCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - Example Type 5
1 Videos
- INTERFERENCE AND DIFFRACTION OF LIGHTBOOK - DC PANDEYCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - type-5
1 Videos
- INTERFERENCE AND DIFFRACTION OF LIGHTBOOK - DC PANDEYCHAPTER - INTERFERENCE AND DIFFRACTION OF LIGHTEXERCISE - type-3
1 Videos
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - All Questions
120 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEYCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery
59 Videos
Similar Questions
A source of light of wavelength 5000 Å is placed at one end of table 2 m long and 5 mm above its flat polished metal top. Find the fringe width of the interference bands are located on a screen at the end of the table .
View SolutionTwo monochromatic coherent sources of wavelength 5000 Å are placed along the line normal to the screen as shown in the figure.
(a) Determine the condition for maxima, at the point P.
(b)Find the order of the central bright fringe if d = 0.5 mm, D = 1 m.

View Solution
Knowledge Check
A point source of light is placed in front of a plane mirror as shown in Figure.
Determine the length of reflected path of light on the screen Σ
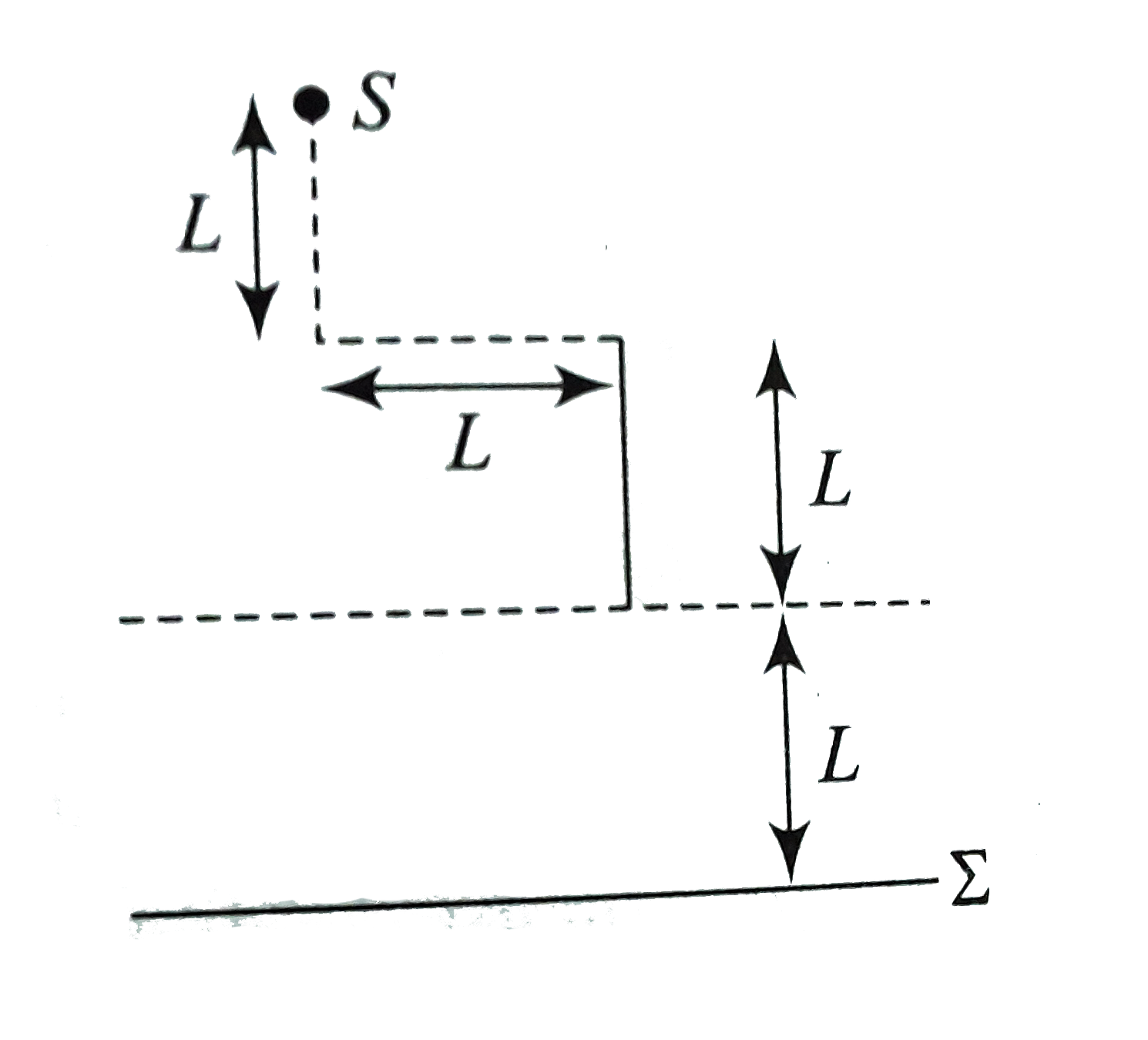 ALB2LC3L/2DL/2
ALB2LC3L/2DL/2Two sources of light of wavelength 4500 Å annd 6000 Å are used simultaneously in Young's double slit experiment. At which order of the two wavelength pattern,s the fringes coincide?
A3rd orders of both λ1andλ2B4th orders of both λ1andλ2C4th order of λ1=4500 Å and 3rd order of λ2=6000 ÅD3rd order of λ1=4500 Å and 4th order of λ2=6000 ÅIn Young's experiment when sodium light of wavelength 5893Å is used, then 62 fringes are seen in the field of view. Instead if violet light of wavelength 4358Å is used then the number of fringes trhat will be seen in the field of view will be
A54B64C74D84
A beam of light consisting of two wavelengths, 6500 Å and 5200Å , is used, to obtain, interference fringes in a Young’s double slit experiment
Q(a) Find the distance of the third bright fringe on the screen from the central maximum for wavelength 6500 Å
.) What is the least distance form the central maximum where the bright fringes due to both wavelengths coincide?
The distance between the slits is 2 mm and the distance between the plane of slits and p the screen is 120 cm.
View SolutionA point sources S emitting light of wavelength 600nm is placed at a very small height h above the flat reflecting surface AB(see figure).The intensity of the reflected light is36% of the intensity.interference firnges are observed on a screen placed parallel to the reflecting surface a very large distance D from it.
(A)What is the shape of the interference fringes on the screen?
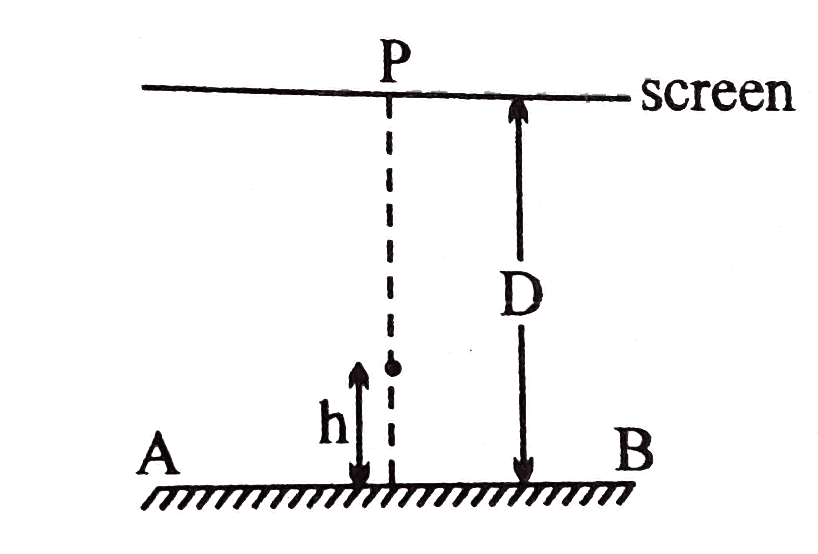
(B)Calculate the ratio of the minimum to the maximum to the maximum intensities in the interference fringes fromed near the point P (shown in the figure) (c) if the intenstities at point P corresponds to a maximum,calculate the minimum distance through which the reflecting surface AB should be shifted so that the intensity at P again becomes maximum.
View SolutionLight of wavelength 6000Å is reflected at nearly normal incidence from a soap films of refractive index 1.4 The least thickness of the fringe then will appear black is
View SolutionLight of wavelength 5000 Å, illuminates the slit in a biprism experiment. If it is replaced by light of wavelength 6500 Å, then the fringe width will
View SolutionA monochromatic light beam of wavelength 5896Å is used in double slit experiment to get interference patter on a screen. 9th bright fringe is seen at a particular position on the screen. At the same point on the screen. If 11th bright fringe is to be seen, the wave length of the light that is needed is (nearly)
View Solution
