Consider the situation shown in figure. The two slite $S_{1} and S_{2}$
placed symmetrically around the centre line are illuminated by a monochromatic
light of wavelength lambda. The separation between the slits is d. The light transmitted
by the slits falls on a screen $M_{1}$ placed at a distance D from the slits. The slit $S_{3}$ is
at the centre line and the slit $S_{4}$ is at a distance y form $S_{3}$ . Another screen $M_{2}$ is
placed at a further distance D away from $M_{1}$ . Find the ration of the maximum to
minimum intensity observed on $M_{2}$ if y is equal to $(d < < D)$ .
$< i m g a \leq ocr_image l o a d \in g = lazy s r c = https://d10lpgp6xz60nq.cloudfront.net/physics_images/ DCP_V05_C32_S01_022_Q01.png w h = 80% mx-auto s t y \leq = background:white; > < b r >$ (a) (lambdaD)/(2d) (b)(lambdaD)/d (c) (lambdaD)/(4d)

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A, B, C, D

$S_{1} S_{3} = S_{2} S_{3}$
$∴ Δ x at S_{3}$ is zero. Therefore, intensity at $S_{3}$ will be $4 I_{0}$ . Let us call it $I_{1}$ . Thus,
$I_{S_{3}} = I_{1} = 4 I_{0}$
Now, $I_{S_{4}}$ (or $I_{2})$ depends on the value of y.
(a) When y= $\frac{λ D}{2 d}$
$Δ x = \frac{y d}{D} = \frac{λ}{2}$
$∴ I_{S_{4}} = I_{2} = 0$
or $\frac{I_{max}}{I_{min}} = {(\frac{{\sqrt{I}}_{1} + {\sqrt{I}}_{2}}{{\sqrt{I}}_{1} - {\sqrt{I}}_{2}})}^{2} = 1$
$(b) W h e n y = \frac{λ D}{d}$
$Δ x = \frac{y d}{D} = λ$
$∴ I_{S_{4}} = I_{2} = 4 I_{0}$
or $\frac{I_{max}}{I_{min}} = {⎛ ⎝ \frac{{\sqrt{I}}_{1} + {\sqrt{I}}_{2}}{{\sqrt{I}}_{1} - \sqrt{_} (2)} ⎞ ⎠}^{2} = \infty$
( c) When $y = \frac{λ D}{4 d}$
$\Rightarrow Δ ϕ = \frac{y d}{D} = \frac{λ}{4}$
$∴ I_{S_{4}} = I_{2} = 4 I_{0} ({cos}^{2}) \frac{ϕ}{2} = 2 I_{0}$
or $\frac{I_{max}}{I_{min}} = ⎛ ⎝ {(\frac{{\sqrt{I}}_{1} + {\sqrt{I}}_{2}}{{\sqrt{I}}_{1} - {\sqrt{I}}_{2}})}^{2} = 34$ .

Updated on:21/07/2023

Class 12 PHYSICS WAVE OPTICS

Topper's Solved these Questions

Knowledge Check

Consider the situation shown in fig. The two slits $S_{1}$ and $S_{2}$ placed symmetrically around the central line are illuminated by monochromatic light of wavelength $λ$ . The separation between the slit is d. The ligth transmitted by the slits falls on a screen $S_{0}$ placed at a distance D form the slits. The slit $S_{3}$ is at the central line and the slit $S_{4}$ is at a distance z from $S_{3}$ Another screen $S_{c}$ is placed a further distance D away from $S_{c}$ Find the ratio of the maximum to minimum intensity observed on $S_{c}$

If $z = \frac{λ D}{4 d}$
A ${[3 - 2 \sqrt{2}]}^{2}$
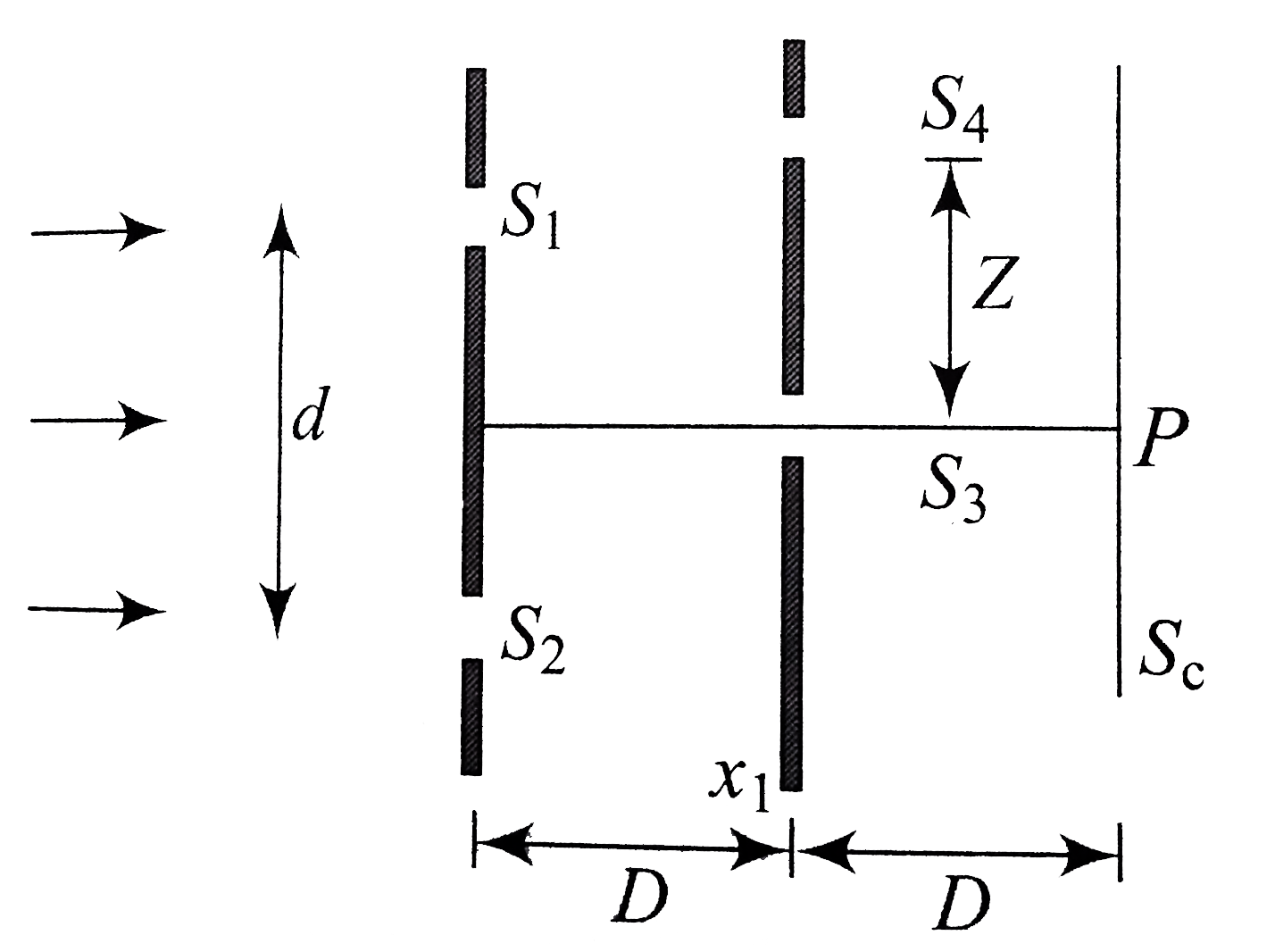
B ${[3 + \sqrt{2}]}^{2}$
C ${[3 - \sqrt{2}]}^{2}$
D ${[3 + 2 \sqrt{2}]}^{2}$
Consider the situation shown in fig. The two slits $S_{1}$ and $S_{2}$ placed symmetrically around the central line are illuminated by monochromatic light of wavelength $λ$ . The separation between the slit is d. The ligth transmitted by the slits falls on a screen $S_{0}$ placed at a distance D form the slits. The slit $S_{3}$ is at the central line and the slit $S_{4}$ is at a distance z from $S_{3}$ Another screen $S_{c}$ is placed a further distance D away from $S_{c}$ Find the ratio of the maximum to minimum intensity observed on $S_{c}$

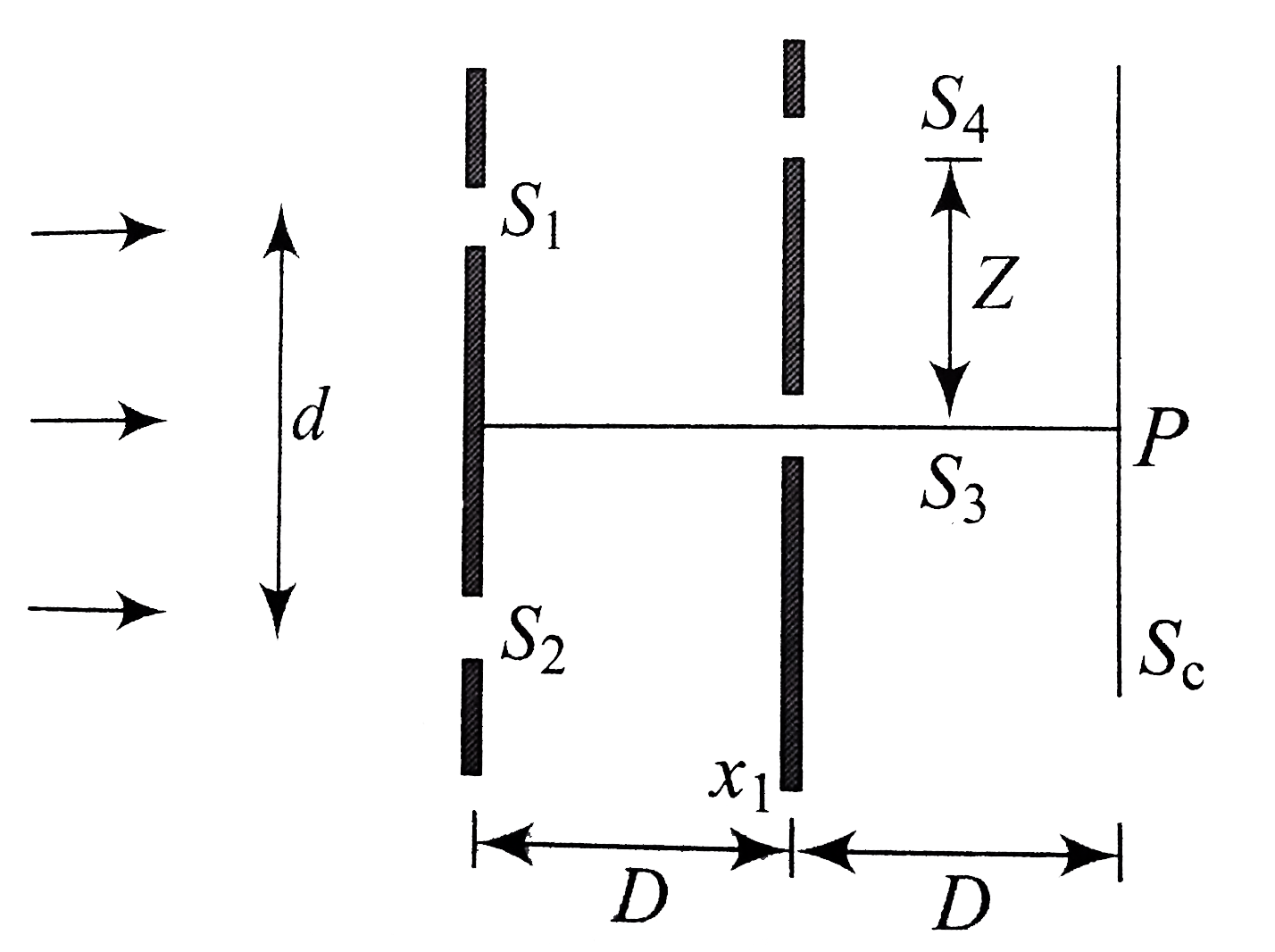
If $z = \frac{λ D}{2 d}$
A1
B $1 / 2$
C $3 / 2$
D2
Consider the situation shown in fig. The two slits $S_{1}$ and $S_{2}$ placed symmetrically around the central line are illuminated by monochromatic light of wavelength $λ$ . The separation between the slit is d. The ligth transmitted by the slits falls on a screen $S_{0}$ placed at a distance D form the slits. The slit $S_{3}$ is at the central line and the slit $S_{4}$ is at a distance z from $S_{3}$ Another screen $S_{c}$ is placed a further distance D away from $S_{c}$ Find the ratio of the maximum to minimum intensity observed on $S_{c}$

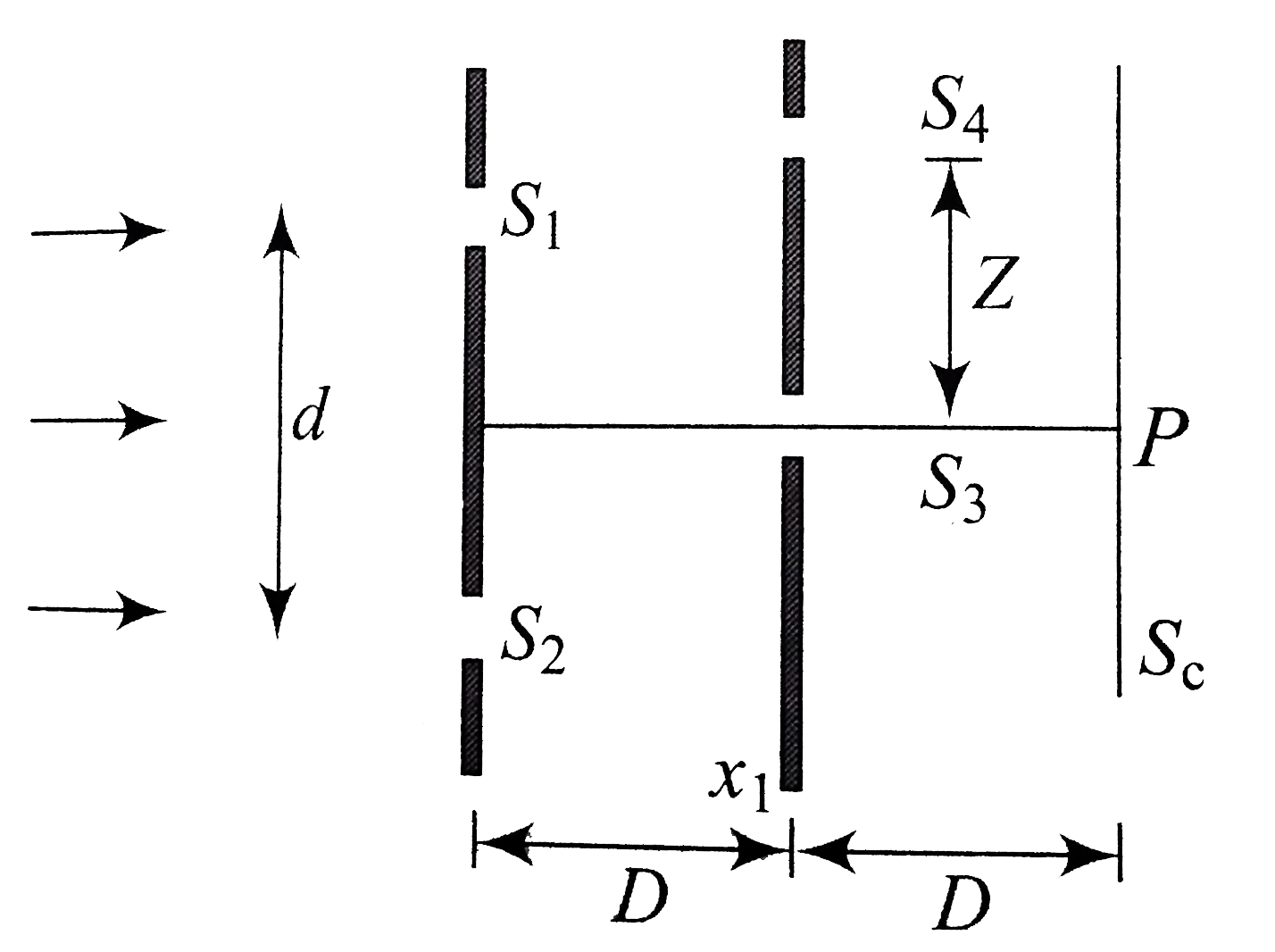
If $z = \frac{λ D}{d}$
A4
B2
C $\infty$
D1

DC PANDEY-INTERFERENCE AND DIFFRACTION OF LIGHT-Example Type 5

Consider the situation shown in figure. The two slite S1 and S2 plac...
09:36

The correct Answer is:A, B, C, D

Topper's Solved these Questions

Similar Questions

Knowledge Check

DC PANDEY-INTERFERENCE AND DIFFRACTION OF LIGHT-Example Type 5