A convex lens of focal length 1.5m is placed in a system of coordinate axis such that its optical centre is at origin and principa, axis coinciding with the x-axis. An object and a plane mirror are arrange on theh principal axis as shown in figure. Find value of d (in m) so that y-coordinate of image (after refraction and reflection ) is 0.3m. (Take
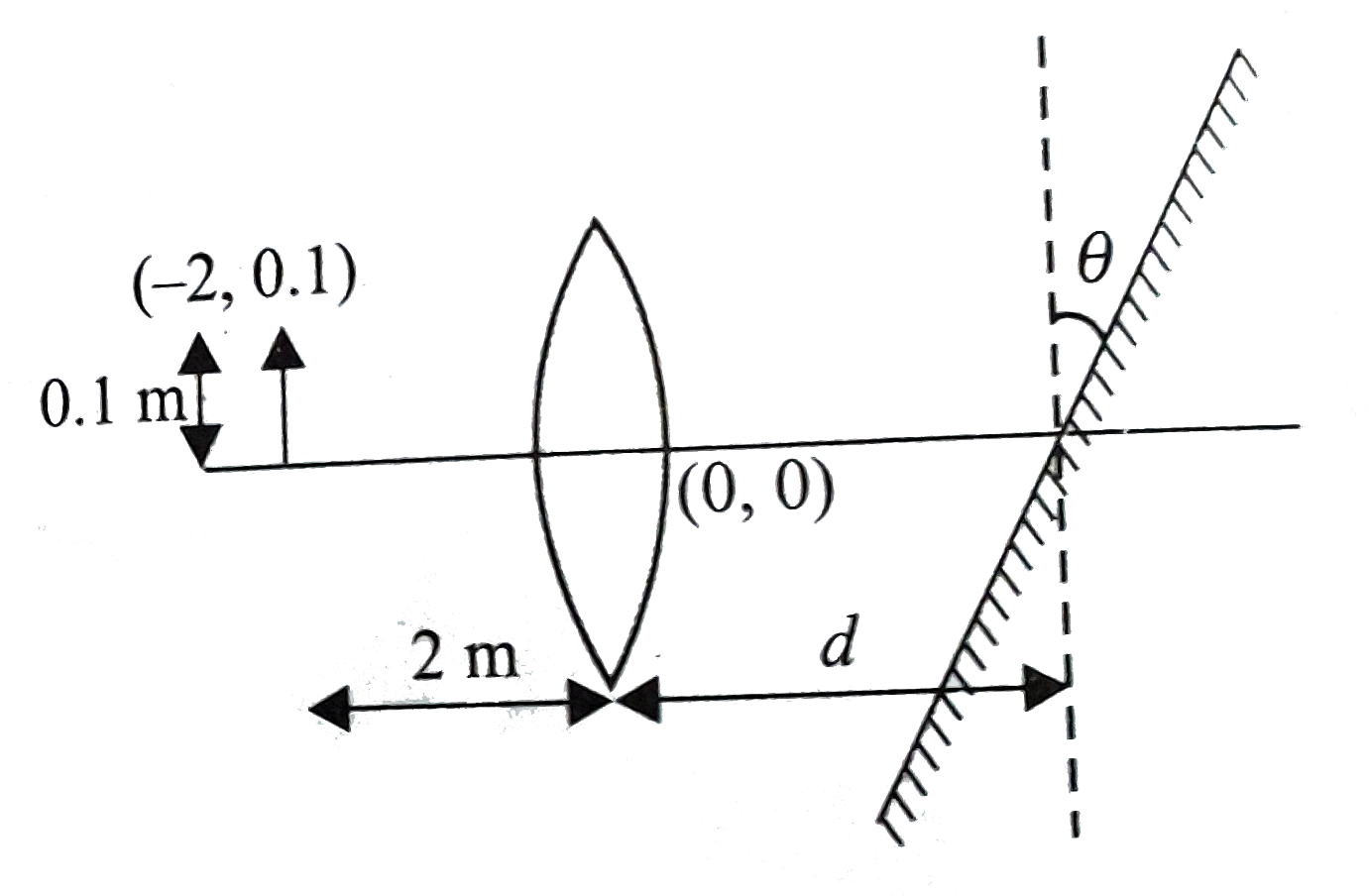
The correct Answer is:A, C, D
Step by step video, text & image solution for A convex lens of focal length 1.5m is placed in a system of coordinate axis such that its optical centre is at origin and principa, axis coinciding with the x-axis. An object and a plane mirror are arrange on theh principal axis as shown in figure. Find value of d (in m) so that y-coordinate of image (after refraction and reflection ) is 0.3m. (Take tan theta=0.3) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A concave lens of focal length 20 cm is placed 15 cm in front of a concave mirror of radius of curvature 26 cm and further 10 cm away from the lens is placed an object. The principal axis of the lens and the mirror are coincident and the object is on the axis Find the position and nature of the image.
View SolutionA convex lens is placed in contact with a plane mirror. An axial point object at a distance of 20cm from this combination, has its image coinciding with itself. What is the focal length of the convex lens ?
View Solution
Knowledge Check
A lens is placed in the XYZcoordinate system such that its optical center is at the original and principal axis is along the X axis.The focal length of the lens is20cm.A point object has been placed at the point (−40cm,61cm−1cm)Which of the following are correct about coordiantes of the image?
Ax=40cmBy=+1cmCz=+1cmDz=−1cm
Two plane mirrors intersect at origin. An object 'O' is kept at a distance R on negative y-axis as shown in the figure. The co-ordinates of images formed after three reflections will be (first reflection is is considered at m1)A(−R/2,+√3R/2)(−R,0)&(+√3R/2,+R/2)B(−√3R/2,+R/2)(+R,0)&(+R√2,+R√2)C(√3R/2)(−R,0)&(+R/2,+√3R/2)D(−R√2,R√2)(+R,0)&(+R2,+√3R2)A convex lens of focal length 15 cm is placed in front of a plane mirror at a distance 25 cm from the mirror. Where on the optical axis and from the centre of the lens should a small object be placed such that the final image coincides with the object ?
A15 cm and on the opposite side of the mirrorB15 cm and between the mirror and the lensC7.5 cm and on the opposite side of the mirrorD7.5 cm and between the mirror and the lens
A convex lens is placed in contact with a plane mirror. A point object at a distance of 20 cm on the axis of this combination has its image coinciding with itself. What is the focal length of the lens ?
View SolutionA convex lens of focal length 15cm is placed in front of a convex mirror. Both are coaxial and the lens is 5cm from the apex of the mirror. When an object is placed on the axis at a distance of 20cm from the lens, its is found that image coincides with the object. Calculate the radius of curvature of mirror.
[55cm]
View SolutionA thin convex lens of focal length 25cm is cut into two pieces 0.5cm above the principal axis. The top part is placed at (0.0) and an object placed at (−50cm,0). Find the coordinates of the image.
View SolutionA thin convex lens of focal length 30cm is placed in front of a plane mirror. An object is placed at a distance x from the lens (not in between lens and mirror ) so that its final image coincides with itself. Then, the value of x is
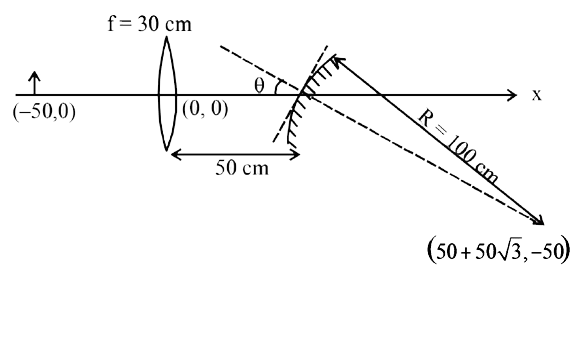
View SolutionA small object is placed 50 cm to the left of a thin convex lens of focal length 30 cm. A convex spherical mirror of radius of curvature 100 cm is placed to the right of the lens at a distance of 50 cm. The mirror is tilted such that the axis of the mirror is at an angle θ=30degree to the axis of the lens, as shown in the figure
If the origin of the coordinate system is taken to be at the centre of the lens, the coordinates (in cm) of the point (x,y) at which the image is formed are
View Solution
