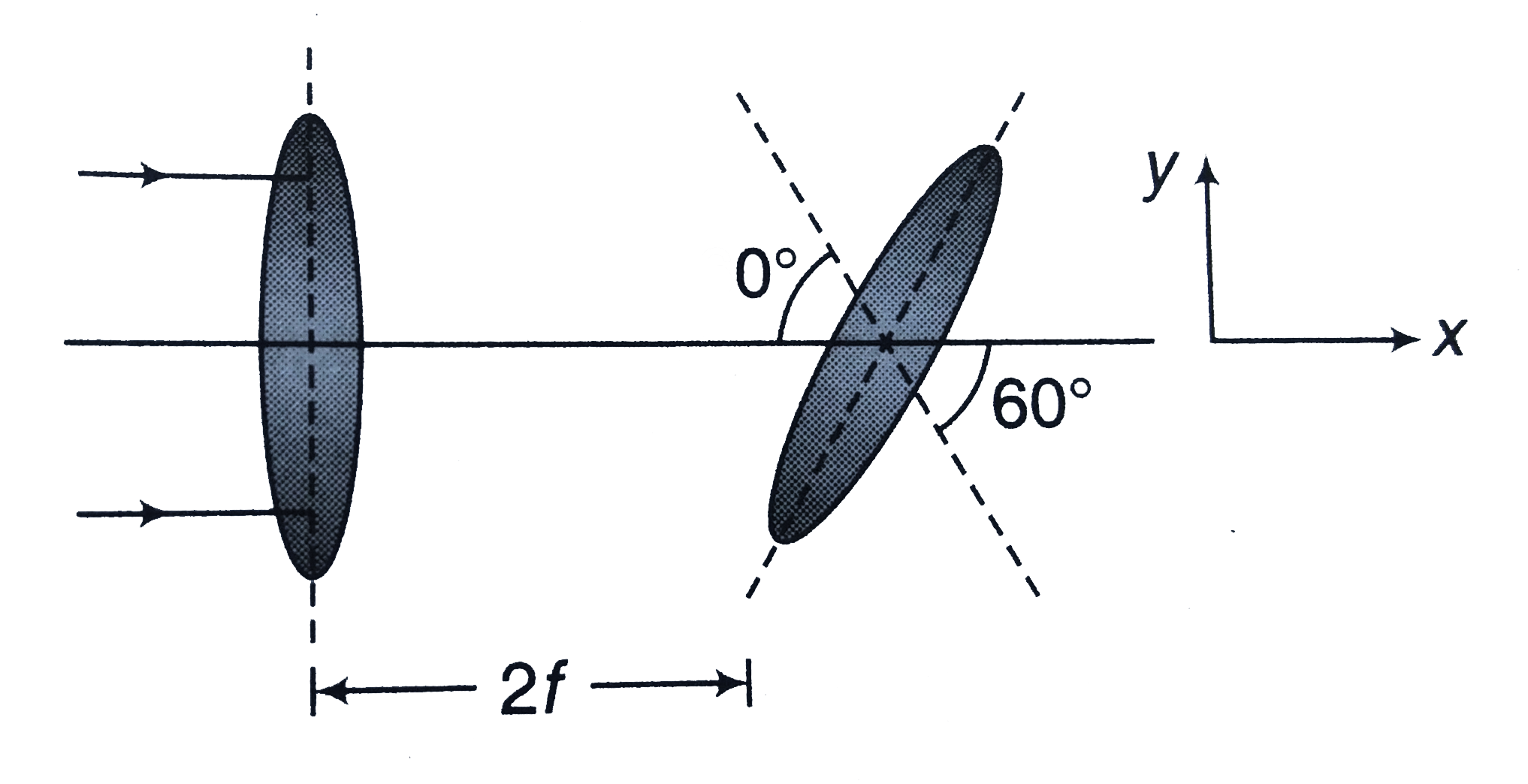
Two converging lenses of the same focal length f are separated by a distance 2f. The axis of the second lens is inclined at angle θ=60∘ with respect to the axis of the first lens. A parallel paraxial beam of light is incident from left side of the lens. Find the coordinates of the final image with respect to the origin of the first lens.
Using lens formula for L2,
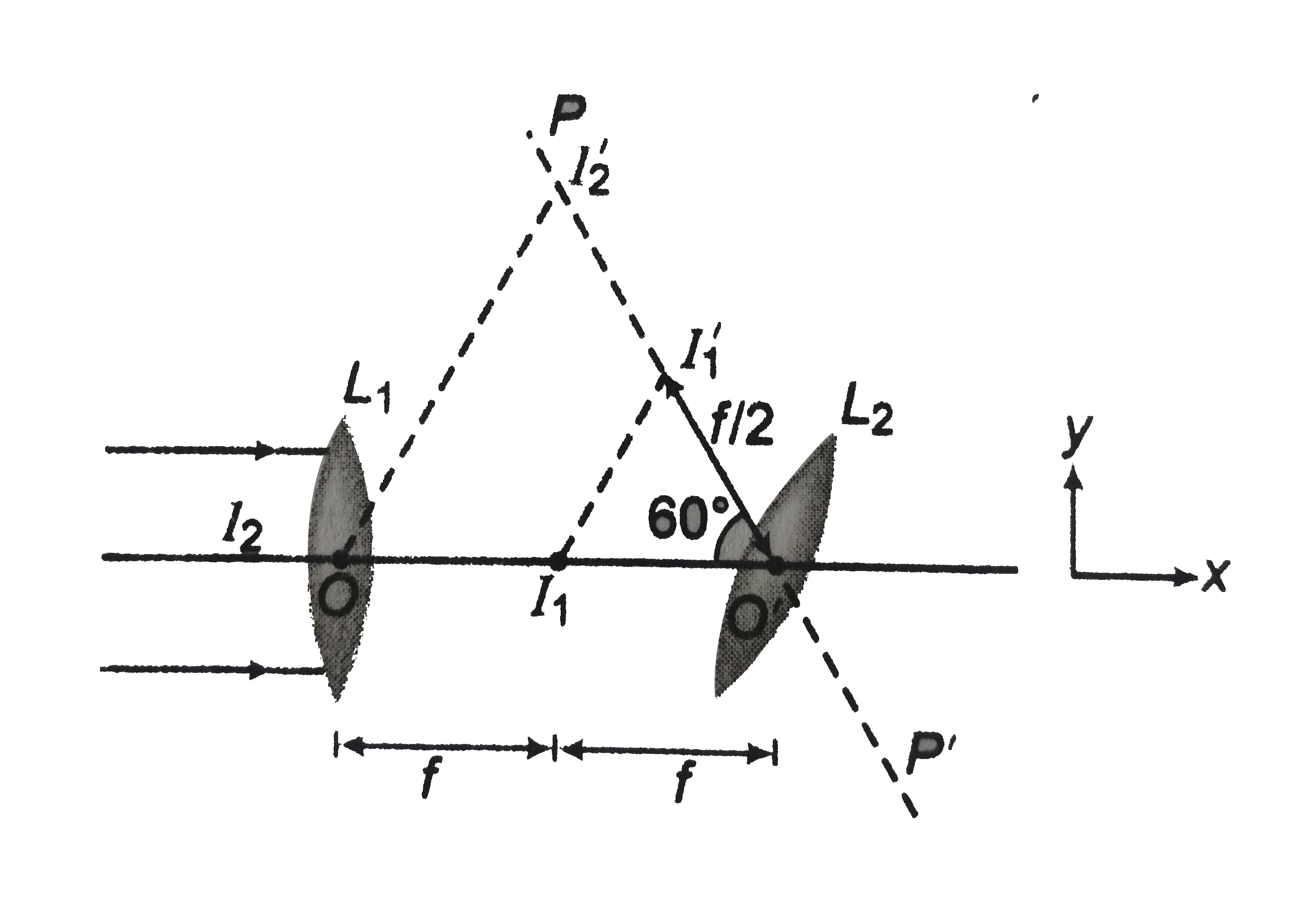
1v−1−f/2=1f
or v=−f
This f length will be along PP' from point O'
(towards P).
∴O'I2'=f
On x-axis this distance will be f sec60∘=2f.
Since, OO'=2f, image will be formed at
origin.
Therefore I1andI2 both should be on this line,
which is also the x-axis. That's why for final
image we have taken projection of OI2' on x-axis.
Topper's Solved these Questions
Similar Questions
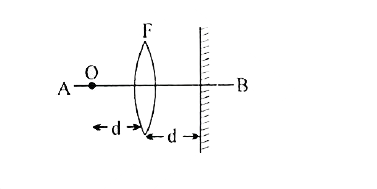
In the figure shown ‘O’ is point object. AB is principal axis of the converging lens of focal length F. Find the distance of the final image from the lens.
View SolutionA parallel beam of light is incident on a lens of focal length 10 cm. A parallel slab of refractive index 1.5 and thickness 3 cm is placed on the other side of the lens. Find the distance of the final image from the lens.
 .
.
View Solution
Knowledge Check
If the optic axis of convex and concave lenses are separated by a distance 5mm as shown in the figure. Find the coordinate of the final image formed by the combination if parallel beam of light is incident on lens. Origin is at the optical centre of convex lens
 A(25cm,0.5cm)B(25cm,0.25cm)C(25cm,−0.5cm)D(25cm,−2.5cm)
A(25cm,0.5cm)B(25cm,0.25cm)C(25cm,−0.5cm)D(25cm,−2.5cm)A convex lens and a concave lens, each of focal length 10 cm, are kept separated by a distance of 2 cm as shown in the figure. If the light is incident from left, the combination of lenses will be :
 AconvergingBdivergingCbehaving like a glass slabDconverging or diverging depending on whether the lenes are arranged as shwon in the figure on in the reverse order.
AconvergingBdivergingCbehaving like a glass slabDconverging or diverging depending on whether the lenes are arranged as shwon in the figure on in the reverse order.A convex lens of focal length f produces an image 1/n times the size of the object. The distance of the object from the lens is
A(n+1)fB(n−1)fCnfDfn
A glass wedge with a small angle of refraction θ is placed at a certain distance from a converging lens with a focal length f ,one surface of the wedge being perpendicular to the optical axis of the lens. A point sources S of light is on the other side of the lens at its focus. The rays reflected from the wedge (not from base) produce, after refraction in the lens , two images of the source displaced with respect to each other by d. Find the refractive index of the wedge glass. [Consider only paraxial rays.]
_E01_162_Q01.png)
View SolutionImage formation by a system of thin prism and lens
A beam parallel to the principal axis is incident on a thin prism (Fig. 34-60). Find the location of final image.
View SolutionTwo convex lenses of focal lengths f1andf2 are placed coaxially, a distance d apart. If the axis of one of the lenses is lifted parallel to itself by Δ, find the distance by which the focal point is shifted and the distance of the focal point from the first lens.
View SolutionTwo converging lenses of focal lengths f1=10cm and f2=20cm are placed at some separation. A parallel beam of light is incident on first lens. Then,
View SolutionA convex lens of focal length f produces an image 1/n times the size of the object. The distance of the object from the lens is
View Solution