If an object is placed at A(OA>f), where f is the focal length of the lens, the image is formed at B. A perpendicular is erected at O and C is chosen on it such that the angle (∠BCA) is a right angle. Then, the value of f will be 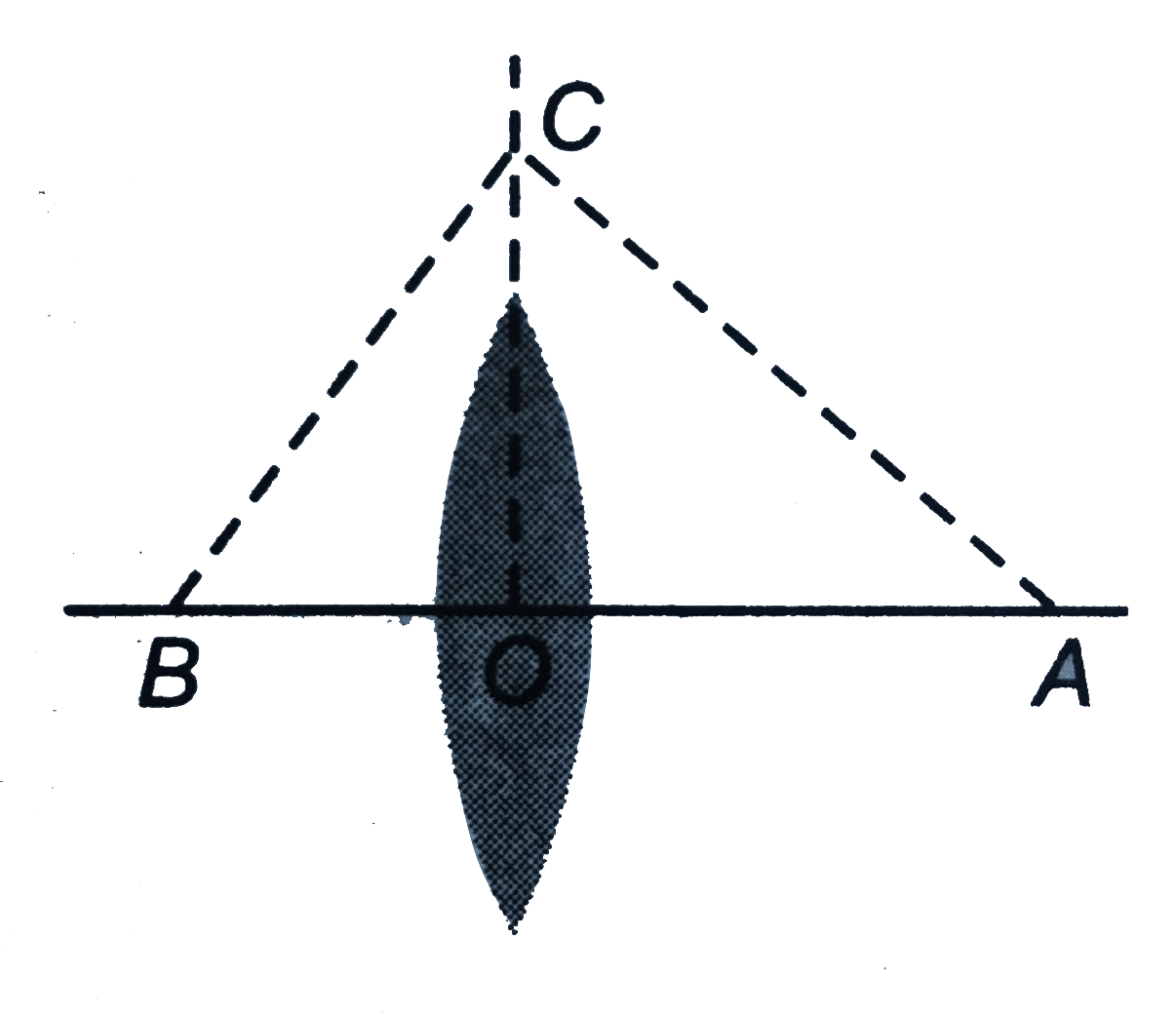
ABOC2
(AC)(BC)OC
OC2AB
(OC)(AB)AC+BC
The correct Answer is:C
1f=1OB−1−OA=1OB+1OA
f=(OA)(OB)AB+OB
∴f=(OA)(OB)AB….(i)
Now, AB2=AC2+BC2
or (OA+OB)2=AC2+BC2
or OA2+OB2+2(OA)(OB)=AC2+BC2
∴(AC2−OC2)+(BC2−OC2)
+2(OA)(OB)=AC2+BC2
Solving, we get
(OA)(OB)=OC2
Substituting in Eq. (i), we get
f=OC2AB
Topper's Solved these Questions
- REFRACTION OF LIGHTBook:DC PANDEYChapter:REFRACTION OF LIGHTExercise:Single Correct Option
Explore 3 Videos
- REFRACTION OF LIGHTBook:DC PANDEYChapter:REFRACTION OF LIGHTExercise:more than one correct option
Explore 1 Video
- REFRACTION OF LIGHTBook:DC PANDEYChapter:REFRACTION OF LIGHTExercise:Subjective Questions
Explore 8 Videos
- REFLECTION OF LIGHTBook:DC PANDEYChapter:REFLECTION OF LIGHTExercise:Subjective
Explore 9 Videos
- SEMICONDUCTORSBook:DC PANDEYChapter:SEMICONDUCTORSExercise:Subjective
Explore 12 Videos
Similar Questions
Knowledge Check
An object is placed at A(OA>f). Here, f is the focal length of the lens. The image is formed at B. A perpendicular is erected at O and C is chosen such that ∠BCA=90∘. Let OA = a, OB = b and OC = c. Then the value of f is
A(a+b)3c2B(a+b)c(a+c)Cc2a+bDa2a+b+cWhen an object is placed between O and F1 in front of a convex lens, the image formed
Aenlarged and erectBdiminished and erectCreal and enlargedDdiminished and invertedWhen an object is placed between O and F1 in front of a convex lens, the image formed
Aenlarged and erectBdiminished and erectCreal and enlargedDdiminished and inverted
An object is placed at a distance of 30 cm from a convex lens of focal length 20 cm.Is the image erect or inverted ?
View SolutionA object is placed 20 cm from the convex lens, with focal length 40 cm. The image formed is virtual and erect.
What will be power of the lens?
View SolutionAn object is placed at f/2 away from first focus of a convex lens where f is the focal length of the lens. Its image is formed at a distance 3f/2 in a slab of refractive index 3/2 , from the face of the slab facing the lens. Find the distance of this face of the slab from the second focus of the lens.
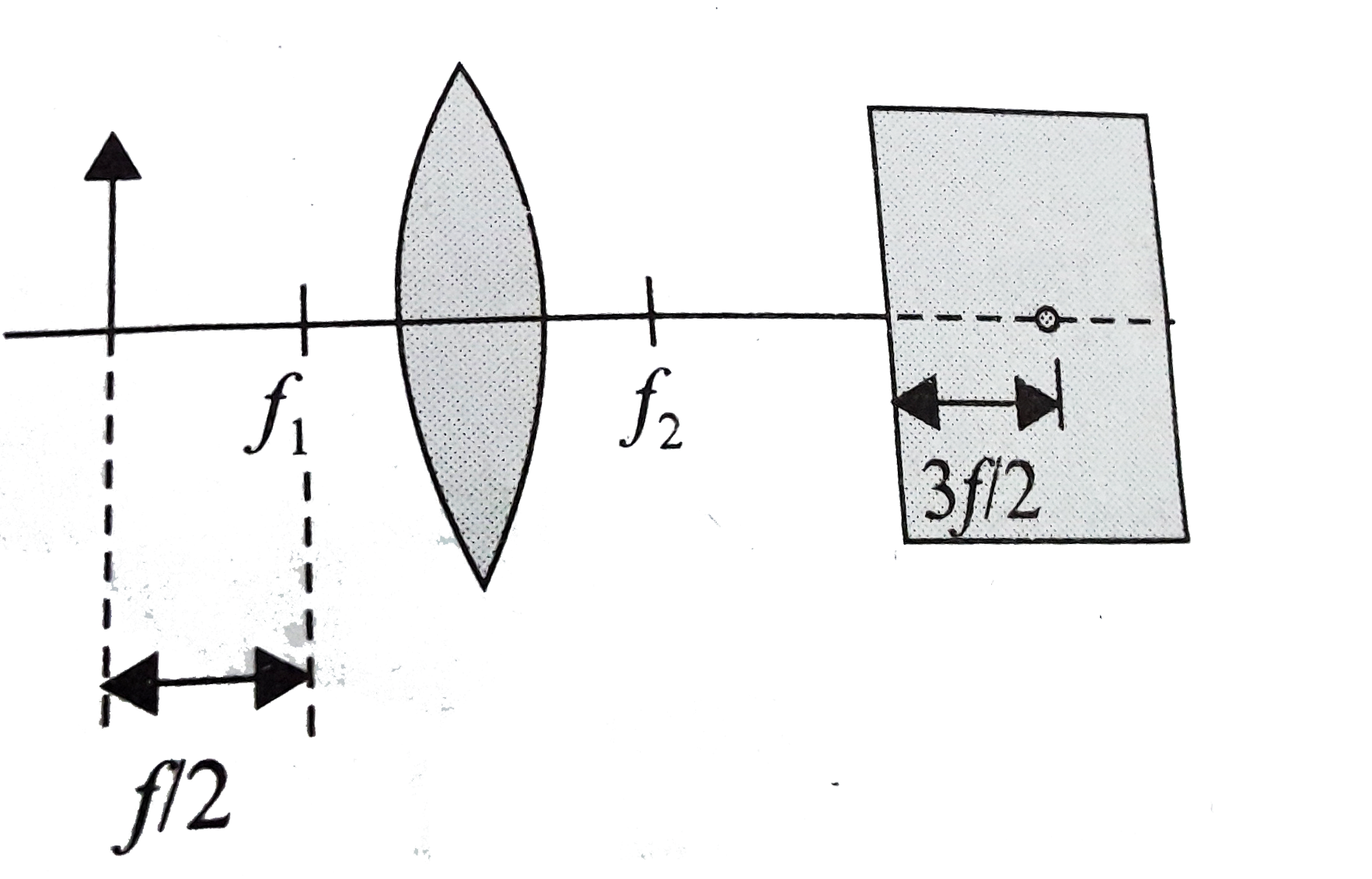
View SolutionAn object 25cmhigh is placed in front of a concave lens of focal length 30cm.If the height of image fromed is 50cm
if the image is erect and virtual then distance between object and image is
View SolutionA point object is placed on the optic axis of a convex lens of focal length f at a distance of 2f to the left of it. the diameter of the lens is 'd' . An eye is placed at a distance of 3f to the right of the lens and a distance h below the optic axis. The maximum value of h to see the image is
View Solution
