A cubical block of glass of refractive index n1 is in contact with the surface of water of refractive index n2. A beam of light is incident on vertical face of the block. After refraction a total internal reflection at the base and refraction at the opposite face take place. The ray emerges at angle θ as shown. The value of θ is given by

sinθ<√n21−n22
cosθ<√n21−n22
sinθ<1√n21−n22
cosθ<1√n21−n22
The correct Answer is:A
Applying Snell's law at point M, we get
n1=sinθsin(90∘−θC)orsinθ=n1cosθC
=n1√1−sin2θC=n1
⎷1−n22n21=√n21−n22
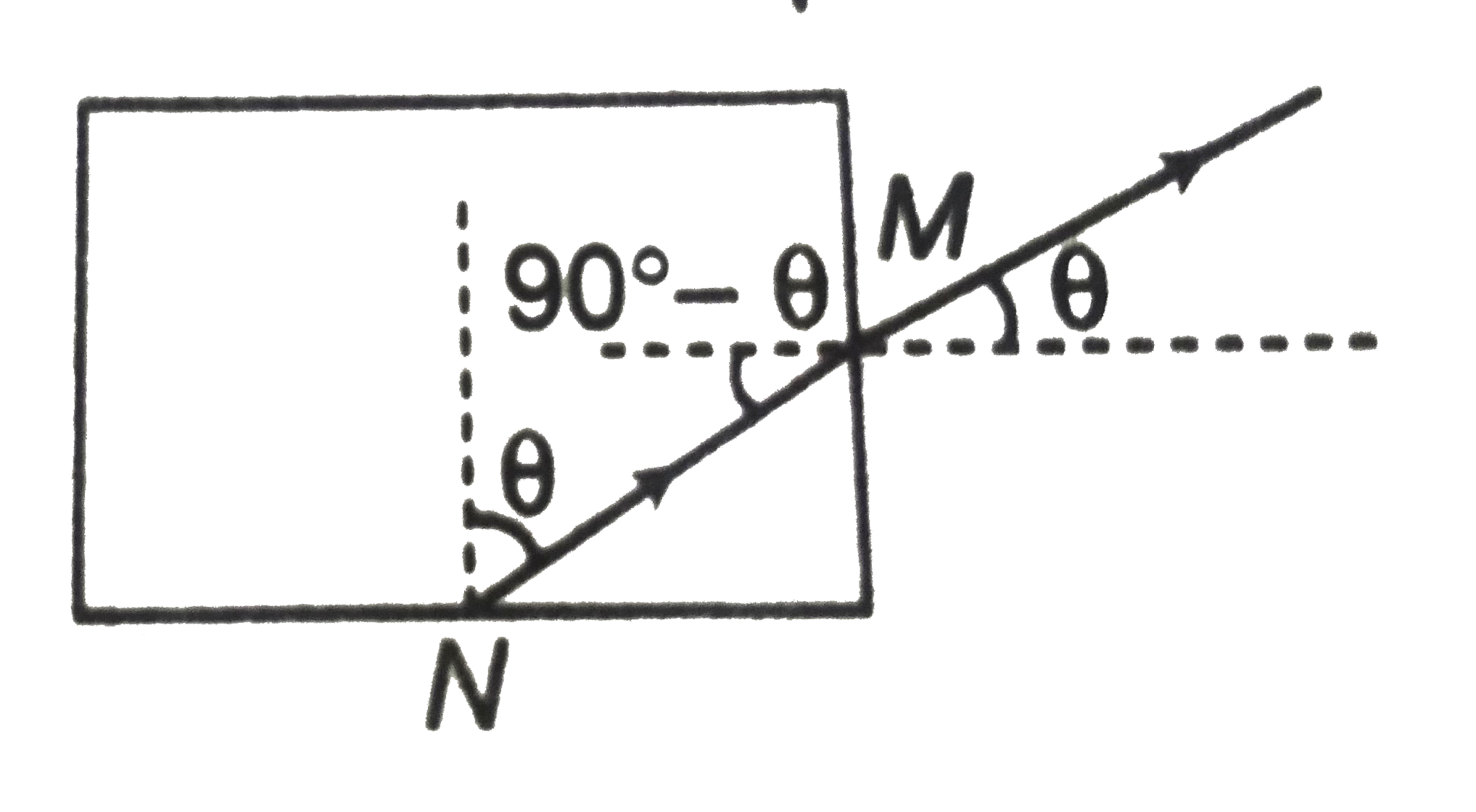
If angle of θ is less than this value, then angle of
incidence at N will be greater than θC. Hence , TIR
will take place at N.
Topper's Solved these Questions
- REFRACTION OF LIGHTBOOK - DC PANDEYCHAPTER - REFRACTION OF LIGHTEXERCISE - Single Correct Option
3 Videos
- REFRACTION OF LIGHTBOOK - DC PANDEYCHAPTER - REFRACTION OF LIGHTEXERCISE - more than one correct option
1 Videos
- REFRACTION OF LIGHTBOOK - DC PANDEYCHAPTER - REFRACTION OF LIGHTEXERCISE - Subjective Questions
8 Videos
- REFLECTION OF LIGHTBOOK - DC PANDEYCHAPTER - REFLECTION OF LIGHTEXERCISE - Subjective
9 Videos
- SEMICONDUCTORSBOOK - DC PANDEYCHAPTER - SEMICONDUCTORSEXERCISE - Subjective
12 Videos
Similar Questions
A ray of light is incident on the surface of a glass plate of index of refraction 1.55 at the polarizing angle. Calculate the angle of refraction.
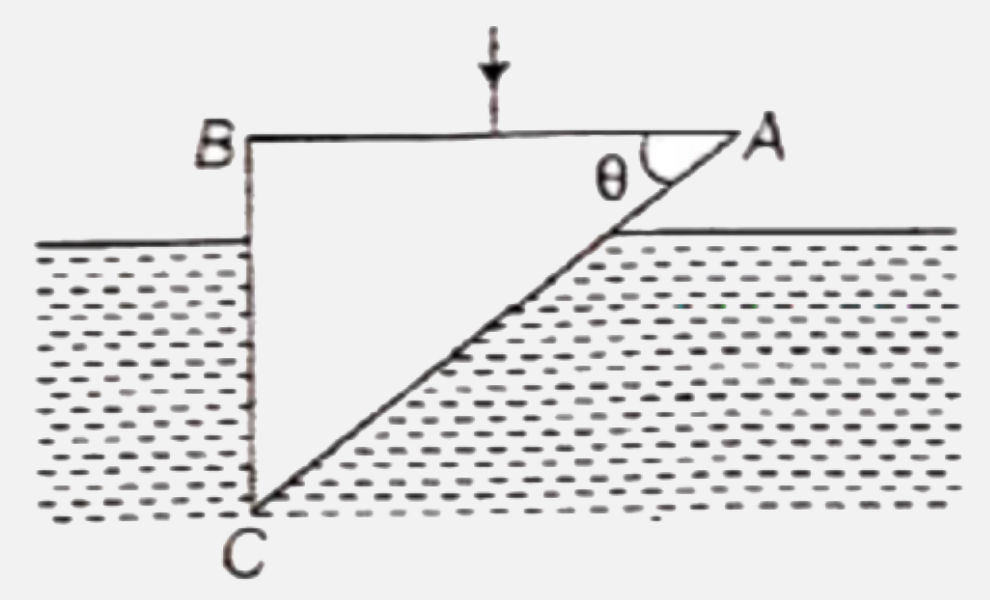
View SolutionA glass prims ABC (refractive index 1.5) , immersed in water (refrective index 43). A ray of light is incident normally one face AB. If it is totally reflected at the face AC, then
View Solution
Knowledge Check
A glass prism of refractive index 1.5 is immersed in water (refractive index 4/3). A light beam incident normally on the face AB is totally reflected to reach on the face BC if
 Asinθ≥89B23<sinθ<89C12<sinθ<89DNone of these
Asinθ≥89B23<sinθ<89C12<sinθ<89DNone of theseA ray of light is incident on the surface of plate of glass of refractive index 1.5 at the polarising angle. The angle of refraction of the ray will be
A33.7∘B23.7∘C43.7∘D53.7∘A glass prism of refractive index 1.5 is immersed in water (refractive index 4/3). A light beam incident normally on the face AB is totally reflected to reach the face BC, Fig. if :
 .AsinC=8/9BsinC=9/8CsinC=2/3DsinC=3/2
.AsinC=8/9BsinC=9/8CsinC=2/3DsinC=3/2
A ray of light is incident on the surface of a glass plate of refractive index 1.6 at polarzing angle. Calculate the angles of reflection and refraction.
View SolutionAn equilateral glass prism of refractive index 1.5 is immersed in water. Find the angle of deviation produced when a ray of light is incident at 42∘ on one face of the prism.
(Refractive index of water = 1.33)
View SolutionA glass prism of refractive index 1.5 is immersed in water (refractive index 4/3). A light beam incident normally on the face AB is totally reflected to reach on the face BC if.

View SolutionFor a given incident ray as shown in Fig., the condition of total internal reflection of ray will be satisfied if the refractive index of the block will be.
 .
.
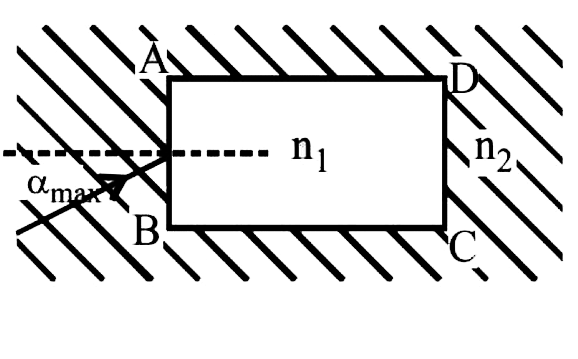
View SolutionA rectengular glass slab ABCD of refractive index n_1 is immersed in water of refractive index n2(n1>n2). A ray of light is incident at the surface AB of the slab as shown. The maximum value of the angle of incidence αmax such that the ray comes out only from the other surface CD is given by
View Solution
