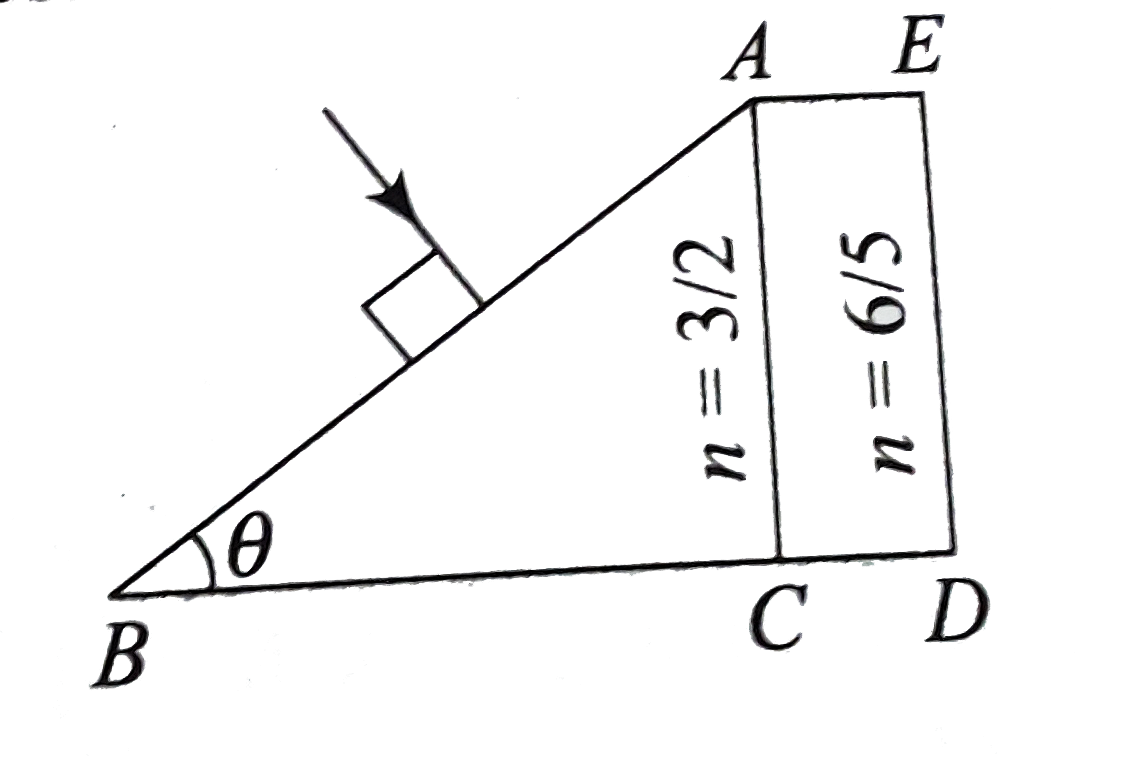
In the figure ABC is the cross-section of a right angled prism and BCDE is the cross-section of a glass slab. The value of theta so that light incident normally on the face AB does not cross the face BC is (Givensin−13/5=37∘)

θ<37∘
θ<53∘
θ≥37∘
θ≥53∘
The correct Answer is:A
sinθC=μRμD=6/53/2=45
r1=0∘⇒r2=<B=90∘−θ
Now, r2>θc
or sinr2>sinθC
∴Sin(90∘−θ)>45
or cosθ>45…(i)
cos37∘=45
From Eq. (i), we see that
θ<37∘
Topper's Solved these Questions
- REFRACTION OF LIGHTBOOK - DC PANDEYCHAPTER - REFRACTION OF LIGHTEXERCISE - Single Correct Option
3 Videos
- REFRACTION OF LIGHTBOOK - DC PANDEYCHAPTER - REFRACTION OF LIGHTEXERCISE - more than one correct option
1 Videos
- REFRACTION OF LIGHTBOOK - DC PANDEYCHAPTER - REFRACTION OF LIGHTEXERCISE - Subjective Questions
8 Videos
- REFLECTION OF LIGHTBOOK - DC PANDEYCHAPTER - REFLECTION OF LIGHTEXERCISE - Subjective
9 Videos
- SEMICONDUCTORSBOOK - DC PANDEYCHAPTER - SEMICONDUCTORSEXERCISE - Subjective
12 Videos
Similar Questions
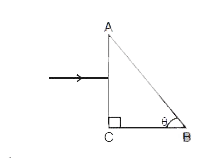
Calculate the value of θ, for which light incident normally on face AB grazes along the face BC.
μglass=3/2andμwater=4/3
View SolutionWhat is the refractive index of the material of the glass prism shown in the figure, if a ray of light incident normally at the face AB emerges along the face AC?
View Solution
Knowledge Check
In figure, ABC is the cross section of a right-angled prism and ACDE is the cross section of a gless slab. The value of θ so that light incident normally on the face AB does not cross the face AC is (given sin−1(3/5)=37∘).
 Aθ≤37∘Bθ<37∘Cθ≤53∘Dθ<53∘
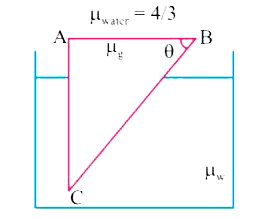
Aθ≤37∘Bθ<37∘Cθ≤53∘Dθ<53∘A glass prism of refractive index 1.5 is immersed in water (refractive index 4/3). A light beam incident normally on the face AB is totally reflected to reach on the face BC if
 Asinθ≥89B23<sinθ<89C12<sinθ<89DNone of these
Asinθ≥89B23<sinθ<89C12<sinθ<89DNone of theseA glass prism of refractive index 1.5 is immersed in water (refractive index 4/3). A light beam incident normally on the face AB is totally reflected to reach on the face BC if.
 Asinθ≥89B23<sinθ<89Csinθ≤23DNone of these
Asinθ≥89B23<sinθ<89Csinθ≤23DNone of these
What should be the value of angle θ so that light entering normally through the surface AC of a prism (n=3/2) does not cross the second refracting surface AB?

View SolutionWhat should be the value of angle so that light entering normally through the surface AC of a prism (n = 3/2) does not cross the second refracting surface AB.
View SolutionFigure shows a right angled prism ABC having refractive μg=32 lowered into water (μω43). Find angle α so that the incident ray normal to face AB will be reflected at face BC completely.
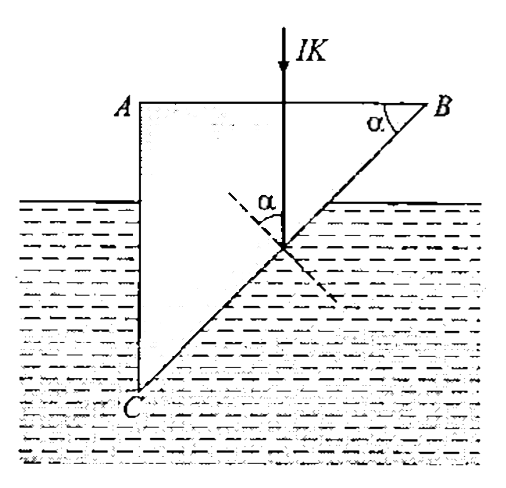
View SolutionA glass prism of refractive index 1.5 is immersed in water (refractive index 4/3). A light beam incident normally on the face AB is totally reflected to reach the face BC, Fig. if :
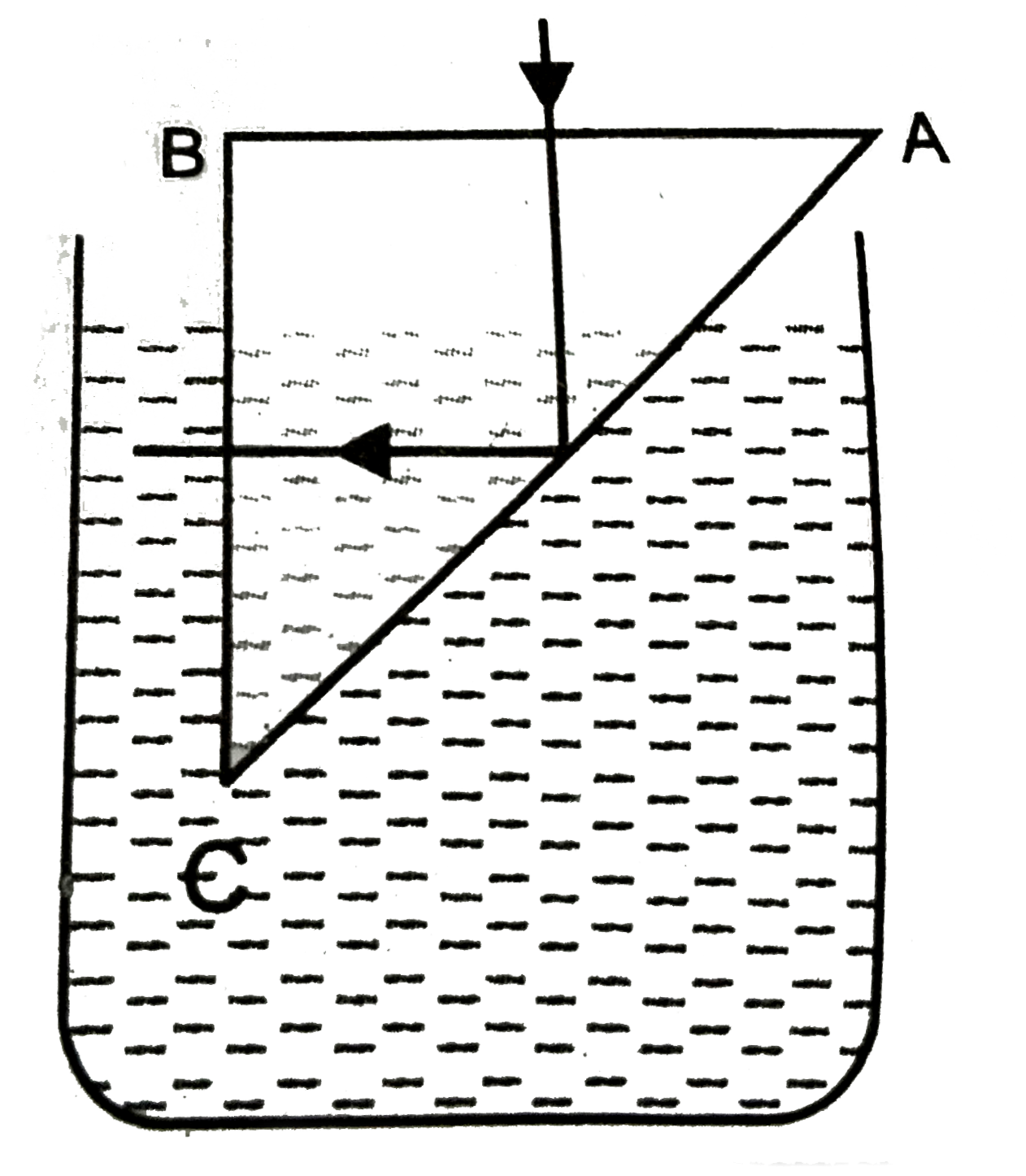 .
.
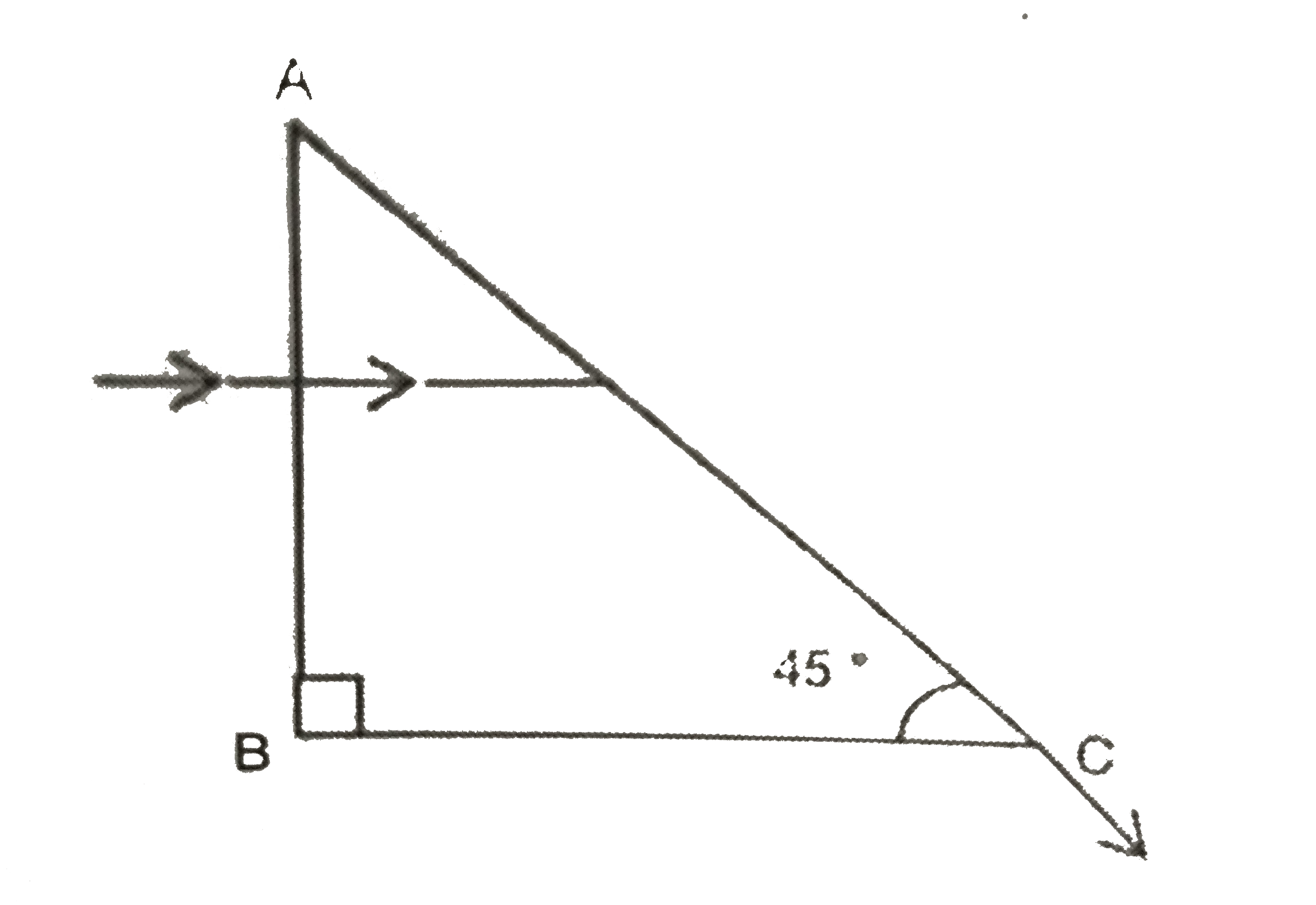
View SolutionAn equilateral triangular prism is made of glass (μ=1.5). A ray of light is incident normally on one of the faces. The angle between the incident and emergent ray is
View Solution
