A current of 50A is placed through a straight wire of length 6cm then the magnetic induction at a point 5cm from the either end of the wire is (1gauss=10−4T)
2.5gauss
1.25gauss
1.5gauss
3.0gauss
The correct Answer is:C
To find the magnetic induction (magnetic field) at a point 5 cm from either end of a straight wire carrying a current of 50 A, we can use the formula for the magnetic field around a long straight conductor.
1. Identify the Parameters:
- Current (I) = 50 A
- Length of the wire (L) = 6 cm = 0.06 m
- Distance from the wire (r) = 5 cm = 0.05 m
2. Determine the Angles:
- The point where we want to find the magnetic field is 5 cm from either end of the 6 cm wire. This means that the distance from the center of the wire to the point is:
d=√(3 cm)2+(5 cm)2=√(0.03 m)2+(0.05 m)2=√0.0009+0.0025=√0.0034≈0.0583 m
- The angles (α and β) from the wire to the point can be calculated using trigonometry. Since the point is symmetric with respect to the wire, both angles are equal.
3. Use the Formula for Magnetic Field:
- The magnetic field (B) at a distance r from a long straight conductor is given by:
B=μ0I4πr⋅(sinα+sinβ)
- Since α = β, we can write:
B=μ0I4πr⋅2sinα
4. Calculate the Sine Values:
- For α (which is the angle opposite to the distance r), we can use:
sinα=5 cmd=0.050.0583≈0.858
- Thus, sinα+sinβ=2⋅0.858≈1.716.
5. Substitute Values into the Formula:
- The permeability of free space (μ₀) = 4π×10−7 T m/A.
- Now substituting the values:
B=(4π×10−7)⋅504π⋅0.05⋅1.716
- Simplifying:
B=(10−7)⋅500.05⋅1.716=5×10−60.05⋅1.716=1.5×10−4 T
6. Convert to Gauss:
- Since 1 Gauss=10−4 T:
B=1.5 Gauss
Final Answer:
The magnetic induction at a point 5 cm from either end of the wire is 1.5 Gauss.
- Current (I) = 50 A
- Length of the wire (L) = 6 cm = 0.06 m
- Distance from the wire (r) = 5 cm = 0.05 m
- The point where we want to find the magnetic field is 5 cm from either end of the 6 cm wire. This means that the distance from the center of the wire to the point is:
d=√(3 cm)2+(5 cm)2=√(0.03 m)2+(0.05 m)2=√0.0009+0.0025=√0.0034≈0.0583 m
- The angles (α and β) from the wire to the point can be calculated using trigonometry. Since the point is symmetric with respect to the wire, both angles are equal.
- The magnetic field (B) at a distance r from a long straight conductor is given by:
B=μ0I4πr⋅(sinα+sinβ)
- Since α = β, we can write:
B=μ0I4πr⋅2sinα
- For α (which is the angle opposite to the distance r), we can use:
sinα=5 cmd=0.050.0583≈0.858
- Thus, sinα+sinβ=2⋅0.858≈1.716.
- The permeability of free space (μ₀) = 4π×10−7 T m/A.
- Now substituting the values:
B=(4π×10−7)⋅504π⋅0.05⋅1.716
- Simplifying:
B=(10−7)⋅500.05⋅1.716=5×10−60.05⋅1.716=1.5×10−4 T
- Since 1 Gauss=10−4 T:
B=1.5 Gauss
The magnetic induction at a point 5 cm from either end of the wire is 1.5 Gauss.
Topper's Solved these Questions
- MAGNETICSBOOK - DC PANDEYCHAPTER - MAGNETICSEXERCISE - INTRODUCTORY EXERCISE
1 Videos
- MAGNETICSBOOK - DC PANDEYCHAPTER - MAGNETICSEXERCISE - SUBJECTIVE_TYPE
1 Videos
- MAGNETICSBOOK - DC PANDEYCHAPTER - MAGNETICSEXERCISE - MCQ_TYPE
1 Videos
- MAGNETIC FIELD AND FORCESBOOK - DC PANDEYCHAPTER - MAGNETIC FIELD AND FORCESEXERCISE - Medical entrance s gallery
59 Videos
- MAGNETISM AND MATTERBOOK - DC PANDEYCHAPTER - MAGNETISM AND MATTEREXERCISE - Medical gallery
1 Videos
Similar Questions
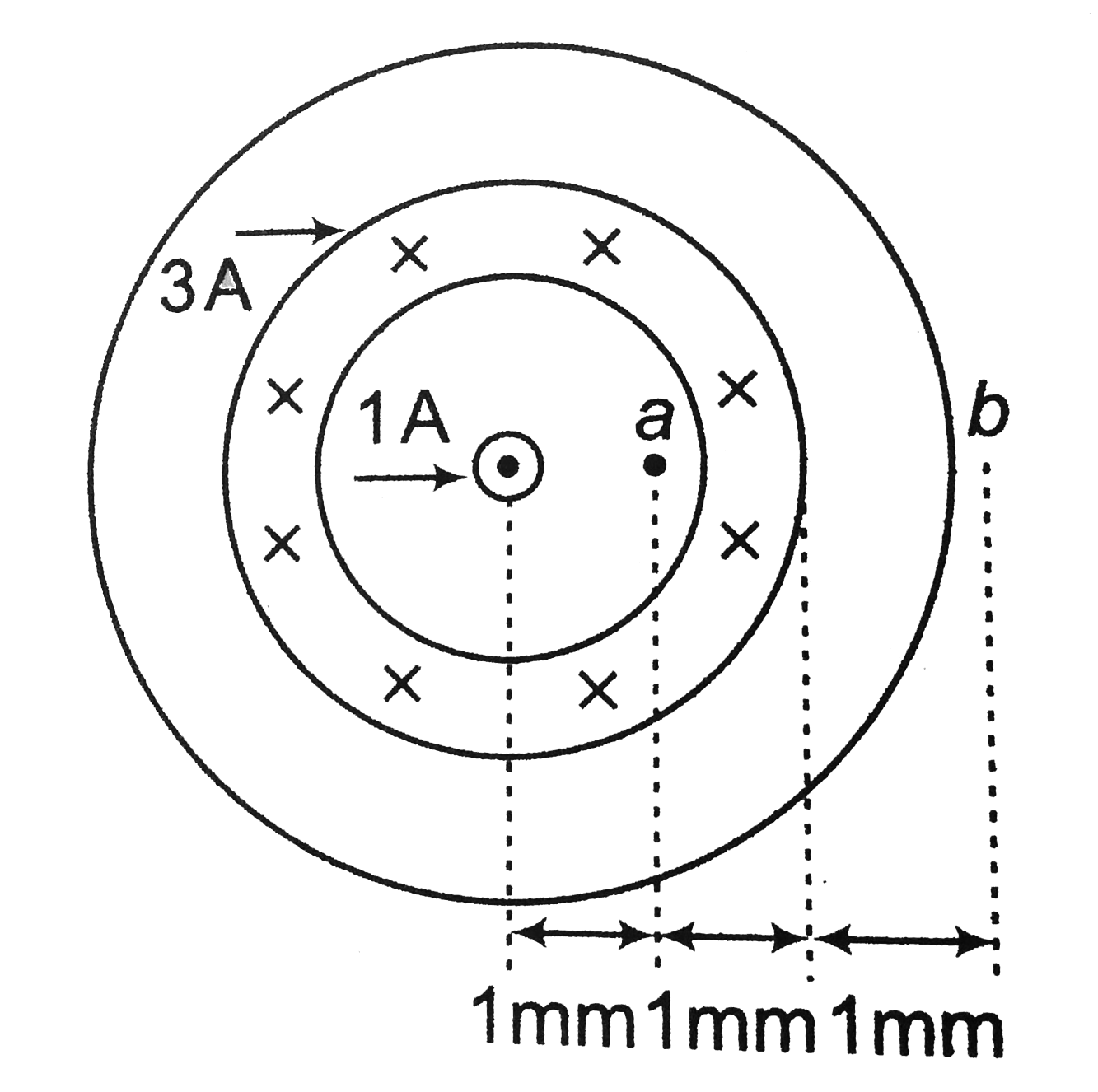
Figure given in the question is a cross-sectional view of a coaxial cable. The centre conductor. surrounded by a rubber layer, which is surrounded by an outer conductor, which is surround by another rubber layer. The current in the inner conductor is 1.0A out of the page, and the current in the outer conductor is 3.0 A into the page. Determine the magnitude and direction of the magnetic field at points a and b.
View SolutionIn the Bohr model of the hydrogen atom, in the lowest energy state the electron revolves round the proton at a speed of 2.2×106ms in a circular orbit of radius 5.3×10−11 m.
(a) What is the orbital period of the electron?
(b) If the orbiting electron is considered to be a current loop, what is the current I? (c) What is the magnetic moment of the atom due to the motion of the electron?
View SolutionTwo circular coil of radii 5cm and 10cm carry equal currents of 2A. The coils have 50 and 100 turns, respectively, and are placed in such a way that their planes as well as their centers coincide. Magnitude of magnetic field at the common centre of coils is
View SolutionA long wire carries a steady curent . It is bent into a circle of one turn and the magnetic field at the centre of the coil is B. It is then bent into a circular loop of n turns. The magnetic field at the centre of the coil will be
View SolutionA bar magnet is hung by a thin cotton thread in a uniform horizontal magnetic field and is in equilibrium state. The energy required to rotate it by 60∘ is W. Now the torque required to keep the magnet in this new position is
View SolutionA current of 5 flowing is passed through a straight wire of length 6cm, then the magnetic induction at a point 5cm from the either end of the wire is :
View SolutionA long straight wire carrying a current of 25A is placed in an external uniform magnetic field 3⋅0×10−4T parallel to the current. Find the magnitude of the resultant magnetic field at a point 1⋅5cm away from the wire.
View SolutionA current of 1A is flowing through a straight conductor of length 16cm. The magnetic induction ( in tesla ) at a point 10cm from the either end the wire is :
View SolutionThe magnetic induction at any point due to a long straight wire carrying a current is
View Solutionकिसी लंबे, सीधे धारावाही तार से प्रवाहित विधुत-धारा होगी, यदि तार से 10 cm की दूरी पर उत्पन्न चुंबकीय क्षेत्र 2 mTहो ?
View SolutionThe magnetic induction at 0.1 m from a very long straight wire carrying a current of 5A is 10^(-6) Wb//m^(2) . What will be the magnetic induction at 0.2 m from the wire if the current through it is increased to 20 A?
View SolutionA current of 1 ampere is passed through a straight wire of length 2.0 meters. What value of magnetic field at a point in air at a distance of 3 meters from either end of wire and on the axis of wire ?
View SolutionMagnetic field at 10 cm from extremely long current carrying straight wire is 10^(-5)Wb//m^(2) . Then current passing through this wire is ______ .
View SolutionA long straight wire carries a current of 50 A. What is the magnitude of intensity of magnetic induction at a point 15 cm from the wire.
View SolutionA current of 50 A is placed through a straight wire of length 6 cm then the magnetic induction at a point 5cm from the either end of the wire is ( 1gauss=10^-4T )
View Solution
