Twelve identical resistances arranged on all edges of a cube. The resistors are all the same. Then find the equivalent resistance between the edges A and B as shown in figure.

a. Between 1 and 4: Points 2 and 5 are symmetrically located w.r.t points 1 and 4. so, they are at same potentials
similarly points 3 and 8 also symmetircally located w.r.t point 1 and 4. So they are again at same potential. Now, we have 12 resistors each of resistance r connected across 1 and 2, 2 and 3,...., etc. So redrawing them wiht the assumption that 2 and 5 are at same ptential and 3 and 8 are at same potential. The new figure is a shown in figure.
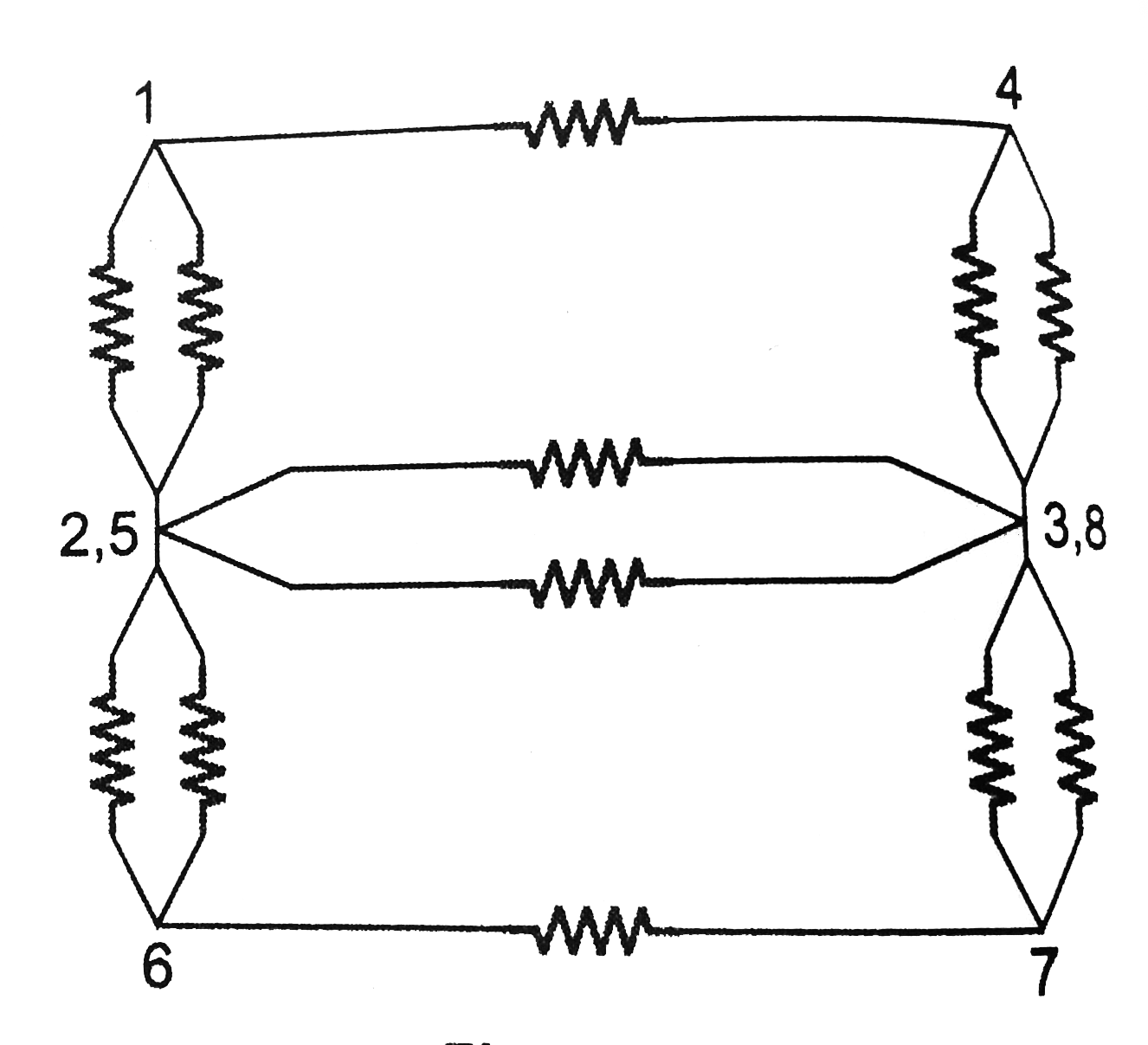
Now we had to find the equivalent resistance between ltbr> 1 and 4. We can now simplify the circuit as
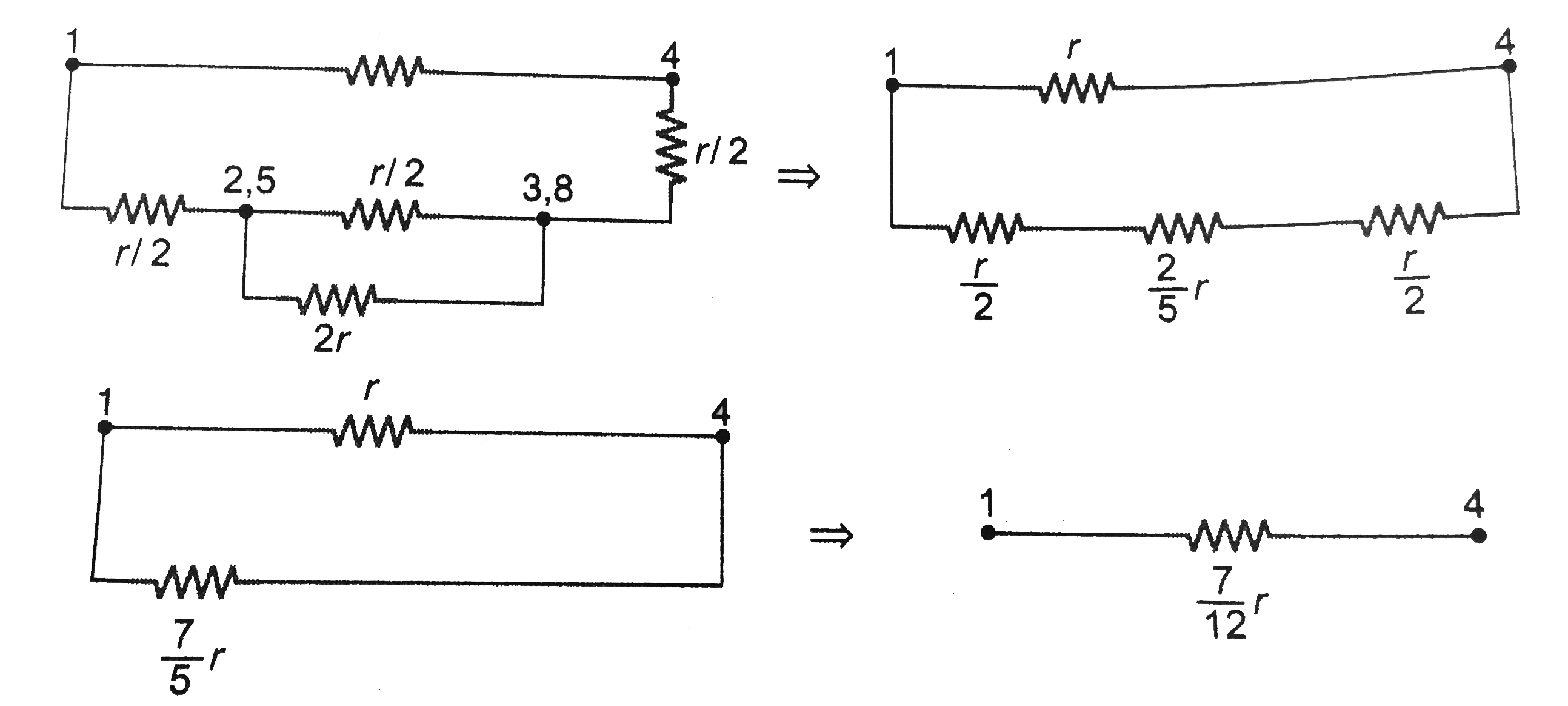
Thus, the equivalent resistance between points 1 and 4 is 712r.
b. Between 1 and 3: Points 6 and 8 are symmetrically located w.r.t points 1 and 3. Similarly points 2 and 4 are located symmetrically w.r.t points 1 and 3. So, points 6 and 8 are at the same potential. similarly 2 and 4 are at same potentials. Redrawing the simple circuit we have figure. 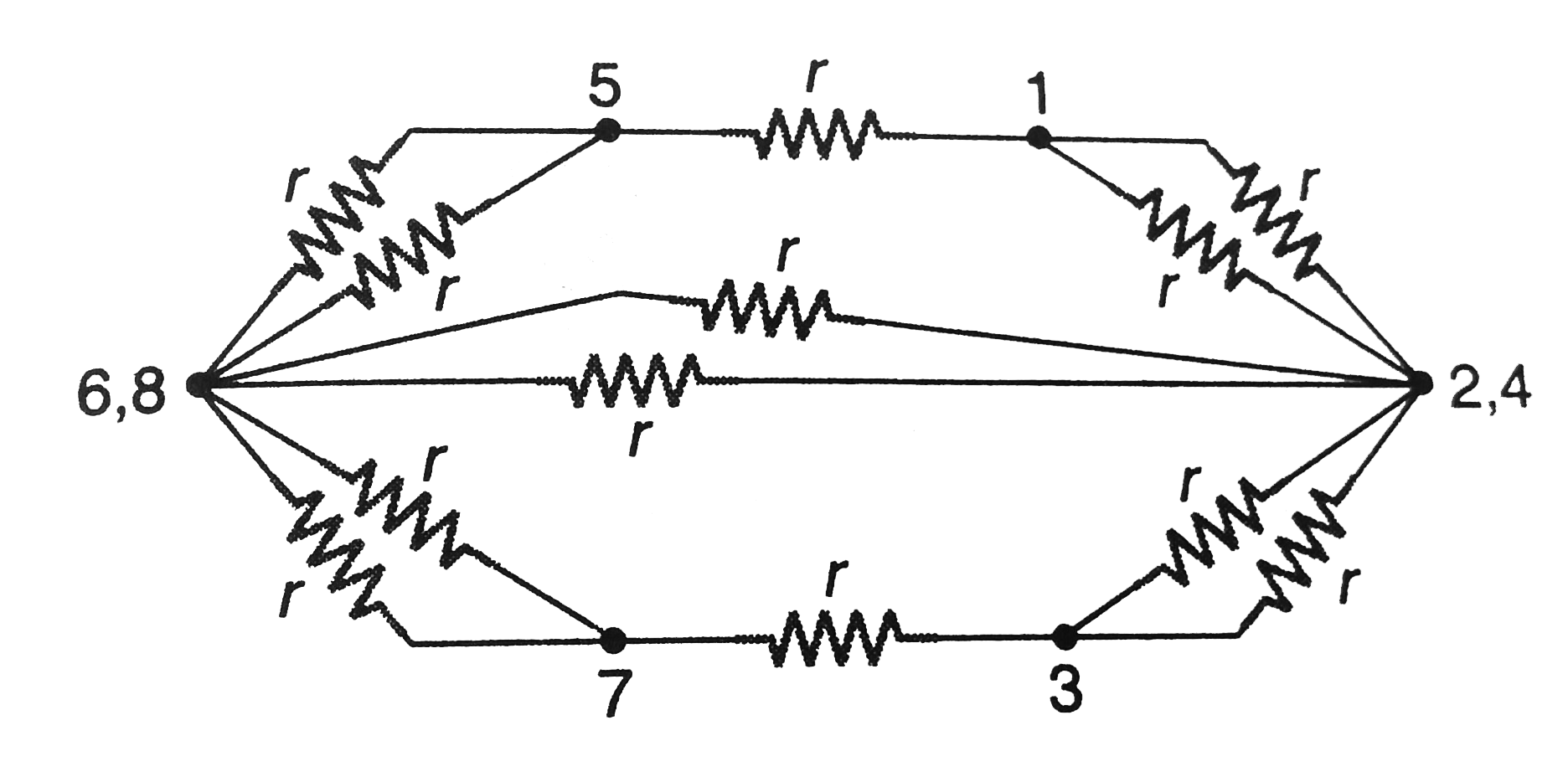
Between 1 and 3, a balanced Wheatstone bridge is formed as shown in figure. So, the resistance betwen 2 and 6 and between 4 and 8 can be removed.
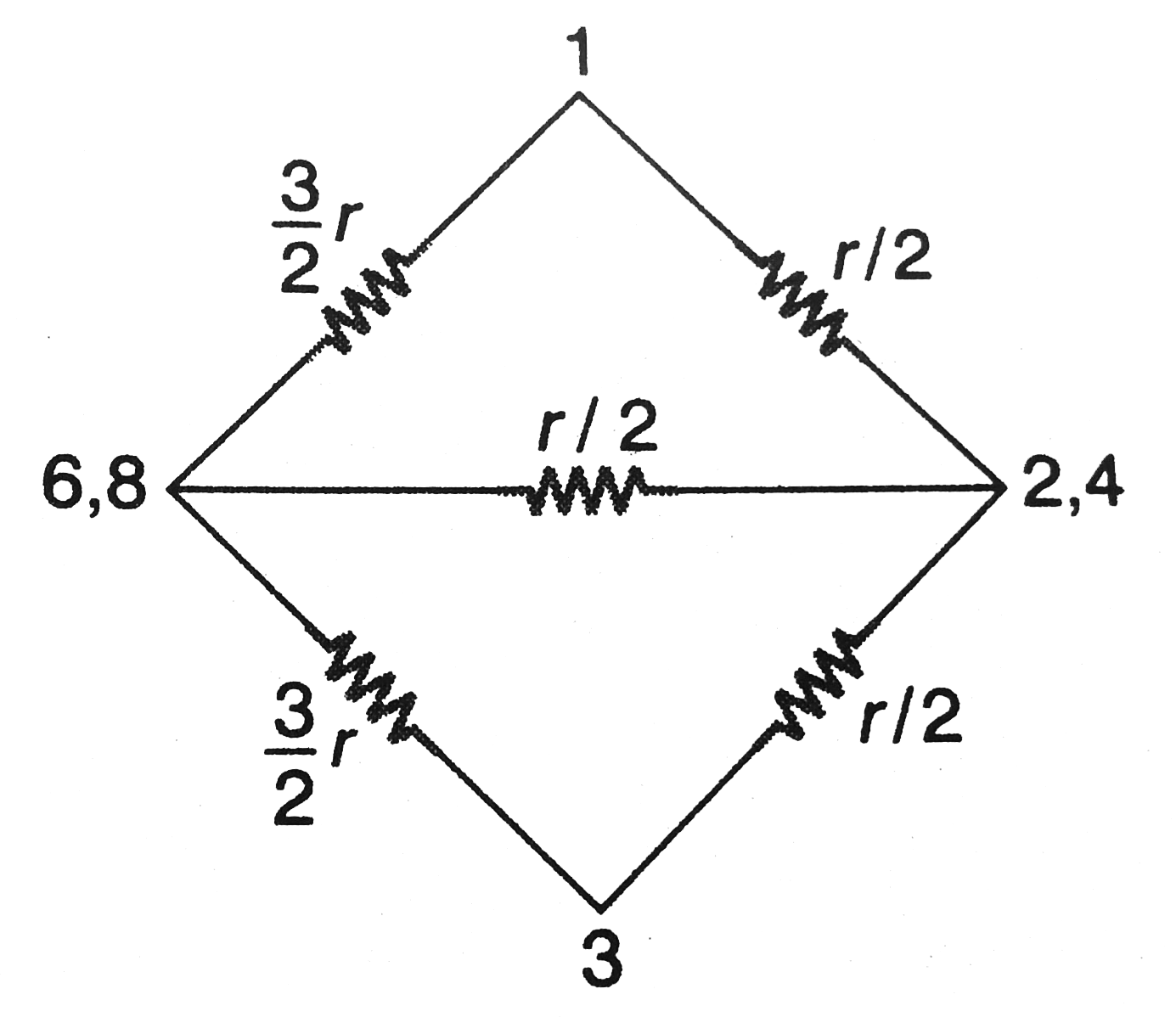
Thus, the equivalent resistance between 1 and 3 is 34r
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - CAPACITORSEXERCISE - Exercise155videos
CAPACITORS
- BOOK - DC PANDEYCHAPTER - CAPACITORSEXERCISE - OBJECTIVE_TYPE1videos
CAPACITORS
- BOOK - DC PANDEYCHAPTER - ATOMSEXERCISE - MEDICAL ENTRANCES GALLERY42videos
ATOMS
- BOOK - DC PANDEYCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective11videos
COMMUNICATION SYSTEM
Similar Questions
Twelve identical resistances arranged on all edges of a cube. The resistors are all the same. Then find the equivalent resistance between the edges A and B as shown in.
 View Solution
View SolutionTweleve indentical resistor are arranged on all edfges of a cube. Then find the equivalent resistance between the corners 1 and 6 as shwon in fig 5.126(us nodal method)
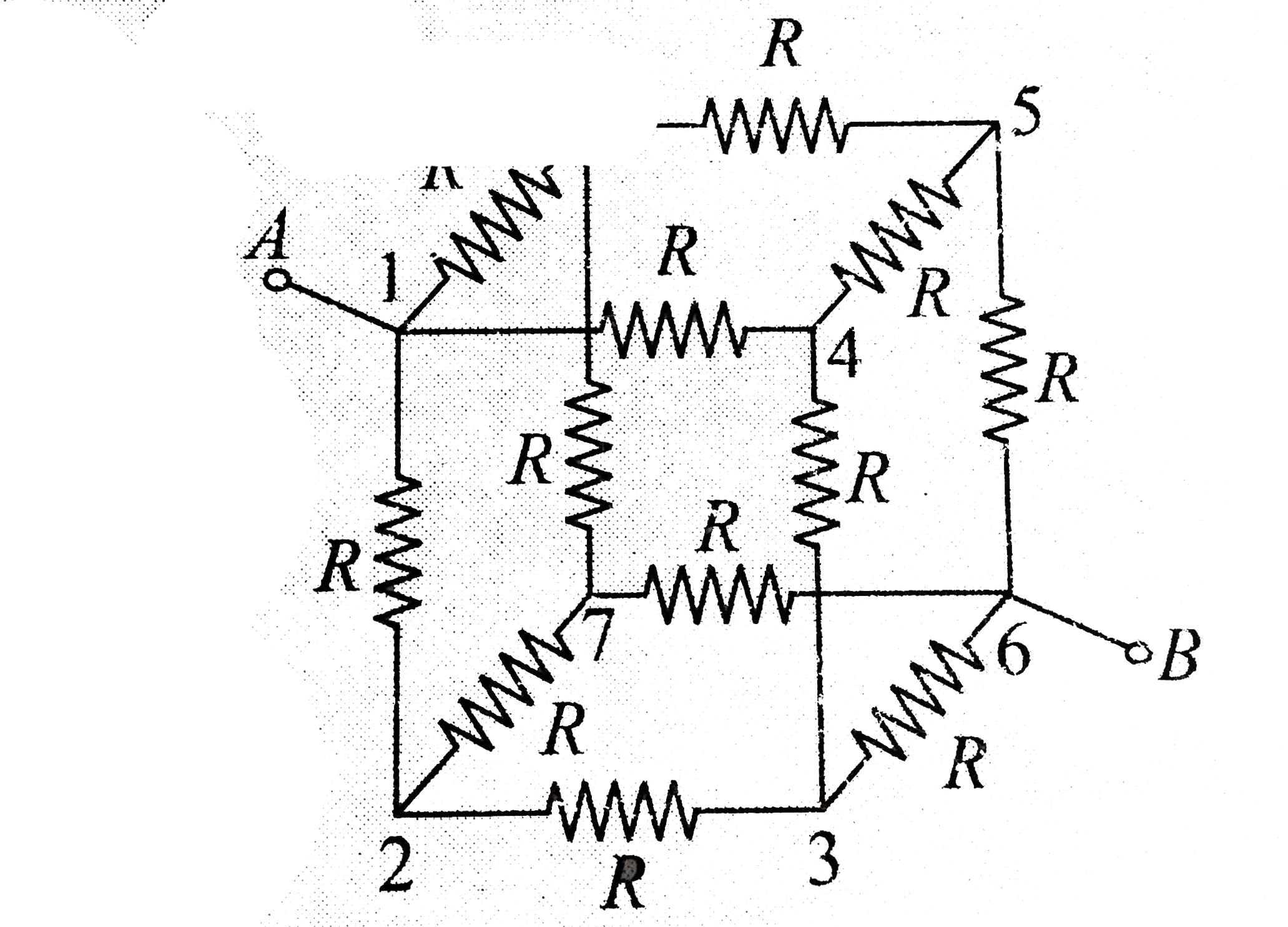 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
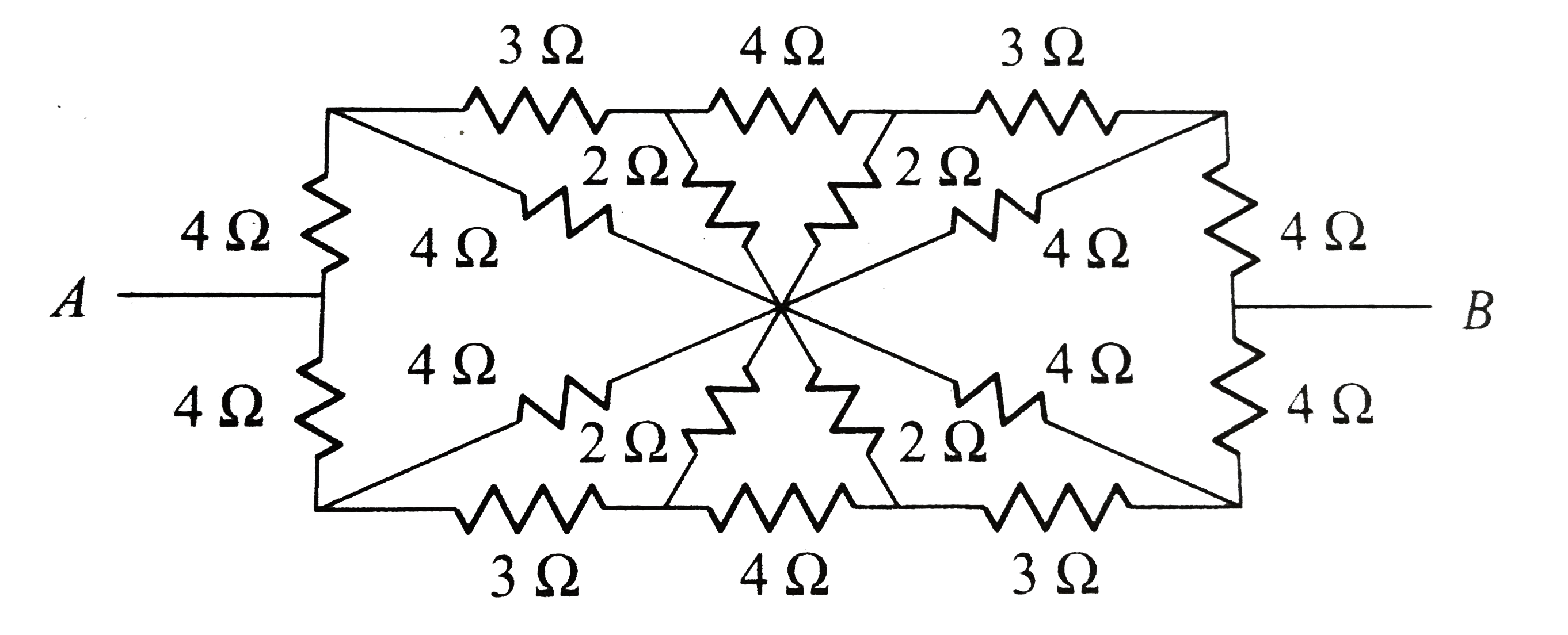
The equivalent resistance between A and B for the mesh shown in the figure is
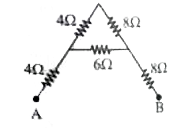 A16ΩB30ΩC4.8ΩD7.2Ω
A16ΩB30ΩC4.8ΩD7.2Ω - Question 2 - Select One
Find the equivalent resistance between A and B in the given figure.
 A18ΩB2ΩC9ΩD6Ω
A18ΩB2ΩC9ΩD6Ω - Question 3 - Select One
Find the equivalent resistance between the point a and b of the network shown in figure.
 A3B2C1D5
A3B2C1D5
Find the equivalent resistance between the point a and b of the circuit shown in figure
View SolutionFind the equivalent resistance between point a and b in the network shown in figure.
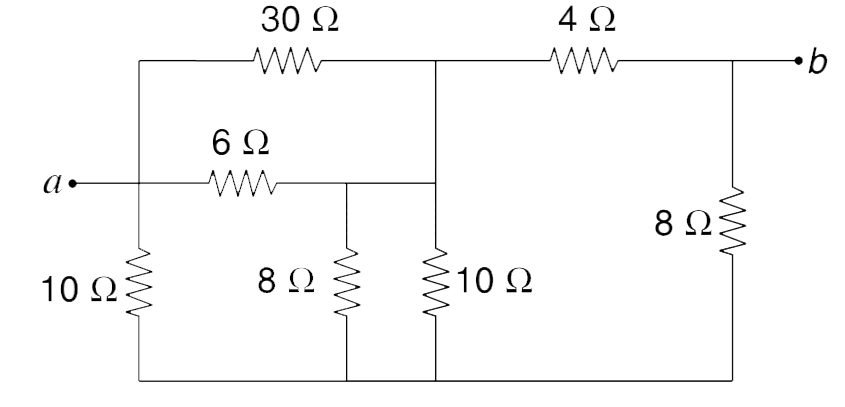 View Solution
View SolutionFind the equivalent resistance between A and B in the give figure .
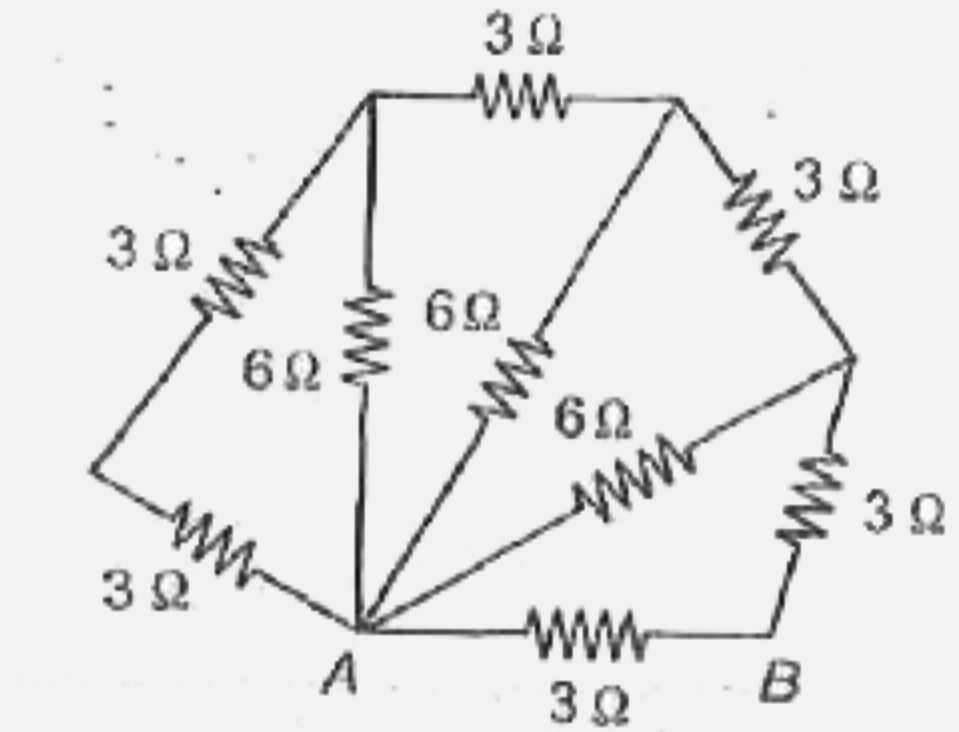 View Solution
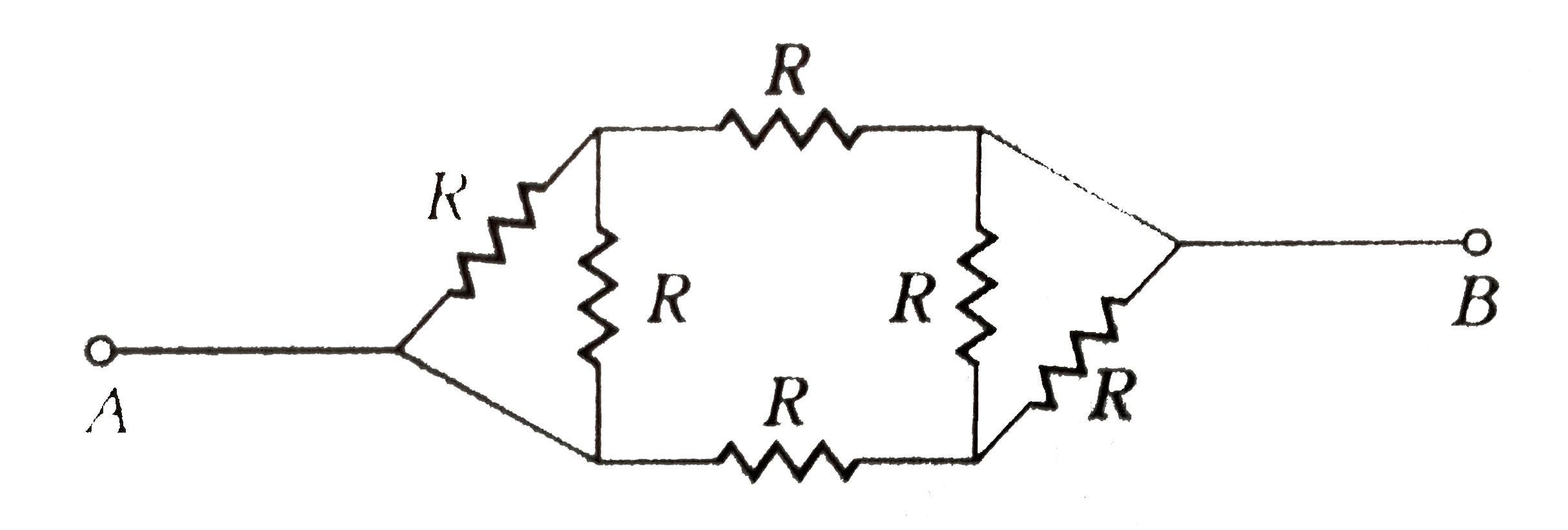
View SolutionA number of resistors are connected as shown in the figure. The equivalent resistance between A and B is
 View Solution
View SolutionThe equivalent resistance resistance between A and B of network shown in figure is
 View Solution
View Solution

