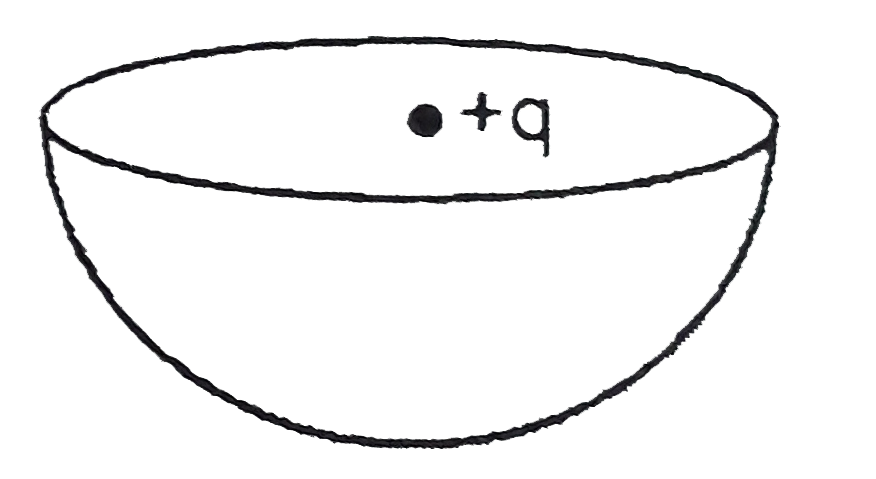
A point charge q is placed at the origin. Calculate the electric flux

A charge 2q is placed at the mouth of a conical flask. The electric flux through the flask will be
Azero
B $\frac{Q}{ε_{0}}$
C $\frac{Q}{2 ε_{0}}$
D $< \frac{Q}{2 ε_{0}}$
Charge of 2 C is placed at the centre of a cube. What is the electric flux passing through one face ?
A $\frac{1}{(3 ε_{0})}$
B $(\frac{1}{4}) ε_{0}$
C $\frac{2}{ε_{0}}$
D $\frac{3}{ε_{0}}$
A point charge Q is placed at one of the vertices of a cubical block. The electric flux flowing through this cube is
A $\frac{Q}{6 ε_{0}}$
B $\frac{Q}{4 ε_{0}}$
C $\frac{Q}{8 ε_{0}}$
D $\frac{Q}{ε_{0}}$

A point charge q is placed at the origin. Calculate the electric flux through the open hemispherical surface ${(x - a)}^{2} + y^{2} + z^{2} = a^{2}, x \geq a$