The axle of a pulley of mass 1kg is attached to the end of an elastic string of length 1m, cross- sectional area 10−3m2 and young's modulus 2×105Nm−2,whose other end is fixed to the ceiling. A rope of negligible mass is placed on the pulley such that its left end is fixed to the ground and its right end is hanging freely , from the pulley which is at rest in equilibrium . Now, the rope and the pulley can be neglected. (Given, g=10ms−2)

The elongation of the string before applying force is
35cm
30cm
0.5cm
0.05cm
The correct Answer is:C
Force constant of string is
k=ForceElongation
=FFL/Y
or k=YAL=1×105×10−31
=200Nm−1
Initial elastic potential energy of string
=12k(0.05)2
12(200)(25×10−4)
=25×10−2J
Let after force F=10N is applied extra enlongation is x, then
0.25+30x=12(200)(x2+25×10−4+0.1x)
0.25+30x=100x2+0.25+10x
∴100x2=20x
rArr x=20100=15m=0.2m
=20cm
xmax=20+5=25cm
Topper's Solved these Questions
- ELASTICITYBOOK - DC PANDEYCHAPTER - ELASTICITYEXERCISE - Level 2 Subjective
10 Videos
- ELASTICITYBOOK - DC PANDEYCHAPTER - ELASTICITYEXERCISE - Example
39 Videos
- ELASTICITYBOOK - DC PANDEYCHAPTER - ELASTICITYEXERCISE - Level 2 More Than One Correct
8 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEYCHAPTER - CURRENT ELECTRICITYEXERCISE - All Questions
434 Videos
- ELECTROSTATICSBOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - Integer
17 Videos
Similar Questions
A pulley fixed to the ceiling carried a thread with bodies of masses m1 and m2 attached to its ends. The mases of the pulley and the thread are negligible and friction is absent. Find the acceleration of the centre of mass of this system.
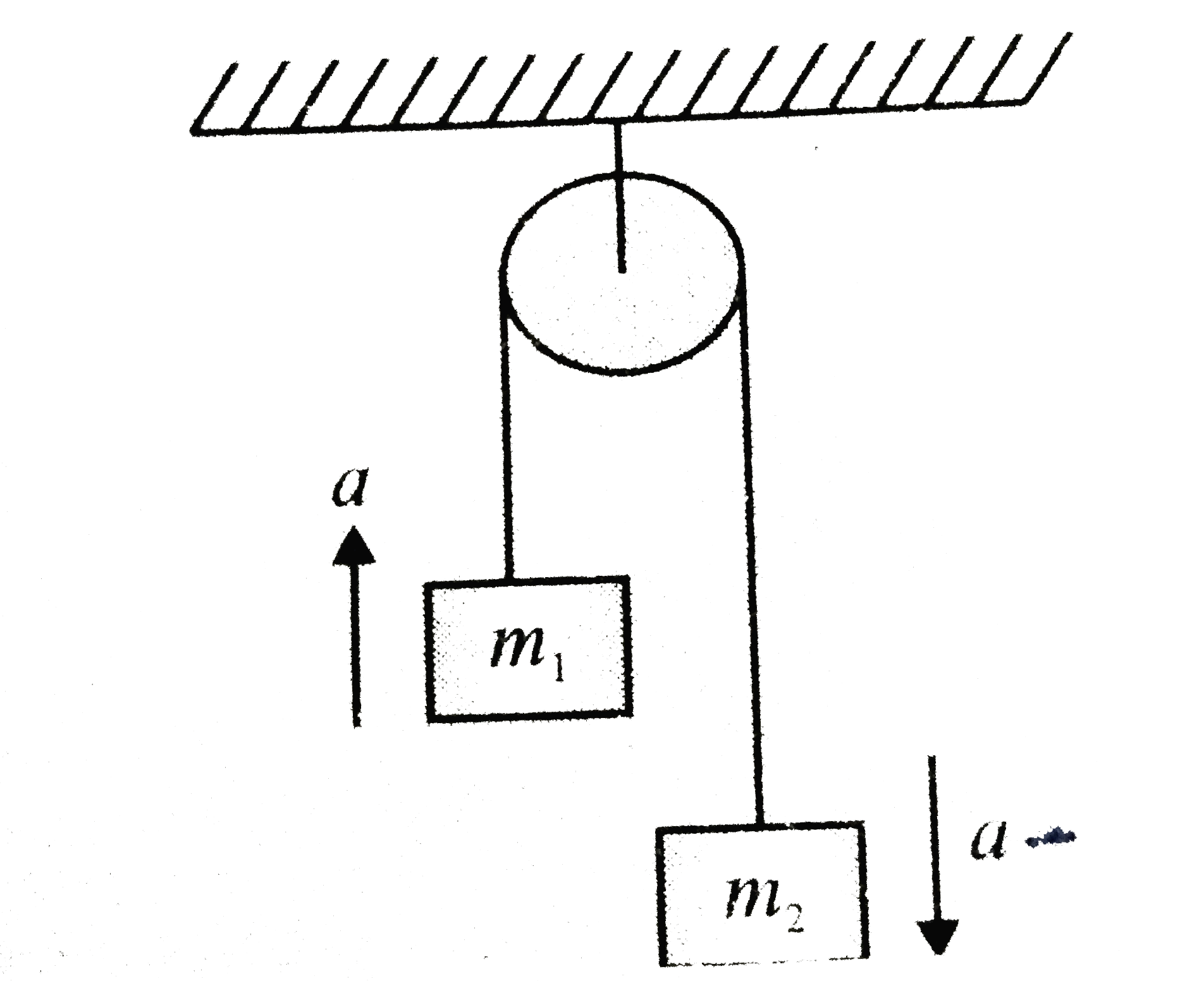
View SolutionA pulley fixed to the ceiling carries a thread with bodies of masses m1 and m2 attached to its ends. The masses of the pulley and the thread are negligible, friction is absent. Find the acceleration wC of the centre of inertia of this system.
View Solution
Knowledge Check
A body of mass M is attached to the lower end of a metal wire, whose upper end is fixed . The elongation of the wire is l.
ALoss in gravitational potential energy ofM is MglBThe elastic potential energy stored in the wire is MglCThe elastic potential energy stored in the wire is 12MglDHeat produced is 12MglA wire of length 1 m and its area of cross-section is 1 cm2 and Young's modulus of the wire is 1011N/m2. Two forces each equal to F are applied on its two ends in the opposite directions. If the changein length is 1 mm, then the value of F will be
A0.5×104NB104NC2×104ND108NAn iron rod of length 2m and cross section area of 50mm2, stretched by 0.5 mm, when a mass 250 kg is hung from its lower end. Young's modulus of the iron rod is
A19.6×1010N/m2B19.6×1015N/m2C19.6×1018N/m2D19.6×1020N/m2
A string of length L is fixed at one end and carries a mass M at the other end. The string makes 2π rev/s around the vertical axis through the fixed end as shown in figure, then tension in string is
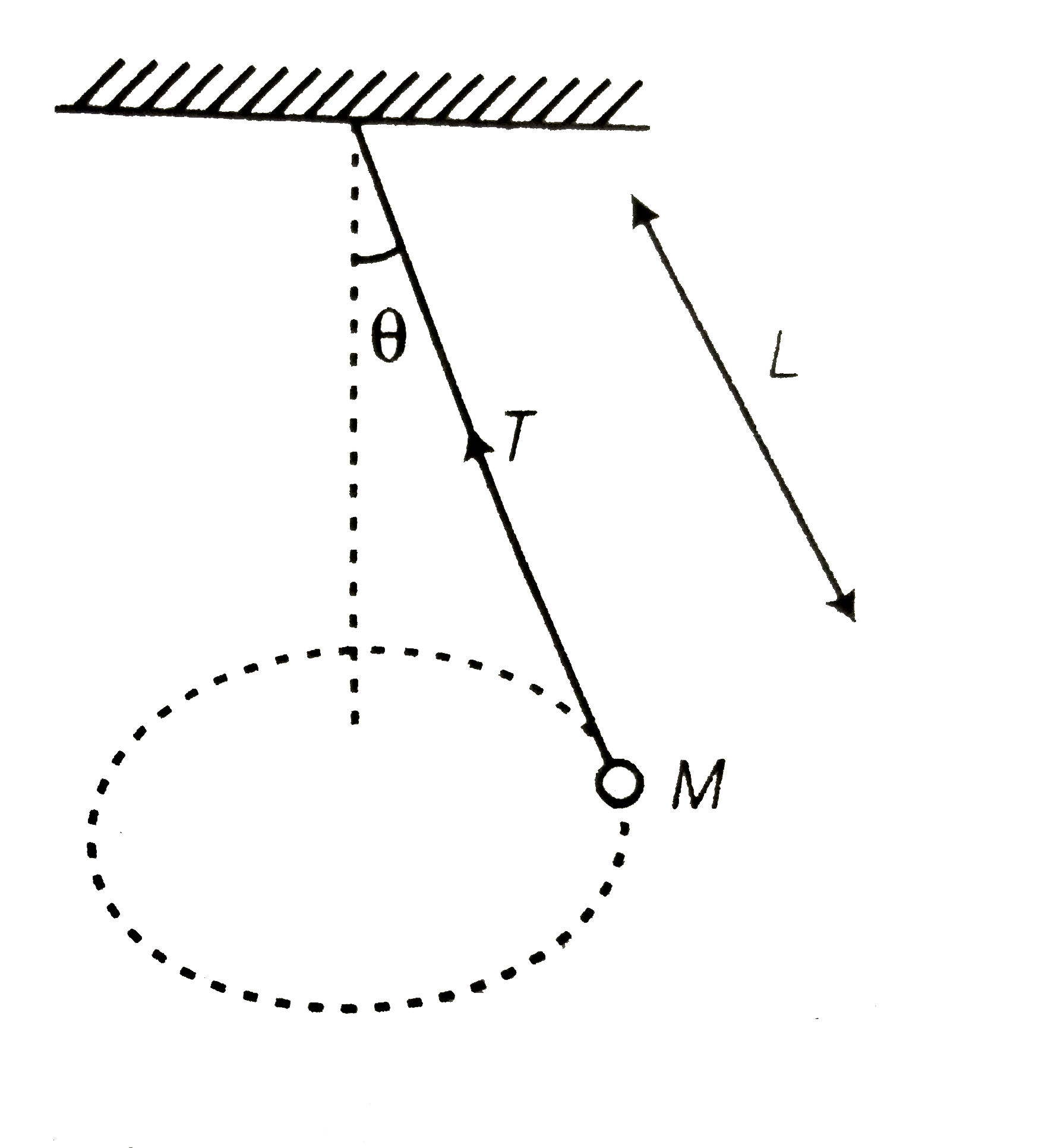
View SolutionA string of negligible mass is wrapped on a cylindrical pulley of mass M and radius R. The other end of string is tied to a bucket of mass m. If the pulley rotates about a horizontal axis then the tension in the string is :
View SolutionA metal wire of negligible mass, length 1 m and cross-sectional area 10−6m2 is kept on a smooth horizontal table with one end fixed on the table. A ball of mass 2kg is attached to the other end of the wire. When the wire and the ball are rotated with angular velocity of 20 rad/s, it is found that the wire is elongated by 10−3m. If the Young's modulus of the metal is n×1011N/m2, then the value of n is
View SolutionA block of mass 2m is hanging at the lower and of a ropeof mass m and length the l, the other end being fixed to the ceililng. A pulse of wavelength λ0 is produced at the lower of the rope.
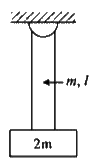
The speed of the pulseat the mid point of rope is:
View SolutionIf two wires of same length l and are of the cross-section A with young modulus Y and 2Y connect in series and one end is fixed on roof and another end with mass m makes simple harmonic motion, then the time period is
View Solution