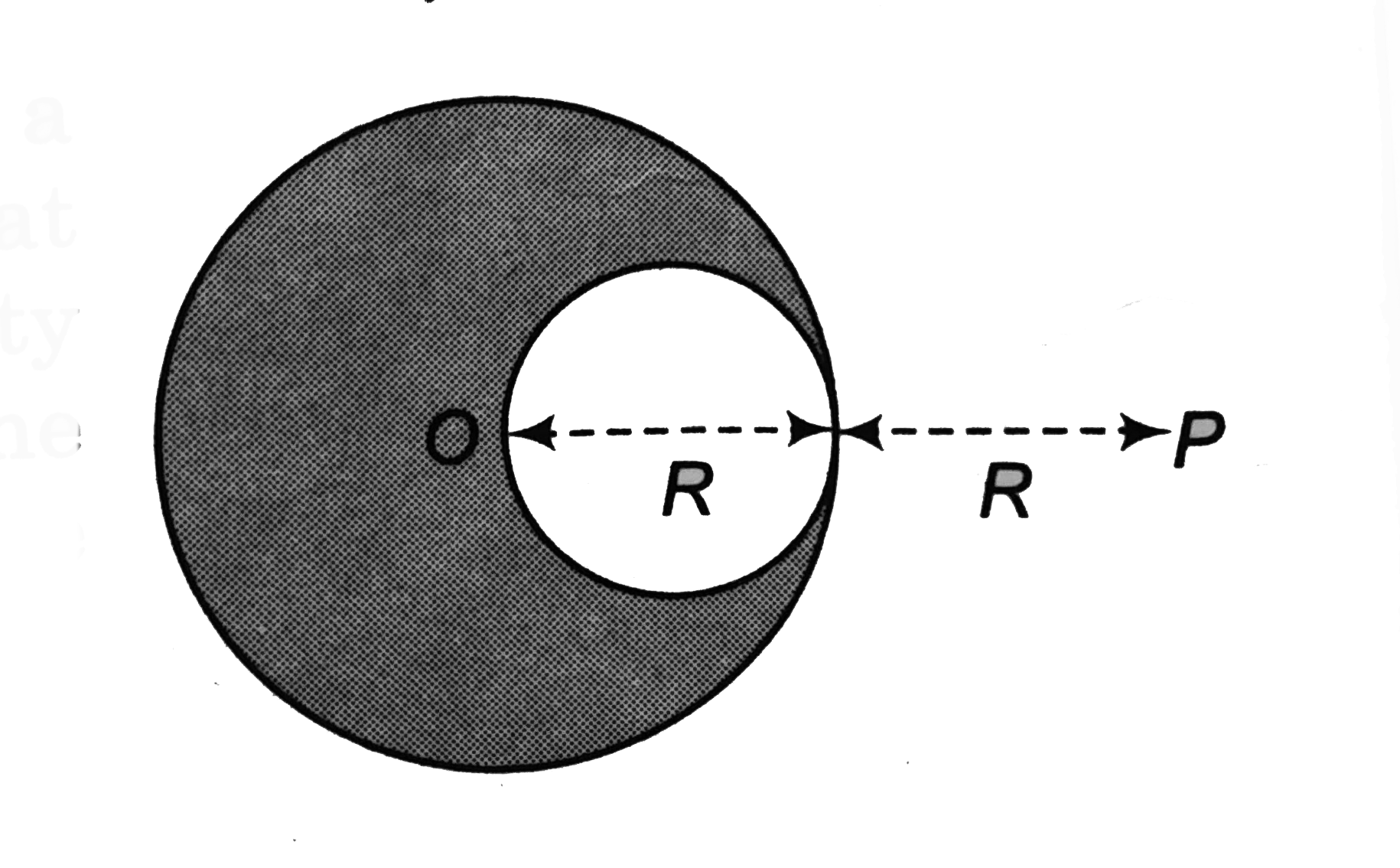
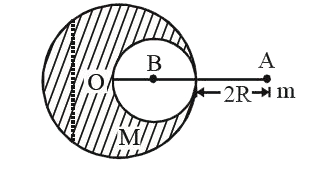
A solid sphere of uniform density and radius R applies a gravitational force attraction equal to F1 on a particle placed at P, distance 2R from the centre O of the sphere. A spherical cavity of radius R/2 is now made in the sphere as shows in figure. The particle with cavity now applies a gravitational force F2 on same particle placed at P. The radio F2/F1 will be
1/2
7/9
3
7
The correct Answer is:B
C→cavity, T→ Total, R→ remaining
F1=GMm(2R)2..(i)
FR=F2=FT−FC=F1−FC
or F2=GMm(2R)2−G(M8)m(3R/2)2
or F2=14GMm72R2
From Eqs. (i) and (ii) we get,
F2F1=79
Topper's Solved these Questions
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - Level 2 More Than One Correct
10 Videos
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - Level 2 Subjective
14 Videos
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - Level 1 Subjective
19 Videos
- GENERAL PHYSICSBOOK - DC PANDEYCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
- KINEMATICSBOOK - DC PANDEYCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
11 Videos
Similar Questions
A solid sphere of uniform density and radius R applies a gravitational force of attraction equal to F1 on a particle placed at a distance 3R from the center of the sphere. The 1 sphere with the cavity now applies a gravitational force F2, on the same particle. Then ratio F1F2 is
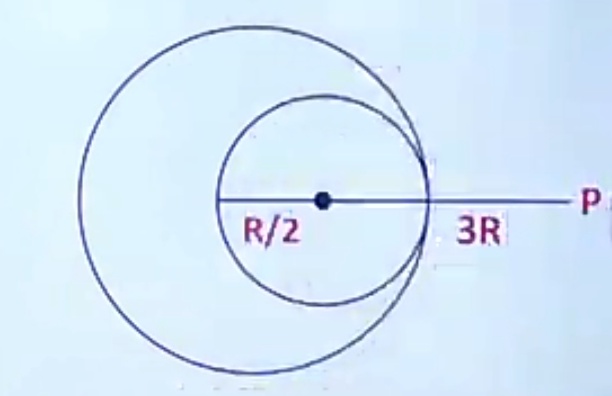
View SolutionThe gravitational force acting on a particle, due to a solid sphere of uniform density and radius R, at a distance of 3R from the centre of the sphere is F1. A spherical hole of radius (R/2) is now made in the sphere as shown in diagram. The sphere with hole now exerts a force F2 on the same particle. ratio of F1 to F2 is
View Solution
Knowledge Check
A solid sphere of uniform density and radius R applies a gravitational force of attraction equal to F1 on a particle placed at P, distance 2R from the centre O of the sphere. A spherical cavity of radius R/2 is now made in the sphere as shown in given figure. The sphere with cavity now applies a gravitational force F2 on same particle placed at P. The ratio F2/F1 will be
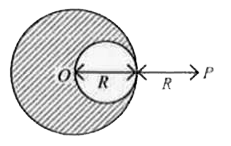 A1/2B7/9C3D7
A1/2B7/9C3D7A solid sphere of uniform density and radius R applies a gravitational force of attraction equal to F1 on a particle placed at P, distance 2R from the centre O of the sphere. A spherical cavity of radius R/2 is now made in the sphere as shown in figure. The particle with cavity now applies a gravitational force F2 on same particle placed at P. The radio F2/F1 will be
 A12B79C3D7
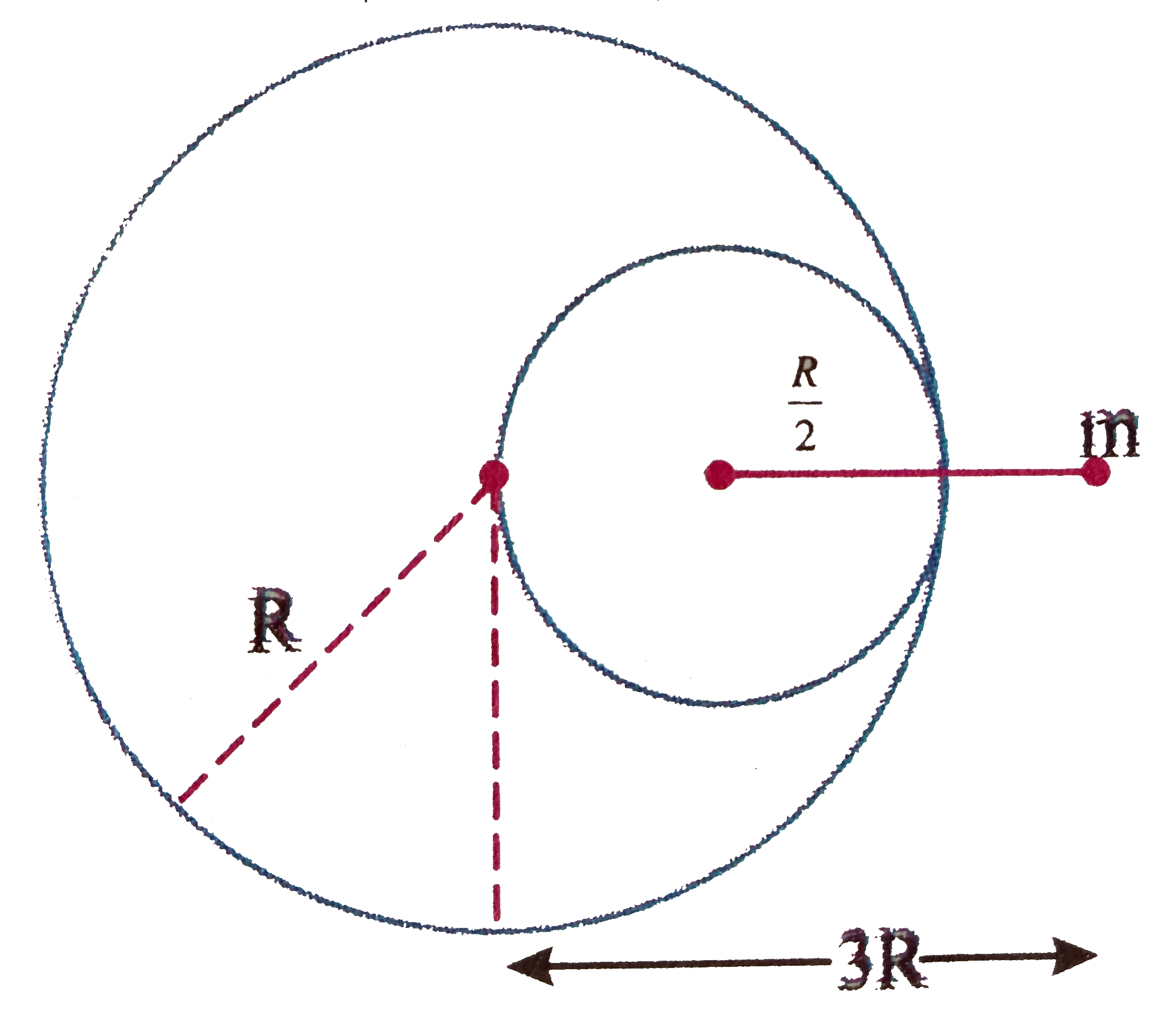
A12B79C3D7A solid sphere of radius R gravitationally attracts a particle placed at 3R form its centre with a force F1. Now a spherical cavity of radius (R2) is made in the sphere (as shown in figure) and the force becomes F2 The value of F1:F2 is:
 A25:36B36:25C50:41D41:50
A25:36B36:25C50:41D41:50
A solid of radius 'R' is uniformly charged with charge density ρ in its volume. A spherical cavity of radius R2 is made in the sphere as shown in the figure. Find the electric potential at the centre of the sphere.

View SolutionA hemi-spherical cavity is created in solid sphere (of radius 2R) as shown in the figure. Then

View SolutionA hemispherical cavity of radius R is created in a solid sphere of radius 2R as shown in the figure . Then y -coordinate of the centre of mass of the remaining sphere is

View SolutionA solid sphere of mass M and radius R has a spherical cavity of radius R/2 such that the centre of cavity is at a distance R/2 from the centre of the sphere. A point mass m is placed inside the cavity at a distance R/4 from the centre of sphere. The gravitational force on mass m is
View SolutionThe figure represents a solid uniform sphere of mass M and radius R. A spherical cavity of radius r is at a distance a from the centre of the sphere. The gravitational field inside the cavity is

View Solution
