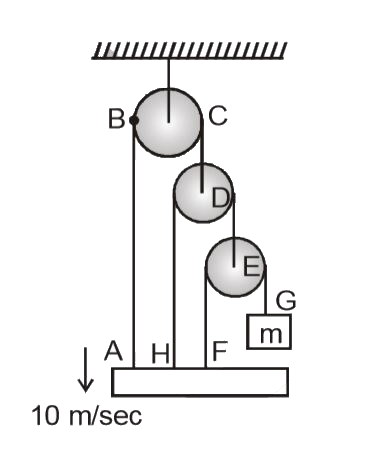
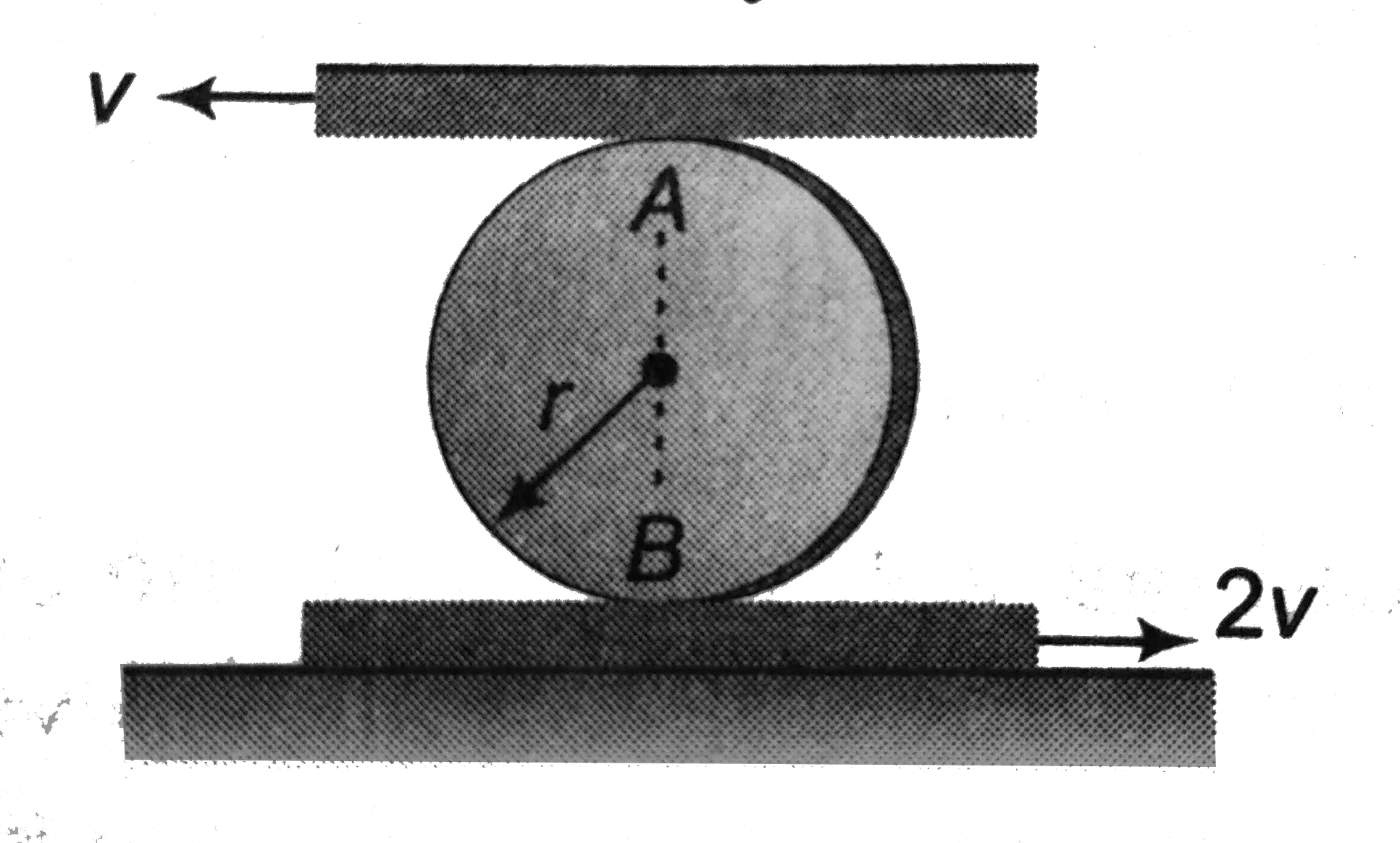
Due to slippoing points A and B on the rim of the disk have the velocities shown. Determine the velocities of the centre point C and point F at this instant.

v+Rω=1.5
and Rω−v=3.0
From Eq. (i) and (ii) we have
Rω=2.25m/s and v=−0.75m/s
thus velocity of point C is 0.75 m/s (towards left).
VF=√v2+(Rω)2+2v(Rω)cos(90+30)
=√0.5625+5.0625+2×0.75×2.25×(−12)
1.98m/s
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Subjective Questions
2 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2
1 Video
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
Similar Questions
Knowledge Check
The velocity of point A on the rod is 2ms−1 (leftwards) at the instant shown in fig. The velocity of the point B on the rod at this instant is
 A2√3ms−1B1ms−1C12√3ms−1D√32ms−1
A2√3ms−1B1ms−1C12√3ms−1D√32ms−1The points 'A' and 'B' of a disc are pulled with velocity 'V' as shown in the diagram. Then the velocity of centre 'C' of disc (here the points A, B, C lie on same diameter) will be
 .A0BV2CV3D2V3
.A0BV2CV3D2V3A circular disc rolls on a horizontal floor without slipping and the centre of the disc moves with a unifonn velocity v. Which of the following values the velocity at a point on the rim of the disc can have?
AvB−vC2vDzero
Consider a rigid body rotating in a plane. We wish to determine the angular velocity of the rigid body given the known velocities of points A and B on the rigid body. These velocities are parallel and pointing in the same direction. The line joining points A and B is perpendicular to the direction of the velocities. The figure below illustrates the set up of the problem.
Note that lC is the intersection of the line passing through points A and B, and the line joining the tip of the vectors vAandvB

View SolutionA wheel rolls purely on ground. Find a point on the periphery of a body which has a velocity equal to the velocity of the centre of mass of the body.
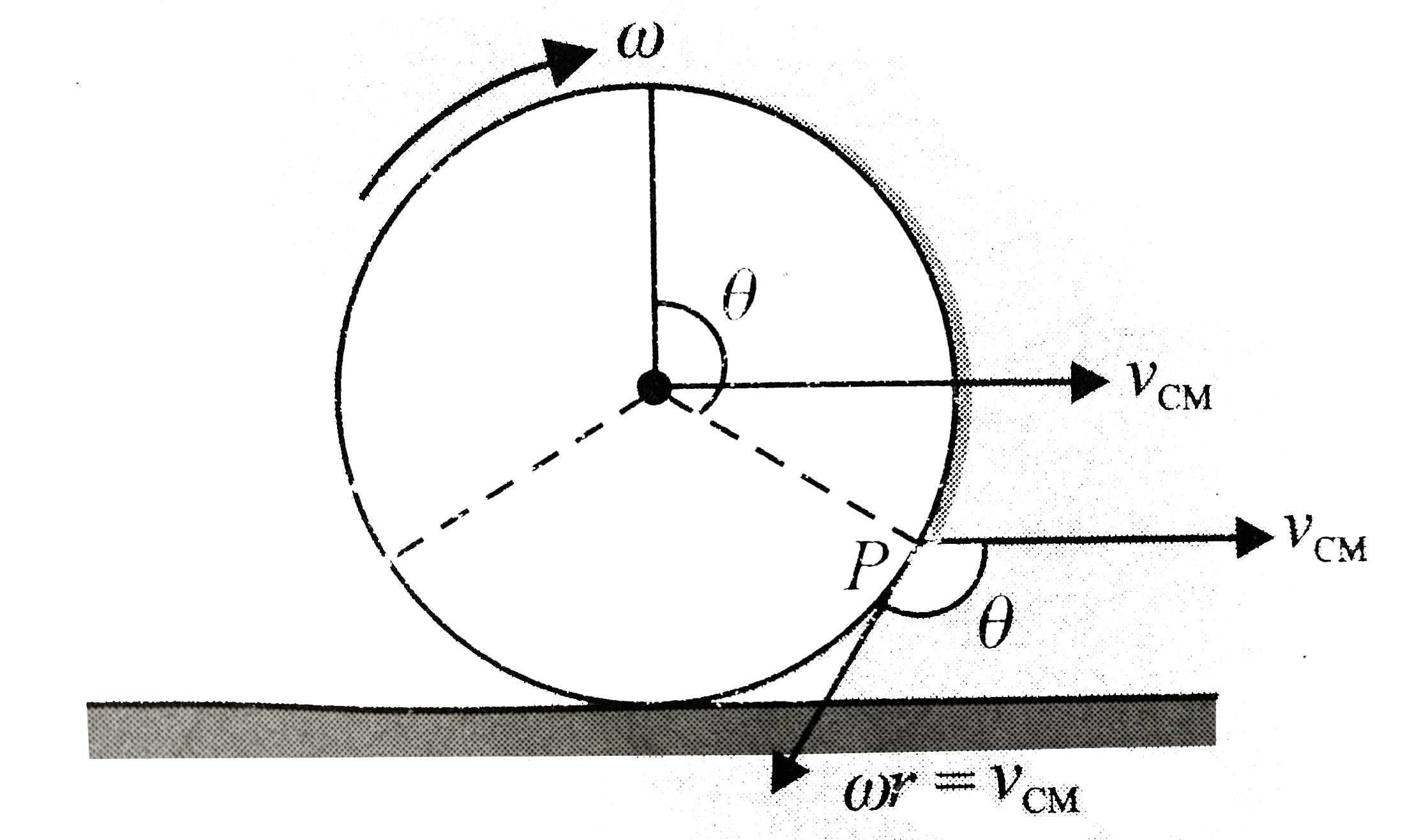
View SolutionA circular disc rolls on a horizontal floor without slipping and the center of the disc moves with a uniform velocity v. Which of the following values of the velocity at a point on the rim of the disc can have?
View SolutionA unifrom solid disk of radius R and mass M is free to rotate on a frictionless pivot through a point on its rim. If the disk is released from rest in the position shown in figure. The speed of the lowest point on the disk in the dashed position is.
 .
.
View SolutionA sphere of radius R is in contact with a wedge. The point of contact is R/5 from the ground as shown in the figure. Wedge is moving with velocity 20m/s, then the velocity of the sphere at this instant will be
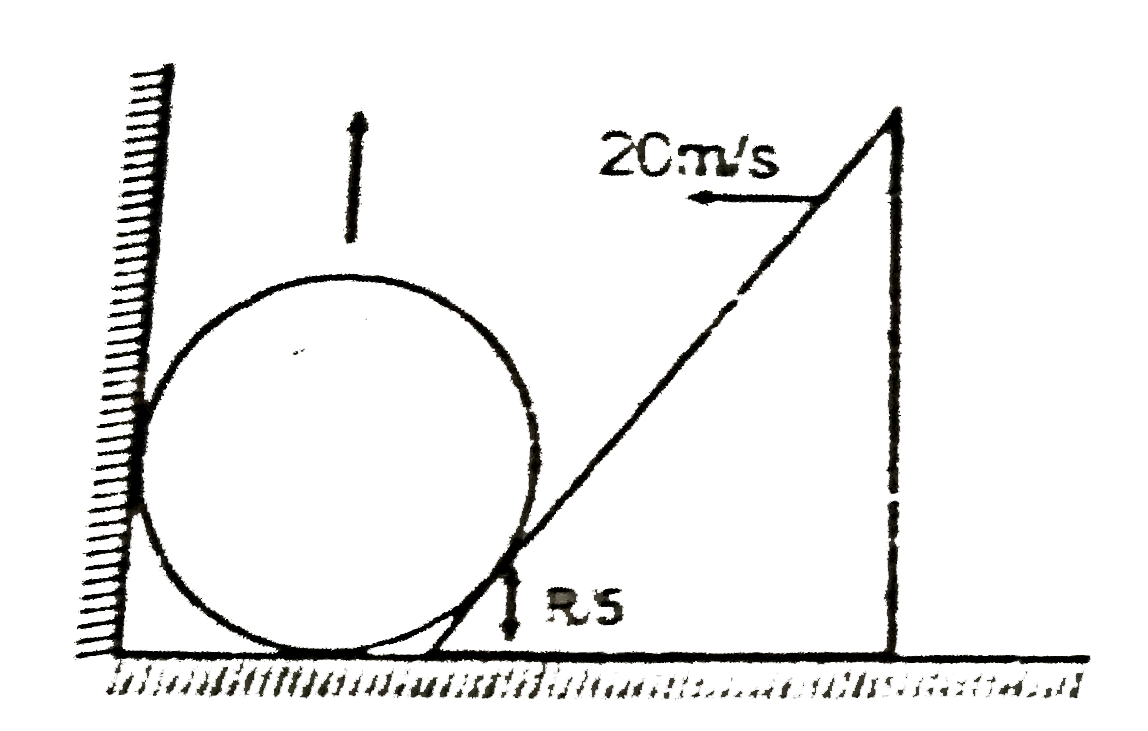
View Solution