
Find moment of inertia of a thin sheet of mass M in the shape of an equilateral triangle about an axis as shown in figure. The length of each side is L
3ML2/8
3√3ML2/8
7ML2/8
none of these
The correct Answer is:A
Step by step video & text solution for Find moment of inertia of a thin sheet of mass M in the shape of an equilateral triangle about an axis as shown in figure. The length of each side is L by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 1 Subjective
32 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2 Single Correct
26 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Assertion And Reason
11 Videos
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
Similar Questions

Find the moment of inertia of the rod AB about an axis yy as shown in figure. Mass of the rod is m and length is l.
View SolutionThree particles, each of mass m are situated at the vertices of an equilateral triangle ABC of side l (as shown in the figure).
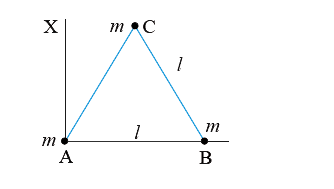
The moment of inertia of the system about a line AX perpendicular to AB and in the plane of ABC, will be:
View Solution
Knowledge Check
The moment of inertia of a thin sheet of mass M of the given shape about the specified axis is
 A(3/2)MR2B(3/4)MR2CMR2(1+1/√2)DMR2/(2√2)
A(3/2)MR2B(3/4)MR2CMR2(1+1/√2)DMR2/(2√2)Find the moment of inertia of a hemisphere of mass M and radius R shown in the figure, about an axis AA' tangential to the hemisphere.
 AI=(920)mR2BI=(1320)mR2CI=(720)mR2DI=(320)mR2
AI=(920)mR2BI=(1320)mR2CI=(720)mR2DI=(320)mR2The moment of inertia of a thin sheet of mass M of the given shape about the specified axis is ( axis and sheet both are in same plane :)
 A712Ma2B512Ma2C13Ma2D112Ma2
A712Ma2B512Ma2C13Ma2D112Ma2
The moment of inertia of a thin rod of mass M and length L about an axis perpendicular to the rod at a distance L/4 from one end is
View SolutionA thin semi circular cylindrical shell has mass M and radius R. Find its moment of inertia about a line passing through its centre of mass parallel to the axis (shown in figure) of the cylinder.

View Solution
Three rods each of mass m and length l are joined together to form an equilateral triangle as shown in figure. Find the moment of inertial of the system about an axis passig through its centre of mass and perpendicular to the plane of the particle.
View SolutionA current of 10A is flowing in a equilateral triangle of side length l=1M as shown in figure. The magnetic field at center of triangle is:
_2019_CBT6_E01_040_Q01.png)
View SolutionMoment of inertia of a cylindrical shell of mass M, radius R and length L about its geometrical axis would be -
View Solution