For the same total mass, which of the following will have the largest moment of inertia about an axis passing through the centre of mass and perpendicular to the plane of the body
a disc of radius R
a ring of radius R
a square lamina of side 2 R
four rods forming a square of side 2R
The correct Answer is:D
To determine which of the given shapes has the largest moment of inertia about an axis passing through the center of mass and perpendicular to the plane of the body, we will calculate the moment of inertia for each shape. Let's denote the total mass of each shape as m.
Step 1: Moment of Inertia of the Disc
The moment of inertia I of a disc about an axis through its center and perpendicular to its plane is given by:
Idisc=12mr2
Step 2: Moment of Inertia of the Ring
The moment of inertia I of a ring about an axis through its center and perpendicular to its plane is given by:
Iring=mr2
Step 3: Moment of Inertia of the Square Lamina
For a square lamina with side length 2r, the moment of inertia about an axis through its center and perpendicular to its plane is given by:
Isquare=16m(2r)2=23mr2
Step 4: Moment of Inertia of the Square Formed by Four Rods
For a square formed by four rods, we can calculate the moment of inertia using the parallel axis theorem. Each rod has a mass of m4 and length 2r. The moment of inertia of one rod about its center is:
Irod=112(m4)(2r)2=mr212
Using the parallel axis theorem, the distance from the center of the square to the center of each rod is r. Thus, the total moment of inertia for one rod is:
Itotal, rod=Irod+(m4)r2=mr212+mr24=mr212+3mr212=4mr212=mr23
Since there are four rods, the total moment of inertia for the square is:
Isquare of rods=4⋅mr23=4mr23
Step 5: Comparing the Moments of Inertia
Now we can compare the moments of inertia calculated:
1. Disc: 12mr2
2. Ring: mr2
3. Square Lamina: 23mr2
4. Square of Rods: 43mr2
Conclusion
From the calculations:
- Moment of inertia of the disc: 12mr2
- Moment of inertia of the ring: mr2
- Moment of inertia of the square lamina: 23mr2
- Moment of inertia of the square formed by four rods: 43mr2
The largest moment of inertia is from the square formed by four rods, which is 43mr2.
Thus, the answer is the square formed by four rods.
The moment of inertia I of a disc about an axis through its center and perpendicular to its plane is given by:
Idisc=12mr2
The moment of inertia I of a ring about an axis through its center and perpendicular to its plane is given by:
Iring=mr2
For a square lamina with side length 2r, the moment of inertia about an axis through its center and perpendicular to its plane is given by:
Isquare=16m(2r)2=23mr2
For a square formed by four rods, we can calculate the moment of inertia using the parallel axis theorem. Each rod has a mass of m4 and length 2r. The moment of inertia of one rod about its center is:
Irod=112(m4)(2r)2=mr212
Using the parallel axis theorem, the distance from the center of the square to the center of each rod is r. Thus, the total moment of inertia for one rod is:
Itotal, rod=Irod+(m4)r2=mr212+mr24=mr212+3mr212=4mr212=mr23
Since there are four rods, the total moment of inertia for the square is:
Isquare of rods=4⋅mr23=4mr23
Now we can compare the moments of inertia calculated:
1. Disc: 12mr2
2. Ring: mr2
3. Square Lamina: 23mr2
4. Square of Rods: 43mr2
From the calculations:
- Moment of inertia of the disc: 12mr2
- Moment of inertia of the ring: mr2
- Moment of inertia of the square lamina: 23mr2
- Moment of inertia of the square formed by four rods: 43mr2
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 1 Subjective
32 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2 Single Correct
26 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Assertion And Reason
11 Videos
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
Similar Questions
A ring and a circular disc of different materials have equal masses and equal radii. Which one will have a larger moment of inertia about an axis passing through its centre of mass perpendicular to its plane ?
View SolutionA square of a side a is cut from a square of side 2a as shown in the figure. Mass of this square with a hole is M. Then its moment of inertia about an axis passing through its centre of mass and perpendicular to its plane will be
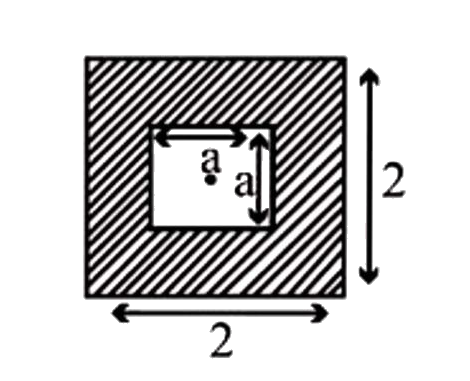
View Solution
Knowledge Check
For the same total mass which of the following will have the largest moment of inertia about an axis passing through its centre of mass and perpendicular to the plane of the body.
Aa disc of radius aBa ring of radius oaCa square lamina of side 2aDfour rods forming a square of side 2a.For the same total mass, which of the following will have the largest moment of inertia about an axis passing through the centre of mass and perpendicular to the plane of the body
Aa ring o radius lBa disc of radius lCa square lamina of side 2lDFour rods forming square of side 2lA uniform thin bar of mass 6m and length 12L is bend to make a regular hexagon. Its moment of inertia about an axis passing through the centre of mass and perpendicular to the plane of the hexagon is :
A20mL2B6mL2C125mL2D30mL2
A uniform thin bar of mass 6m and length 12L is bent to make a regular hexagon. Its moment of inertia about an axis passing through the centre of mass and perpendicular to the plane of hexagon is
View SolutionThree bodies have equal massses m. Body A is solid cylinder of radius R, body B is a square lamina of side R, and body C is solid sphere of radius R. Which body has the smallest moment of inertia about an axis passing through their centre of mass and perpendicular to the plane (in case of lamina).
View SolutionThe moment of inertia of a copper disc, rotating about an axis passing through its centre and perpendicular to its plane
View SolutionWhich of the following has the largest moment of inertia about the central axis if all have equal mass and radii ?
View SolutionMoment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
View Solution
