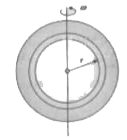
Find the moment of inertia of a solid sphere of mass and radias about an axis XX shown in figure.
A
B
C
D
Video Solution
Text Solution
The correct Answer is:A

From theorem of parallel axis
Radius of gyration
|
Topper's Solved these Questions
- ROTATIONAL MECHANICSBook:DC PANDEYChapter:ROTATIONAL MECHANICSExercise:Solved Examples
Explore 25 Videos
- ROTATIONAL MECHANICSBook:DC PANDEYChapter:ROTATIONAL MECHANICSExercise:Miscellaneous Examples
Explore 2 Videos
- ROTATIONBook:DC PANDEYChapter:ROTATIONExercise:(C) Chapter Exercises
Explore 39 Videos
- ROTATIONAL MOTIONBook:DC PANDEYChapter:ROTATIONAL MOTIONExercise:Integer Type Questions
Explore 17 Videos
Similar Questions
Knowledge Check
The moment of inertia of a solid sphere of mass ‘M' and radius 'R' about a tangent to the sphere is
A25MR2B63MR2C45MR2D75MR2The moment of inertia of a solid sphere of mass M and radius R about its diameter is I. The moment of inertia of the same sphere about a tangent parallel to the diameter is
A5 IB7 IC2.5 ID3.5 IFind the moment of inertia of a hemisphere of mass M and radius R shown in the figure, about an axis AA' tangential to the hemisphere.
 AI=(920)mR2BI=(1320)mR2CI=(720)mR2DI=(320)mR2
AI=(920)mR2BI=(1320)mR2CI=(720)mR2DI=(320)mR2
The moment of inertia of a ring of mass M and radius R about PQ axis will be :-
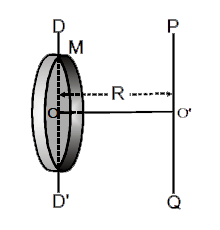
View SolutionThe moment of inertia of a ring of mass M and radius R about PQ axis will be

View SolutionFind moment of inertia of a uniform solid sphere (mass m, radius r) about a tangent.
View SolutionFind the moment of inertia of a solid cylinder of mass M and radius R about a line parallel to the axis of the cylinder and on the surface of the cylinder.
View SolutionFind the moment of inertia of a uniform sphere of mass m and radius R about a tangent if the spheres (1) solid (ii) hollow?
View Solution