The coefficient of restitution between a snooker ball and the side cushion is 13. If the ball hits the cushion and then rebounds at right angles to its original direction, show that the angles made with the side cushion by the direction of motion before and after impact are 60∘ and 30∘ respectively.
To solve the problem, we need to analyze the collision of the snooker ball with the side cushion using the concept of the coefficient of restitution. The coefficient of restitution (e) is defined as the ratio of the relative velocity of separation to the relative velocity of approach along the line of impact.
1. Understanding the Problem:
- A snooker ball strikes the cushion and rebounds at right angles to its original direction.
- The coefficient of restitution (e) between the ball and the cushion is given as 13.
2. Setting Up the Coordinate System:
- Let's assume the cushion is vertical and the ball approaches it at an angle θ1 with respect to the normal (perpendicular) to the cushion.
- After the collision, the ball rebounds at an angle θ2 with respect to the normal.
3. Using the Coefficient of Restitution:
- The coefficient of restitution is defined as:
e=Velocity of separationVelocity of approach
- In terms of angles, we can express the velocities in terms of the angles with the normal:
e=v2cos(θ2)v1cos(θ1)
- Here, v1 is the speed of the ball before impact, and v2 is the speed after impact.
4. Substituting the Given Coefficient:
- We know e=13, so we can write:
13=v2cos(θ2)v1cos(θ1)
5. Analyzing the Angles:
- Given that the ball rebounds at right angles to its original direction, we can set θ2=90∘−θ1.
- Thus, we can express cos(θ2) as sin(θ1).
6. Setting Up the Equation:
- Substituting cos(θ2)=sin(θ1) into the equation gives:
13=v2sin(θ1)v1cos(θ1)
7. Using the Right Triangle Relationships:
- From the right triangle formed by the angles, we have:
tan(θ1)=sin(θ1)cos(θ1)
- Therefore, we can express sin(θ1) and cos(θ1) in terms of tan(θ1).
8. Finding the Angles:
- After solving the equations, we find:
θ1=60∘andθ2=30∘
Conclusion:
Thus, the angles made with the side cushion by the direction of motion before and after impact are 60∘ and 30∘, respectively.
- A snooker ball strikes the cushion and rebounds at right angles to its original direction.
- The coefficient of restitution (e) between the ball and the cushion is given as 13.
- Let's assume the cushion is vertical and the ball approaches it at an angle θ1 with respect to the normal (perpendicular) to the cushion.
- After the collision, the ball rebounds at an angle θ2 with respect to the normal.
- The coefficient of restitution is defined as:
e=Velocity of separationVelocity of approach
- In terms of angles, we can express the velocities in terms of the angles with the normal:
e=v2cos(θ2)v1cos(θ1)
- Here, v1 is the speed of the ball before impact, and v2 is the speed after impact.
- We know e=13, so we can write:
13=v2cos(θ2)v1cos(θ1)
- Given that the ball rebounds at right angles to its original direction, we can set θ2=90∘−θ1.
- Thus, we can express cos(θ2) as sin(θ1).
- Substituting cos(θ2)=sin(θ1) into the equation gives:
13=v2sin(θ1)v1cos(θ1)
- From the right triangle formed by the angles, we have:
tan(θ1)=sin(θ1)cos(θ1)
- Therefore, we can express sin(θ1) and cos(θ1) in terms of tan(θ1).
- After solving the equations, we find:
θ1=60∘andθ2=30∘
Thus, the angles made with the side cushion by the direction of motion before and after impact are 60∘ and 30∘, respectively.
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Solved Examples
13 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Type 1
1 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
- CIRCULAR MOTIONBOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Medical entrances s gallery
19 Videos
Similar Questions
A sphere of mass m, impinges obliquely on a sphere, of mass M, which is at rest. Show that, if m=eM, the directions of motion of the sphere after impact are at right angles.
View SolutionConsider an oblique elastic collision between a moving ball and a stationary ball of the same mass. Both the balls move with the same speed after the collision. After the collision, the angle between the directions of motion of two balls is x degree. Find the value of x.
View Solution
Knowledge Check
The coefficient of restitution for a body is e=13. At what angle the body must be incident on a perfectly hard plane so that the angle between the direction before and after the impact be at right angles:
A37∘B60∘C45∘D30∘A ball of mass m moving with a velocity v undergoes an oblique elastic collision with another ball of the same mass m but at rest. After the collision if the two balls move with the same speeds , the angle between their directions of motion will be:
A30∘B60∘C120∘D90∘Suppose a ball is projected with speed u at an angle α with horizontal. It collides at some distance with a wall parallel to y-axis.
Let vx and vy be the components of its velocity along x and y-directions at the time of impact with wall. Coefficient of restitution between the ball and the wall is e. Component of its velocity along y-diection (common tangent) vy will remain unchanged while component of its velocity along x -direction (common normal) vx will become evx is opposite direction.
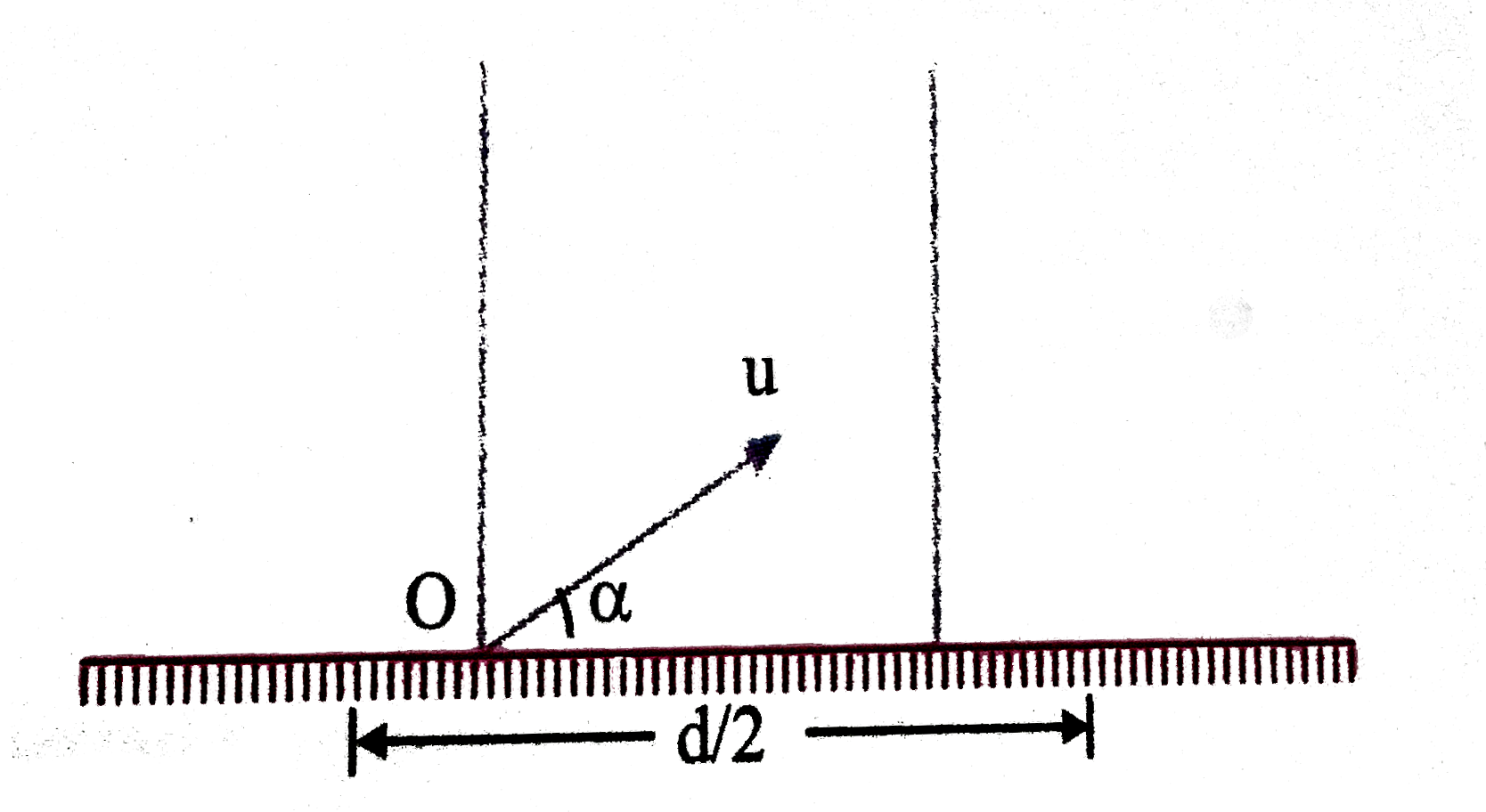
The situation shown in the figure a small ball is projected at an angle α between two vertical walls such that in the absence of the wall its range would have been 5d. Given that all the collisions are perfectly elastic (for first and second problems), the walls are supposed to be very tall.
The total time taken by the ball to come back to the ground (if collision is inelastic) isA>2usinαgB<2usinαgC=2usinαgD=2ucosαg
A ball is projected from point A in horizontal direction with a velocity of u=28m/s. It hits the incline plane at point B and rebounds. Show that whatever be the coefficient of restitution between the ball and the incline, the ball will always hit the incline for the second time at a point above B (i.e., it will not hit the incline below B). Assume the incline to be smooth and take g=10m/s2[sin37∘=35]
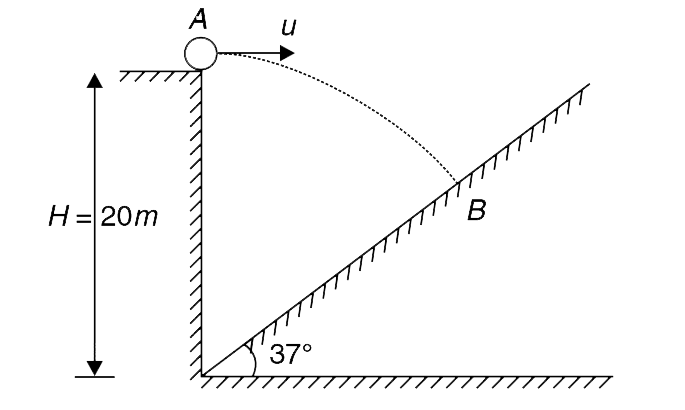
View SolutionA ball , moving with a speed of 10√3m/s , strikes an identical stationary ball such that after the collision , the direction of each ball makes an angle of 30∘with the original line of motion. The speeds of two balla after the collision are , respectively.
View SolutionA ball is thrown with velocity 8ms−1 making an angle 60∘ with the horizontal.Its velocity will be perpendicular to the direction of initial velocity of projection after a time of
View SolutionTwo balls with masses in the ratio of 1:2 moving in opposite direction have a head-on elastic collision. If their velocities before impact were in the ration of 3:1, then velocities after impact will have the ratio :
View SolutionA ball is dropped from a height of 45m from the ground. The coefficient of restitution between the ball and the ground is 23. What is the distance travelled by the ball in 4th second of its motion. Assume negligible time is spent in rebounding. Let g=10ms2
View Solution
