A 0.500kg block is attached to a spring with length 0.60m and force constant k=40.0N/m. The mass of the spring is negligible. You pull the block to the right along the surgace with a constant horizontal force F=20.0N. (a) What is the block's speed when the block reaches point B,which is 0.25m to the right of right of point A? (b) What the block reaches point B, you let go off the block. In the subsequent motion, how close dies the block get to the wall where the lift end of the spring is attached? Neglect size of block and friction.
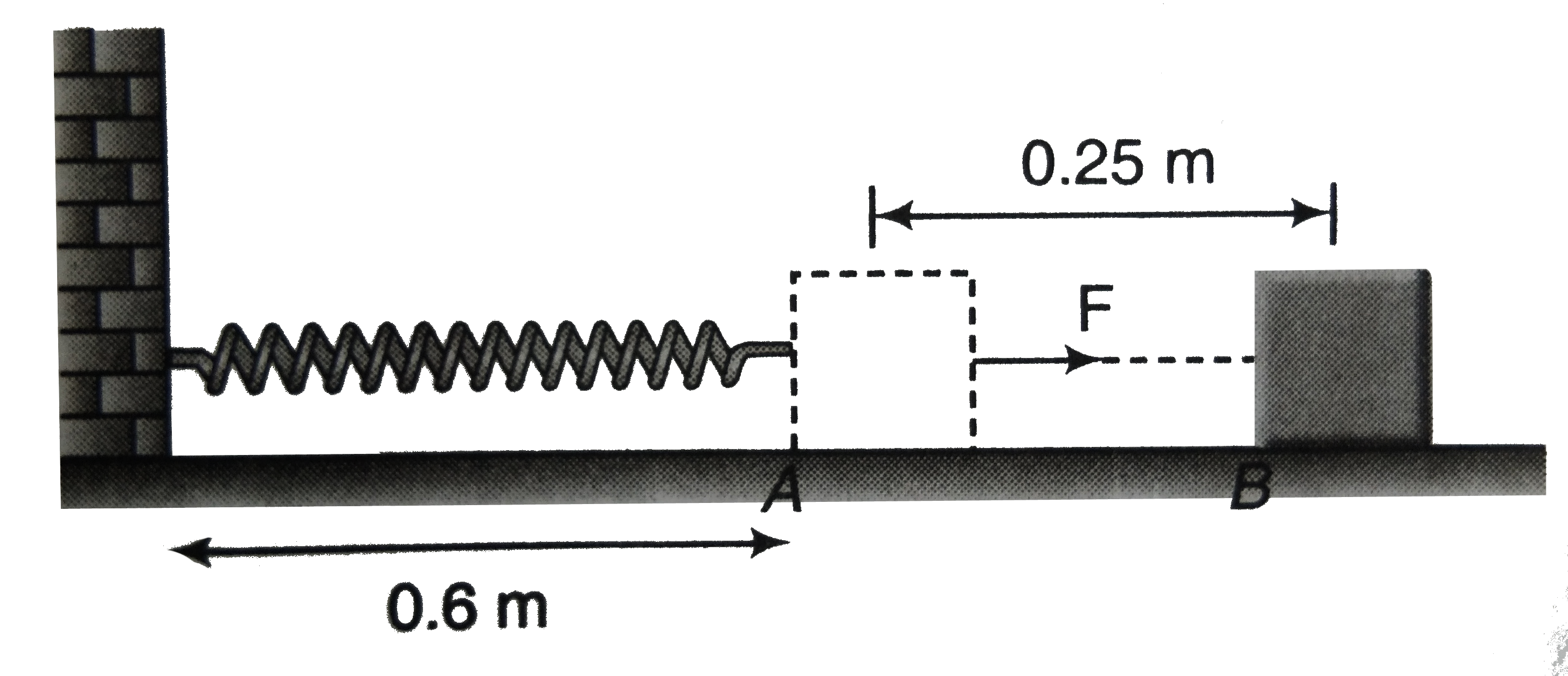 .
.
The correct Answer is:A, B, C
(a) From work energy theorem,
Work done by all forces = change in kinetic energy
∴Fx−12kx2=12mv2
∴v√2Fx−kx2m
Substituting the values we have,
v=√2×20×0.25−40×25×0.250.5
=√15m/s=3.87m/s
(b) From conservation of mechanical energy,
Ei=E(f)
or 12mv2i+12kx2i=12kx2f
or xf=√mv2ik+x2i
=√0.5×1540+(0.25)2
0.5m (compression
∴ Distance of block from the wall
=(0.6−0.5)m
=0.1m.
Topper's Solved these Questions
- WORK, ENERGY & POWERBOOK - DC PANDEYCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Comprehension Based
2 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEYCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 More Than One Correct
9 Videos
- WAVE MOTIONBOOK - DC PANDEYCHAPTER - WAVE MOTIONEXERCISE - Integer Type Question
11 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEYCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY
33 Videos
Similar Questions
The figure shows the variation of potential energy of a particle as a funcation pf x, the x-coordination of the region. It has been assumed that potential energy depends only on x. For all other values x,U is zero. i.e. forx<−10 and x>15,U=0.
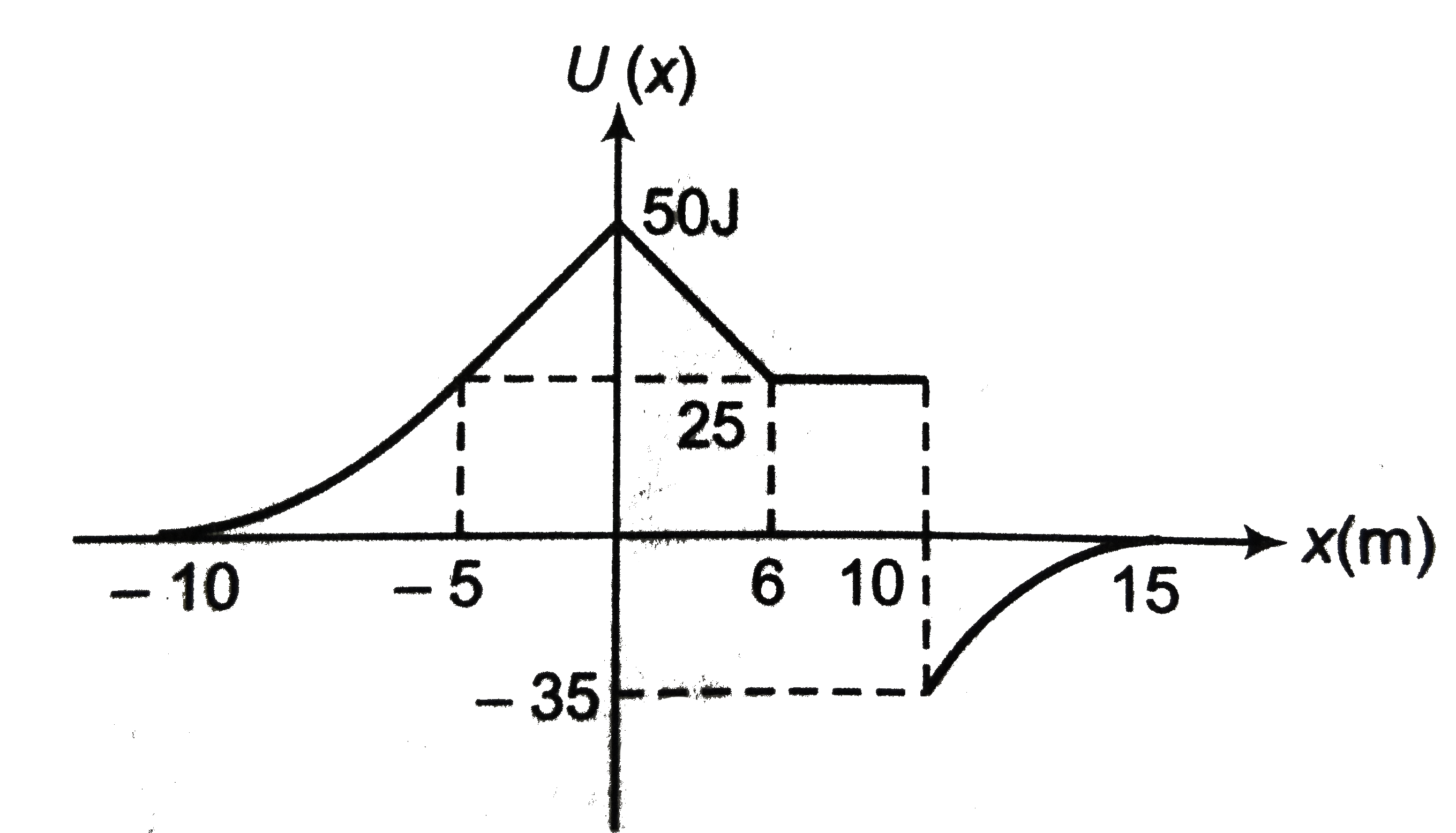
If total mechanical energy of the particle is 25J, then it can found in the region
View SolutionThe potential energy of a particle of mass 5 kg moving in xy-plane is given as U=(7x+24y) joule, x and y being in metre. Initially at t=0, the particle is at the origin (0,0) moving with velovity of (8.6ˆi+23.2ˆj)ms1, Then
View SolutionTwo wires of same material of radii 2r and r are welded together end to end The combination is used as a sonometer wire and is kept under tension T. The welded point lies midway between the bridges. What wil be the ratio of the number of loops formed in the wires, such that the joint is node when the stationary waves are set up in the wire?
View SolutionA body of mass 1kg begins to move under the action of a time dependent force →F=(2tˆI+3t2ˆj)N, where ˆi and ˆj are unit vectors along x-and y-axes. What power will be developed by the force at the time t ?
View SolutionA block of mass m is connected to another block of mass M by a spring (massless) of spring constant k. The block are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unstretched. Then a constant force F starts acting on the block of mass M to pull it. Find the force of the block of mass M.
View SolutionA block of mass m = 2 kg is connected to a spring of force constant k = 50 n//m . Initially the block is at rest and the spring has natural length . A constant force f = 60 N , is applied horizontally towards right, the maximum speed of the block (in m//s will be (neglect frication).
View SolutionA block of mass 'm' is connected to another block of mass 'M' by a spring (massless) of spring constant 'k' The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unstretched Then a constant force 'F' starts acting on the block of mass 'M' to pull it. Find the force on the block of mass 'm' :
View SolutionA block of mass m, lying on a smooth horizontal surface, is attached to a spring (of negligible mass) of spring constant k. The other end of the spring is fixed, as shown in the figure. The block is initally at rest in its equilibrium position. If now the block is pulled withe a constant force F, the maximum speed of the block is :

View SolutionA block of mass m, lying on a smooth horizontal surface, is attached to a spring (of negligible mass) of spring constant k. The other end of the spring is fixed, as shown in the figure. The block is initally at rest in its equilibrium position. If now the block is pulled withe a constant force F, the maximum speed of the block is :
View Solutionm द्रव्यमान का एक ब्लॉक, M द्रव्यमान के दूसरे ब्लॉक से एक द्रव्यमान रहित तथा स्प्रिंग नियतांक K की स्प्रिंग से बँधा है | ब्लॉक चिकने क्षैतिज तल पर रखे हैं | प्रारम्भ में ब्लॉक विरामावस्था में है तथा स्प्रिंग बिना खिंची है | अब यदि M द्रव्यमान के ब्लॉक को एक नियत बल f लगाकर खींचा जाता है तो m द्रव्यमान के ब्लॉक पर लगा बल होगा :
View Solutionद्रव्यमान के एक ब्लॉक को द्रव्यमान M के दूसरे ब्लॉक में स्प्रिंग नियतांक की स्प्रिंग ( द्रव्यमान नगण्य ) द्वारा जोड़ दिया जाता है । ब्लॉक एक चिकने समतल पर रखे हुए हैं । प्रारंभ में ब्लॉक स्थिर है तथा स्प्रिंग सामान्य स्थिति में है, तब द्रव्यमान M के ब्लॉक को एक नियत बल f द्वारा खींचा जाता है । द्रव्यमान m के ब्लॉक पर आरोपित बल होगा -
View SolutionA block of mass 'm' is connected to another block of mass 'M' by a spring (massless) of spring constant 'k'. The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unstretched. Then a constant force 'F' starts acting on the block of mass 'M' to pull it. Find the force on the block of mass 'm'.
View SolutionA 2.0 - kg block executes SHM while attached to a horizontal spring of spring constant 200N/m. The maximum speed of the block as it slides on a horizontal frictionless surface is 3.0m/s.
What is the amplitude of the block's motion?
View SolutionA block of mass m is connected to another block of mass M by a spring (massless) of spring constant k. The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unstretched. Then a constant force F starts acting on the block of mass M to pull it. Find the force on the block of mass m.
View Solution3 किग्रा द्रव्यमान का एक ब्लॉक नगण्य द्रव्यमान की आदर्श स्प्रिंग में लटका है तथा स्प्रिंग में 0.2 मी का प्रसार उत्पन्न करता है।
(a) स्प्रिंग का बल नियंताक क्या है ?
(b) यदि ब्लॉक को नीचे खींच कर छोड़ दिया जाये तब इसका दोलन काल क्या होगा ?
View Solution
