Find the speed of both the blocks at the moment the block m2 hits the wall AB, after the blocks are released from rest. Given that m1=0.5kg and m2=2kg,(g=10m/s2)
 .
.
The correct Answer is:A, B, C
From conservation of energy ,
m2gh2=m1gh+(1)+12m1v1_(2)+12m2v(1)2
Here, v1=v2cosθ
:. 2×10×1=(0.5)(10)(√5−1)+12×0.5
xv22×(2√5)2+12×2×v22
∴20=6.18+0.2v22+v22
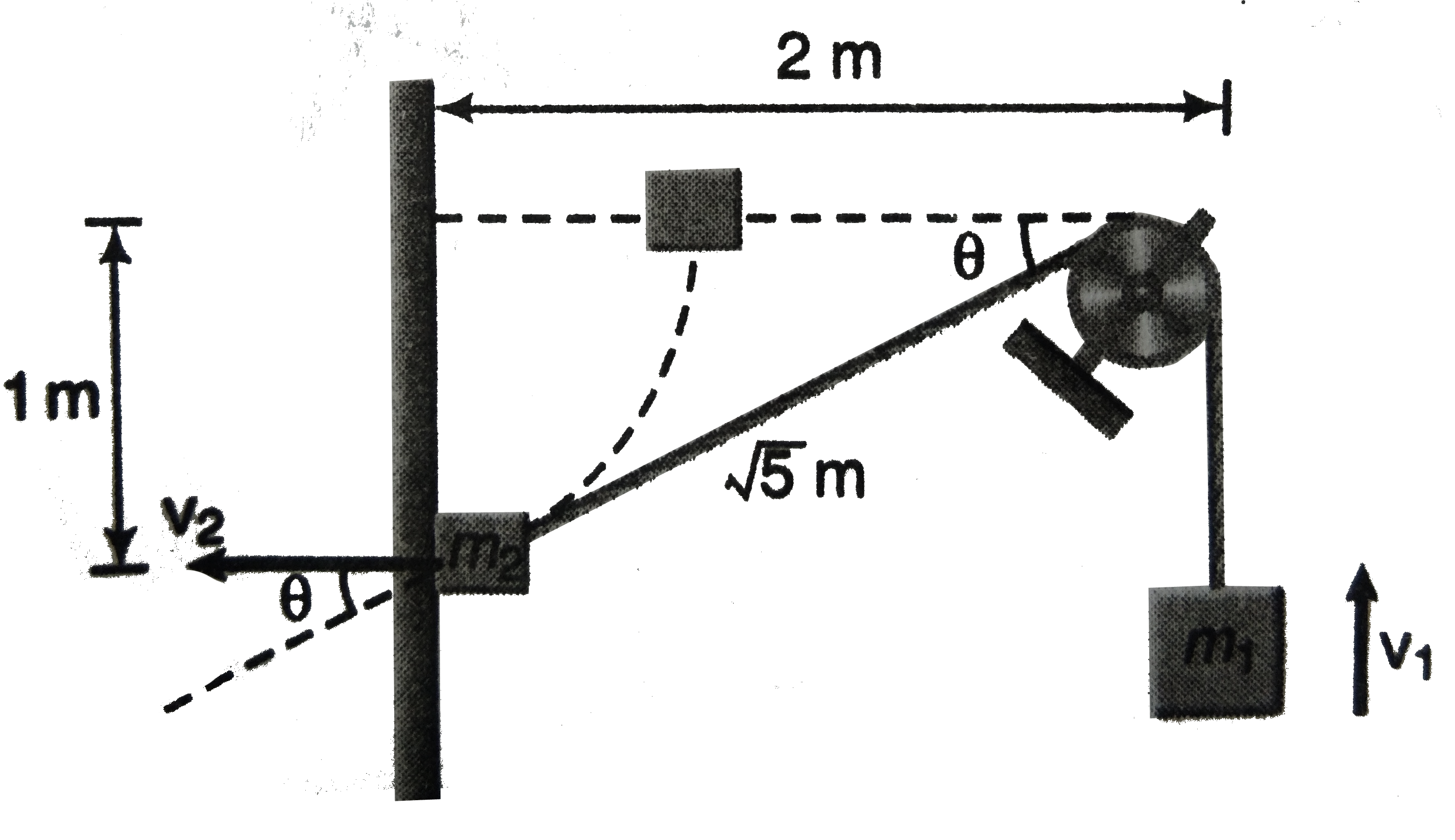
v2=3.39m/s
and v1=v2cosθ=2√5×3.39
or v1=3.03m/s,
Topper's Solved these Questions
- WORK, ENERGY & POWERBOOK - DC PANDEYCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Comprehension Based
2 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEYCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 More Than One Correct
9 Videos
- WAVE MOTIONBOOK - DC PANDEYCHAPTER - WAVE MOTIONEXERCISE - Integer Type Question
11 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEYCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY
33 Videos
Similar Questions
In the figure shown masses of the blocks A, B and C are 6kg, 2kg and 1kg respectively. Mass of the spring is negligibly small and its stiffness is 1000 N//m. The coefficient of friction between the block A snd the table is μ=0.8. Initially block C is held such that spring is in relaxed position. The block is released from rest. Find (g=10m/s2).

(a) the maximum distance moved by the kinetic C.
the acceleration of each block, when clongation in the spring is maximum.
View SolutionFind the acceleration of the two blocks . The system is initialy at rest and the friction are as shown in fig .Given mA=mB=10kg
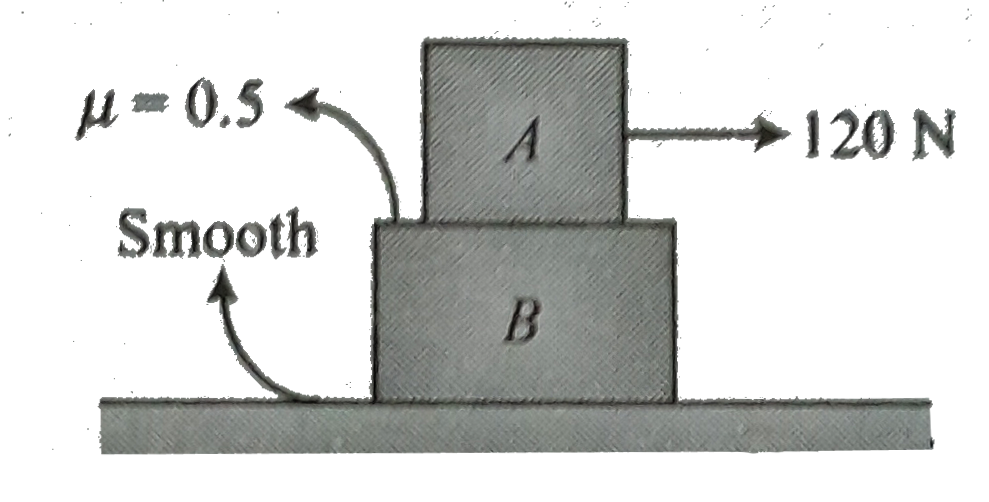
View Solution
Knowledge Check
A block of mass 2 kg rests on a rough horizontal plank , the coefficient of friction between the plank and block is 0.3. If the plank is pulled horizontally with a constant acceleration of 4m/s2 , the distance moved by the block on the plank in 5 second starting from rest (in m) is : (Take g = 10m/s2)
A5B10C25D50In the given figure, Find mass of the block A, if it remains at rest, when the system is released from rest. Pulleys and strings are massless. [g=10m/s2]
 AmB2mC2.5mD3m
AmB2mC2.5mD3m
A block of mass M=5kg is moving on a horizontal table and the coefficient of friction is μ=0.4. A clay ball of mass m=1kg is dropped on the block, hitting it with a vertical velocity of u=10 m/s. At the instant of hit, the block was having a horizontal velocity of v=2 m/s. After an interval of t, another similar clay ball hits the block and the system comes to rest immediately after the hit. Assume that the clay balls stick to the block and collision is momentary. Find t. Take g=10m/s2.

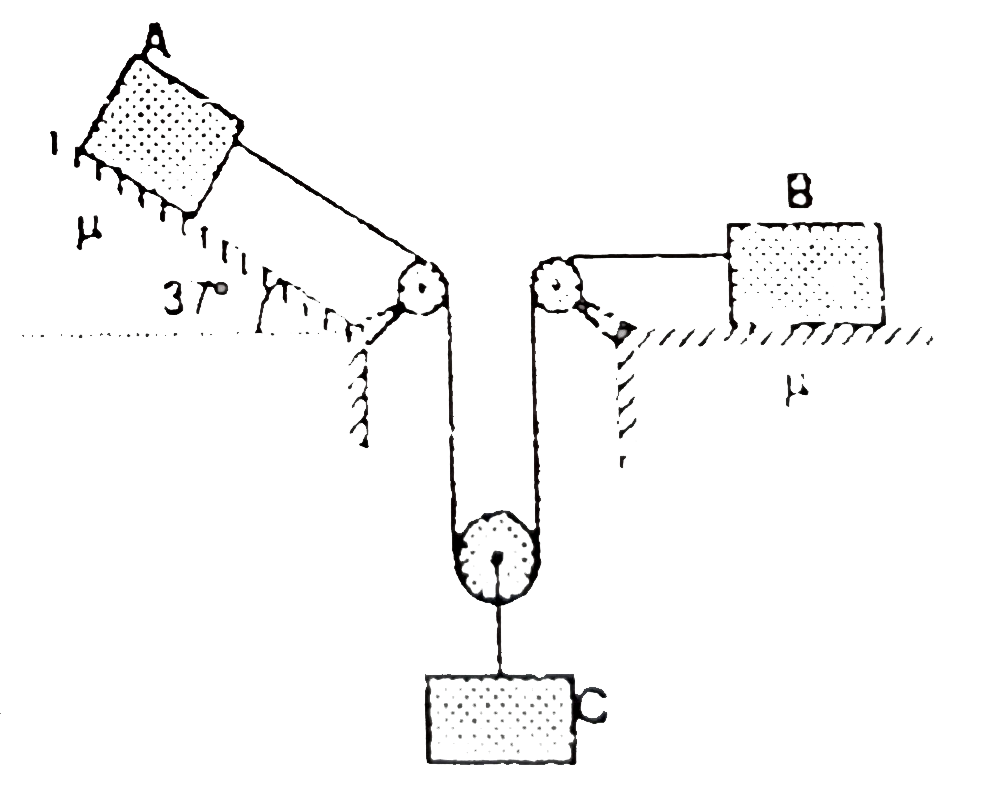
View SolutionIn the arrangement shown in the figure pulleys are small, light and frictionless, threads are inextensible and mass of blocks A, B and C is m1=5kg, m2=4kg and m3=2.5kg respectively and co-efficient of friction for both the planes is μ=0.50. Calculate the acceleration of block A (in m/s2) when the system is released from rest. (g=10m/s2)
View SolutionIn the figure shown co-efficient of friction between the block B and C is 0.4. There is no friction between the block C and hte surface on which it is placed. The system of blocks is released from rest in the shown situation. Find the distance moved by the block C when block A descends through a distance 2m. Given masses of the blocks are mA=3kg,mB=5kgandmC=10kg.

View SolutionA 5 kg block has a rope of mass 2 kg attached to its underside and a 3 kg block is suspended from the other end of the rope. The whole system is accelerated upward at 2m/s2 by an external force F0.
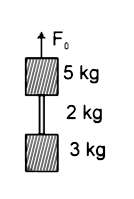
What is F0 ?
(g=10m/s2)
View SolutionThree blocks, placed on smooth horizontal surface are connected by ideal string and a disc shaped pulley of radius r, and mass m. Find the accelerations of the blocks. Masses of the blocks are given as M1=10kg,M2=5kg,M3=2kg,m=2kg.
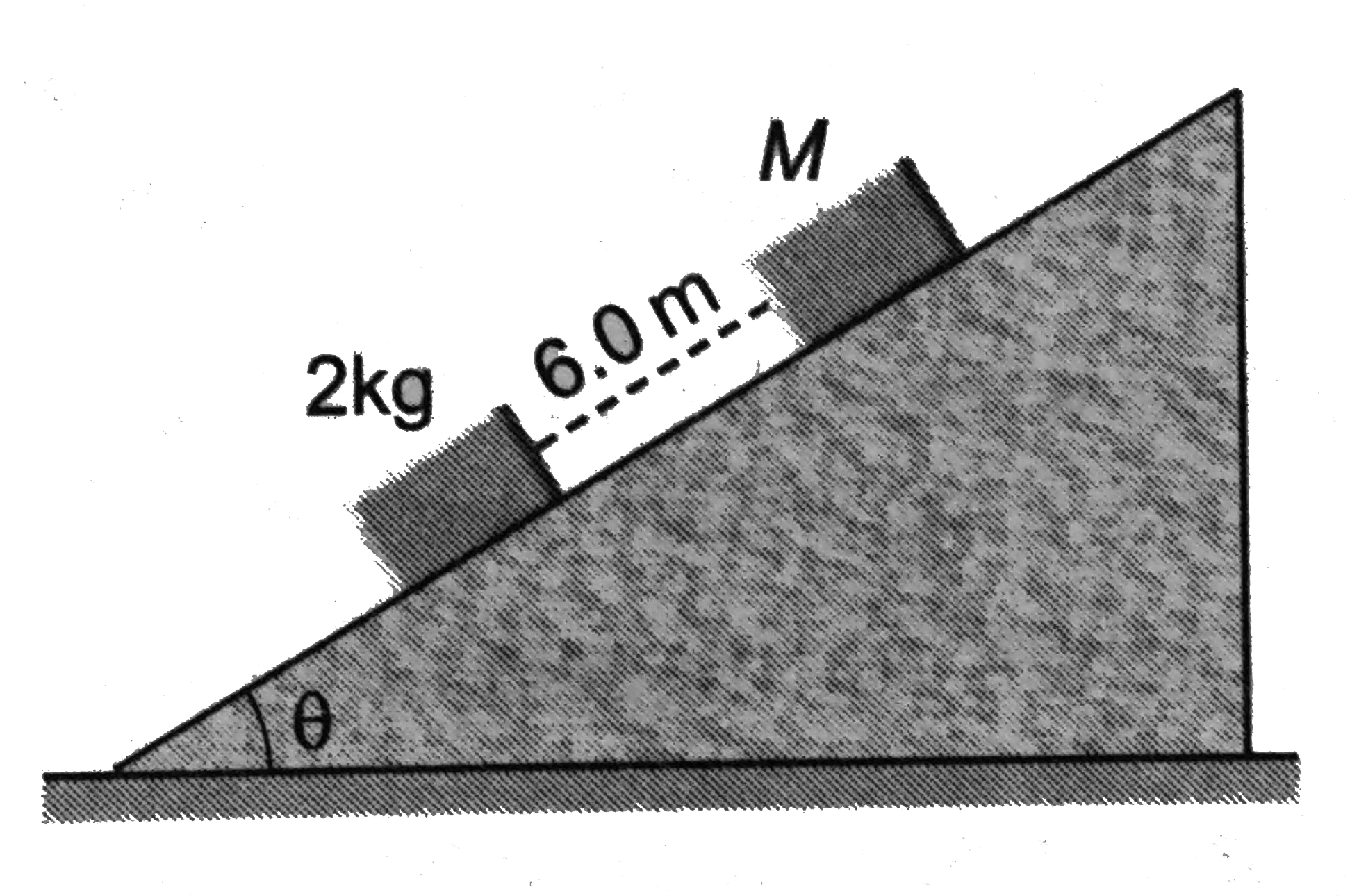
View SolutionTwo blocks of masses 2kg and M are at rest on an inclined plane and are separated by a distance of 6.0m as shown. The coefficient of friction between each block and the inclined plane is 0.25. The 2kg block is given a velocity of 10.0m/s up the inclined plane. It collides with M, comes back and has a velocity of 1.0m/s when it reaches its initial position. The other block M after the collision moves 0.5m up and comes to rest. Calculate the coefficient of restitution between the blocks and the mass of the block M.
[Take sinθ=tanθ=0.05 and g=10m/s2]
View Solution
