A spring mass system is held at rest with the spring relaxed at a height (h) above the ground. Determine the minimum value of (H) so that the systen has a tendency to rebound after hitting the ground. Given that the coefficient of restitution between (m2) and ground is zero.
 .
.
Conservation of mechanical energy give,
EA=EB
or 12m1v2=12kx2+m1gx
or 2m1gH=kx2+2m1gx

the lower block will rebounce when
x>m2gk,(kx=m2g)
Substituting, x=m2gk in Eq. (i), we get
2m1gH=k(m2gk)2+2m1g(m2gk)
or H=m2hk(m2+2m12m1)
Thus, Hmin=m2gk(m2+2m12m1a)
Topper's Solved these Questions
- WORK, ENERGY & POWERBook:DC PANDEYChapter:WORK, ENERGY & POWERExercise:Level 2 Comprehension Based
Explore 2 Videos
- WORK, ENERGY & POWERBook:DC PANDEYChapter:WORK, ENERGY & POWERExercise:Level 2 More Than One Correct
Explore 9 Videos
- WAVE MOTIONBook:DC PANDEYChapter:WAVE MOTIONExercise:Integer Type Question
Explore 11 Videos
- WORK, ENERGY AND POWERBook:DC PANDEYChapter:WORK, ENERGY AND POWERExercise:MEDICAL ENTRACES GALLERY
Explore 33 Videos
Similar Questions
Knowledge Check
A rubber ball drops from a height 'h'. After rebounding twice from the ground, it rises to h/2. The co-efficient of restitution is
A12B(12)1/2C(12)1/4D(12)1/6After falling from a height h and striking the ground twice, a ball rise up to the height [e = coefficient of restitution]
AheBhe2Che3Dhe4A ball is dropped from height 5m. The time after which ball stops rebounding if coefficient of restitution between ball and ground e=1/2, is
A1 secB2 secC3 secDinfinite
A rubber ball is dropped on the ground from a height of 1m. What is the height to which the ball will rebound, if the coefficient of restitution between the ball and the ground is 0.8?
View SolutionAn object of mass m is raised to a height 4h above ground level. Find the potential energy of the object.
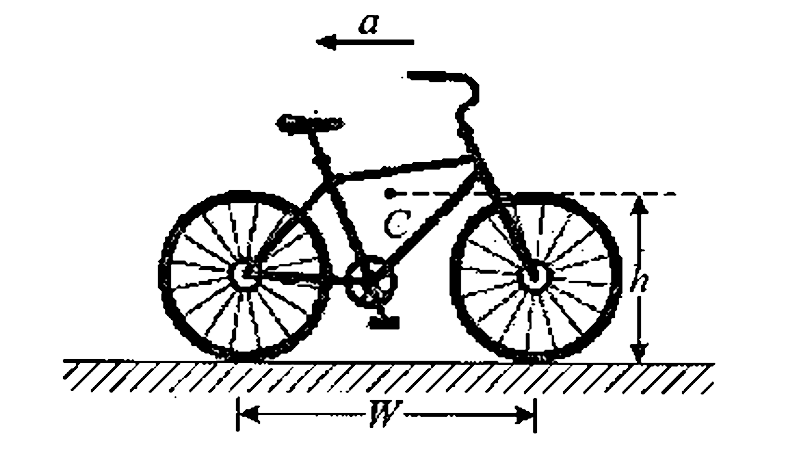
View SolutionA simplified model of a bicycle of mass M has two tires that each comes into contact with the ground at a point. The wheel base of this bicycle is JV, and the centre of mass C of the bicycle is located mid way between the tires and a height h above the ground.The bicycleis moving to the right,but slowing down at a constant acceleration a. Air resistance may be ignored. Assuming that the coefficient of sliding friction between each tyre and the ground is μ and that both tyres are skidding (sliding without rotating). Express your answer in terms of w,h,M and g .
What is the maximum value of a so that both tyres remain in contact with the ground ?
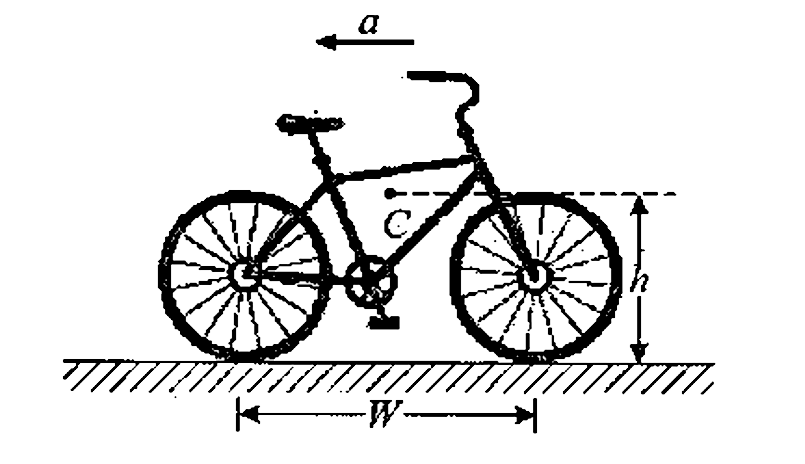
View SolutionA simplified model of a bicycle of mass M has two tires that each comes into contact with the ground at a point. The wheel base of this bicycle is JV, and the centre of mass C of the bicycle is located mid way between the tires and a height h above the ground.The bicycleis moving to the right,but slowing down at a constant acceleration a. Air resistance may be ignored. Assuming that the coefficient of sliding friction between each tyre and the ground is μ and that both tyres are skidding (sliding without rotating). Express your answer in terms of w,h,M and g .
What is the maximum value of μ so that both tires remain in contact with the ground :
View SolutionIn the shown figure, the mass in sticks to the string just after it strikes it. Then the minimum value of h, so that the lower mass bounce off the ground during 'its rebound is:
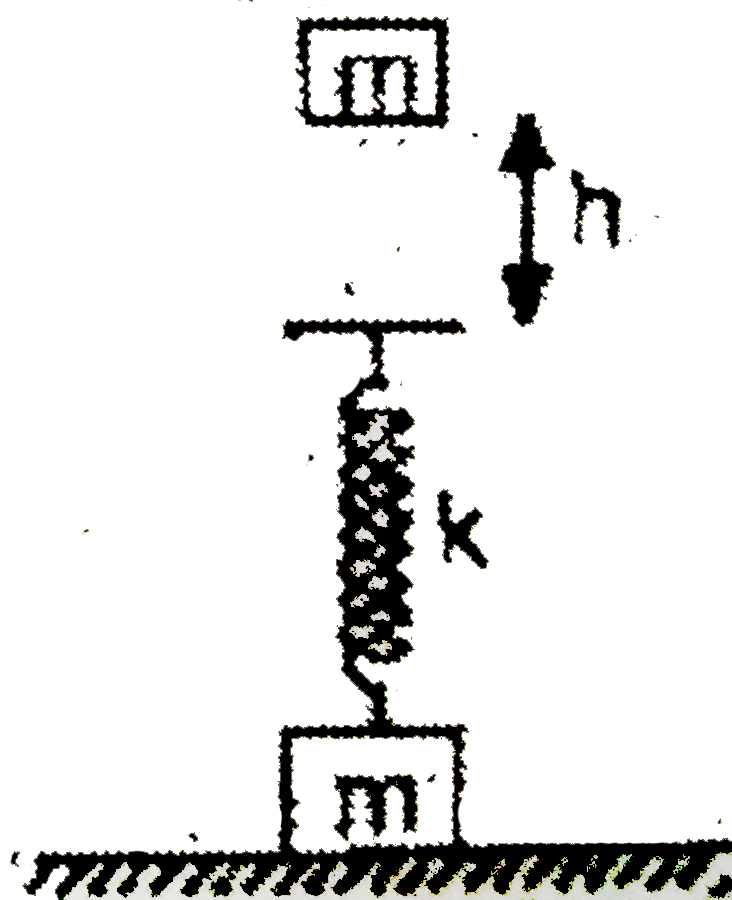
View Solution