A body of mass 100 g is attached to a hanging spring force constant is 10N/m. The body is lifted until the spring is in its unstretched state and then released. Calculate the speed of the body when it strikes the table 15cm release point .
1m/s
0.866m/s
0.225m/s
1.5m/s
The correct Answer is:B
Ei=Ef
0=12×10×(0.15)2−0.1×10×0.15
+12×0.1×v2
∴v=0.866m/s.
Topper's Solved these Questions
- WORK, ENERGY & POWERBOOK - DC PANDEYCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 1 subjective
27 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEYCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 objective
30 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEYCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 1 Assertion and Reason
12 Videos
- WAVE MOTIONBOOK - DC PANDEYCHAPTER - WAVE MOTIONEXERCISE - Integer Type Question
11 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEYCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY
33 Videos
Similar Questions
Knowledge Check
If a body of mass 0.98 kg is made to oscillate on a spring of force constant 4.84 N/m the angular frequency of the body is
A1.22 rad/sB2.22 rad/sC3.22 rad/sD4.22 rad/s
A block of mass m is attached to two unstretched springs of spring constant k, each as shown. The block is displaced towards right through a distance x and is released The speed of the block as it passes through the mean position will beAx√m2kBx√2kmCxmkDx2kmA body of mass of 4 kg is mounted on four vertical springs each having a spring constant of 400 N/m. The period with which the body vibrates vertically is
A3.14 sB0.314 sC0.628 sD0.157 s
A block of mass 'm' is attached to the light spring of force constant K and released when it is in its natural length. Find amplitude of subsequent oscillations.
View SolutionA block of mass m = 2 kg is attached to two unstretched spring of force constant k1=100N/m and k2=125N/m
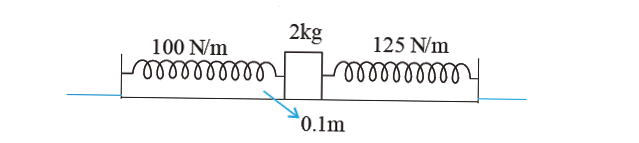
The block is displaced towards left through a distance of 10 cm and released. Find the speed of the block as it passes through the mean position.
View SolutionA body of mass 0.10kg is attached to vertical massless spring with force constant 4.0×103N/m. The body is displaced 10.0cm from its equilibrium position and released. How much time elapses as the body moves from a point 8.0cm on one side of the equilibrium position to a point 6.0cm on the same side of the equilibrium position ?
View SolutionA block of mass 1 kg is suspended from a spring of constant 100 N/m. initially the spring is unstretched. The block is then released. What is the acceleration (in m/s2) of the block when its velocity is 0.6 m/s in the downwards direction ?
View SolutionA body of mass 1 kg is made to oscillate on a spring of force constant 16 N/m. Calculate (a) Angular frequncy , (b) Frequency of vibrations.
View Solution