In figure two identical particals each of mass m are tied together with an inextensible string. This is pulled at its centre wwith a constant force F. If the whole system lines on a smooth horizontal plane, then the aceleration of each partical towards each other is
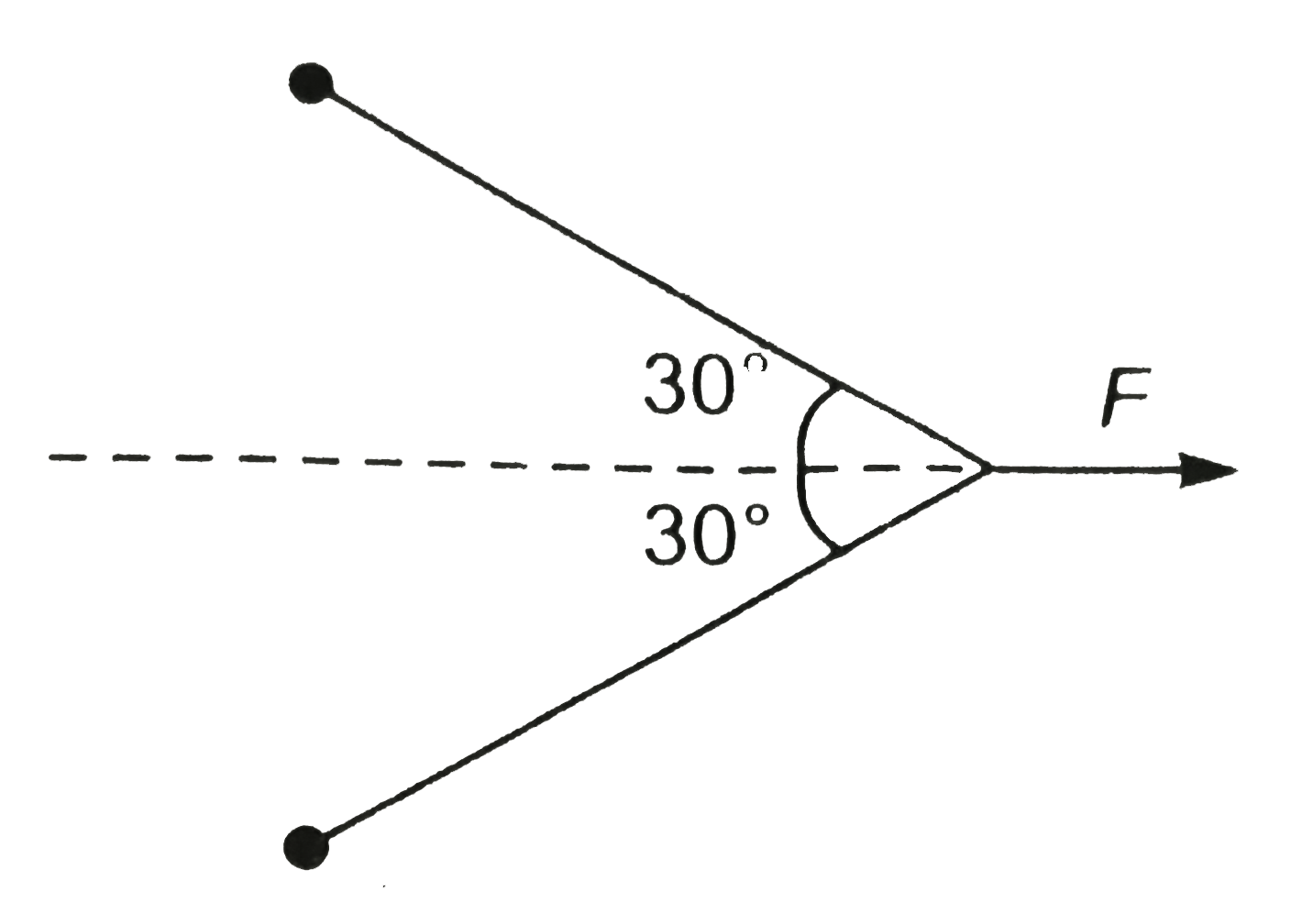
√32Fm
12√3Fm
2√3Fm
√3Fm
The correct Answer is:B
At point P.
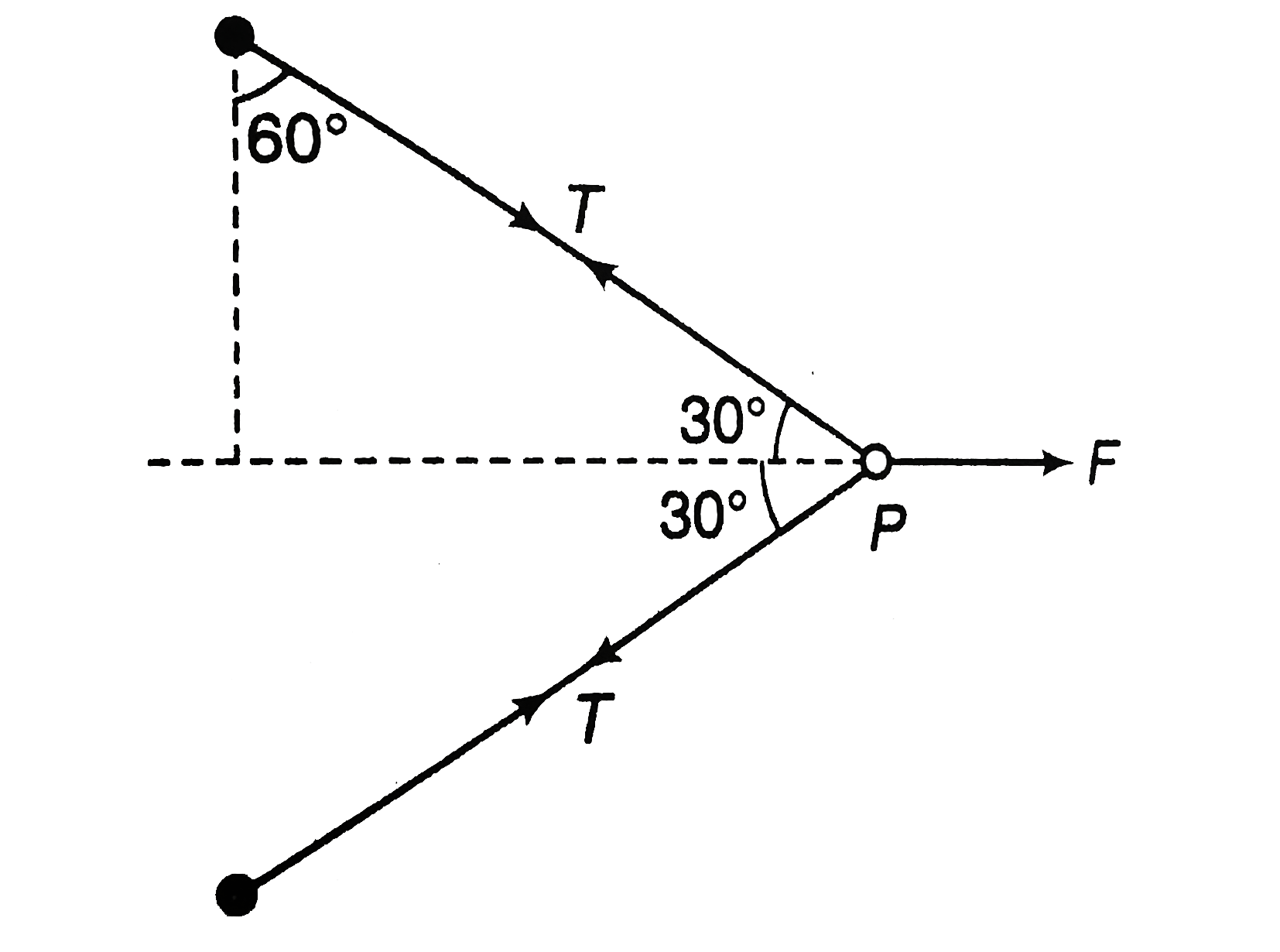
F=2Tcos30∘
T=F√3
Acceleration of partical towards each other
=component of towards each other particalm
=Tcos60∘m=(F/√3)(1/2)m=F2√3m
Topper's Solved these Questions
- LAWS OF MOTIONBook:DC PANDEYChapter:LAWS OF MOTIONExercise:Objective Question
Explore 32 Videos
- LAWS OF MOTIONBook:DC PANDEYChapter:LAWS OF MOTIONExercise:Comprehension
Explore 9 Videos
- LAWS OF MOTIONBook:DC PANDEYChapter:LAWS OF MOTIONExercise:Exercise 8.5
Explore 2 Videos
- KINEMATICS 1Book:DC PANDEYChapter:KINEMATICS 1Exercise:INTEGER_TYPE
Explore 15 Videos
- LAWS OF THERMODYNAMICSBook:DC PANDEYChapter:LAWS OF THERMODYNAMICSExercise:Level 2 Subjective
Explore 18 Videos
Similar Questions
Two blocks o equal mass m are tied to each other through light string. One of the blocks is pulled along the line joining them with a constnt force F. Find the tension in the string joining the blocks.
View SolutionTwo particles each of mass m are connected by a light inextensible string and a particle of mass M is attached to the midpoint of the string. The system is at rest on a smooth horizontal table with string just taut and in a straight line. The particle M is given a velocity v along the table perpendicular to the string. Prove that when the two particles are about to collide :
(i) The velocity of M is Mv(M+2m)
(ii) The speed of each of the other particles is (√2M(M+m)(M+2m))v.
View Solution
Knowledge Check
Two identical particles move towards each other with velocity 2v and v, respectively. The velocity of the centre of mass is:
AvBv/3Cv/2DzeroTwo identical particles move towards each other with velocity 2v and v respectively. The velocity of centre of mass is
AVBV/3CV/2DZeroTwo identical particles move towards each other with velocity 2v and v respectively. The velocity of centre of mass is
AvBv3Cv2Dzero.
Two particles each of mass m are connected by a light string of length 2L as shown in the figure. A constant force F is applied continuoulsly at the mid−point of the string at right−angle to intial position of the string. Find the acceleration of each particle and the acceleration of approach between the particles when separation between them is 2x
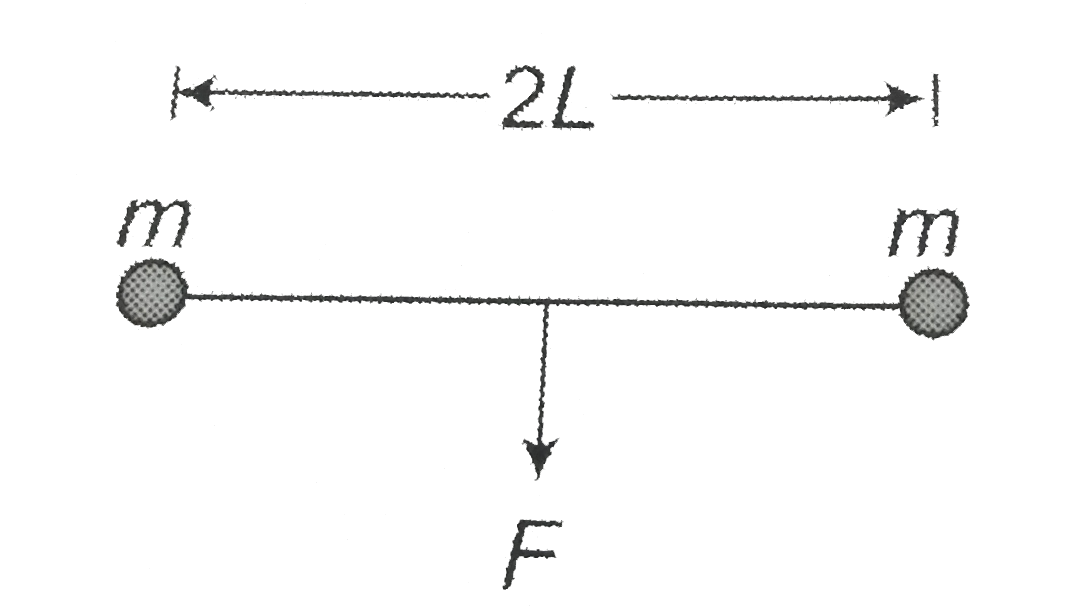
View SolutionTwo particles each of mass m are connected by a light string of length 2L as shown in the figure. A constant force F is applied continuoulsly at the mid−point of the string at right−angle to intial position of the string. Find the acceleration of each particle and the acceleration of approach between the particles when separation between them is 2x

View SolutionThree point masses each of mass m are joined together using a string to form an equilateral triangle of side a. The system is placed on a smooth horizontal surface and rotated with a constant angular velcoity ω about a vertical axis passing through the centroid Then the tension in each string is .
View SolutionTwo identical circular plates each of mass M and radius R are attached to each other with their planes ⊥r to each other. The moment of inertia of system about an axis passing through their centres and the point of contact is
View SolutionTwo identical small bodies each of mass m and charge q are suspended from two strings each of length l from a fixed point. This whole system is taken into an orbiting artificial satellite, then find the tensio in strings
View Solution