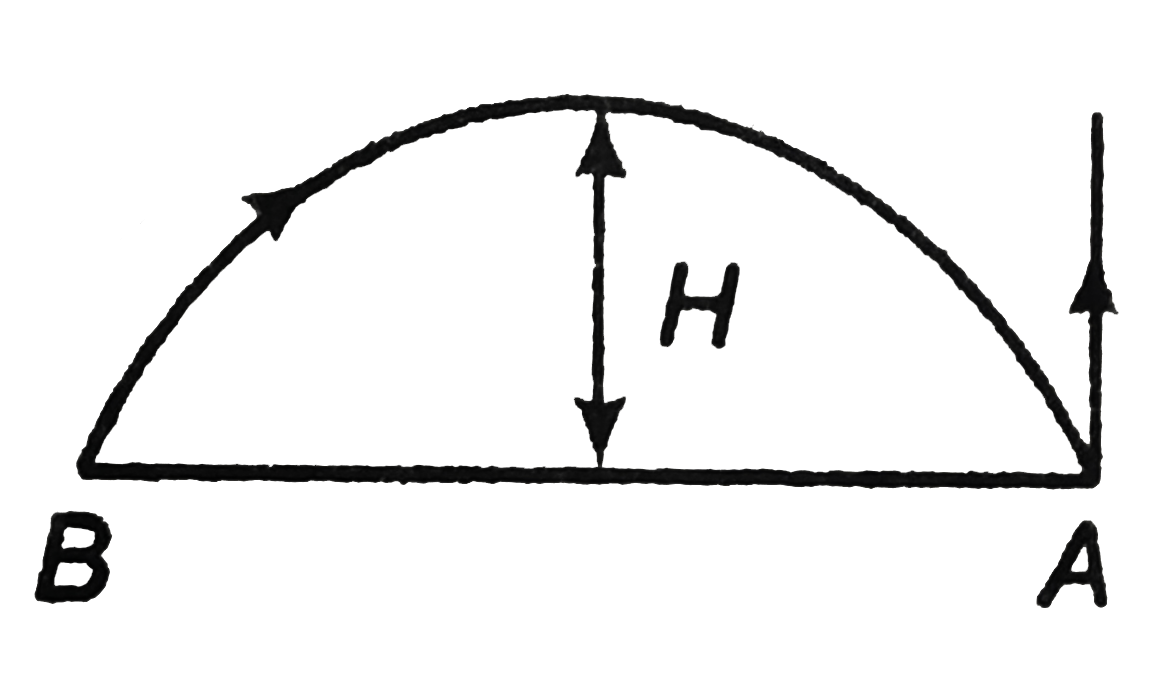
Assertion : Particle A is projected upwards. Simultaneously particle B is projected as projectile as shown. Particle A returns to ground in 4s. At the same time particle B collides with A. Maximum height H attained by B would be 20 m. (g=10ms−2) .
Reason : Speed of projectile of both the particles should be same under the given condition.
 .
.
(a)If both Assertion and Reason are true and the Reason is correct explanation of the Assertion.
(b)If both Assertion and Reason are true and the Reason is not the correct explanation of the Assertion.
(c) If Assertion is true, but the Reason is false.
(d) If Assertion is false, but the Reason is true.
The correct Answer is:C
T=2usinθg=41
∴(usinθ)=20m/s
∴H=u2sin2θ2g=20220=20m .
Topper's Solved these Questions
- PROJECTILE MOTIONBook:DC PANDEYChapter:PROJECTILE MOTIONExercise:Level - 1 Single Correct
Explore 16 Videos
- PROJECTILE MOTIONBook:DC PANDEYChapter:PROJECTILE MOTIONExercise:Level - 1 Subjective
Explore 21 Videos
- PROJECTILE MOTIONBook:DC PANDEYChapter:PROJECTILE MOTIONExercise:Exercise 7.3
Explore 6 Videos
- MOTION IN A PLANEBook:DC PANDEYChapter:MOTION IN A PLANEExercise:(C )Medical entrances gallery
Explore 32 Videos
- PROPERTIES OF MATTERBook:DC PANDEYChapter:PROPERTIES OF MATTERExercise:Integer
Explore 8 Videos
Similar Questions
A particle is projected along an inclined plane as shown in figure. What is the speed of the particle when it collides at point A ? (g=10m/s)

View SolutionA particle A is projected verically upwards. Another indentical particle B is projected at an angle of 45∘. Both reach the same height. The ratio of the initial kinetic energy of A to that of B is −
View Solution
Knowledge Check
A particle is projected from ground with velocity 3ˆi+4ˆi m/s. Find range of the projectile :-
A1.2mB3.6mC2.4mD10mA particle is projected with a speed u at an angle θ to the horizontal. Find the radius of curvature.
At the point where the particle is at a highest half of the maximum height H attained by it.A2u2(1+cos2θ)3/2g2√2cosθBu2(1+cos2θ)3/2g2√2cosθCu2(1−sin2θ)3/2g2√2cosθDu2(1−tan2θ)3/2g2√2cosθA particle is thrown vertically upwards. If its velocity is half of the maximum height is 20m/s, then maximum height attained by it is
A25 mB30 mC35 mD40 m
Particle is projected from the ground at a certain angle with horizontal . If particle takes time T to hit the ground again , then maximum height of the projectile is
View SolutionTwo particles are projected with speed 4m/s and 3m/s simultaneously from same point as shown in the figure. Then:

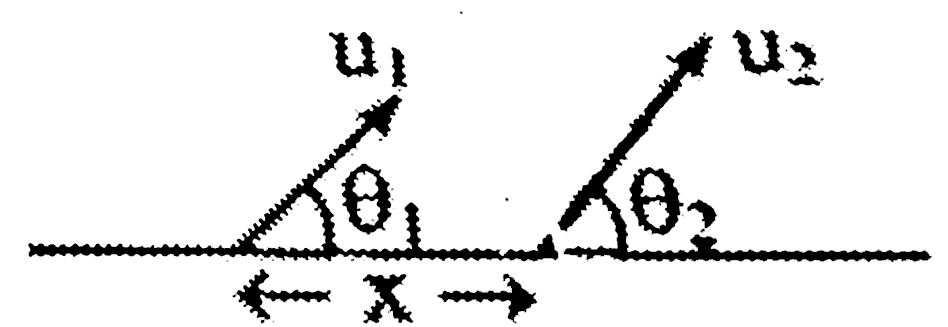
View SolutionTwo particles are projected simultaneously from the level ground as shown figure. They may collide after a time :
View SolutionAssertion Particle-1 is dropped from a tower and particle-2 is projected horizontal from the same tower. Then both the particles reach the ground simultaneously.
Reason Both are particles strike the ground with different speeds.
View SolutionAssertion: Two particles of different mass, projected with same velocity at same angles. The maximum height attained by both the particle will be same.
Reason: The maximum height of projetile is independent of particle mass.
View Solution

