A particle is moving in x-y p1ane.At time t=0, particle is at (1m,2m) and has velocity (4ˆi+6ˆj)m/s. At t=4s, particle reaches at (6m,4m) and has velocity (2ˆi+10ˆj)m/s. In the given time interval, find
(a) average velocity,
(b) average acceleration and
(c) from the given data, can you find average speed?
The correct Answer is:A, B, C
(a) vav=st=rf−rit
=(6ˆi+4ˆj)−(4ˆi+6ˆJ)4
=(1.25ˆi+0.5ˆj)m/s
(b) aav=Δvt=vf−vit
=(2ˆi+10ˆj)−(4ˆi+6ˆj)4
=(−0.5ˆi+ˆj)m/s2
(c) We cannot calculate the distance travelled from
the given data.
Topper's Solved these Questions
- KINEMATICSBook:DC PANDEYChapter:KINEMATICSExercise:More Than One Correct
Explore 6 Videos
- KINEMATICSBook:DC PANDEYChapter:KINEMATICSExercise:Comprehension
Explore 7 Videos
- KINEMATICSBook:DC PANDEYChapter:KINEMATICSExercise:Objective
Explore 45 Videos
- GRAVITATIONBook:DC PANDEYChapter:GRAVITATIONExercise:(C) Chapter Exercises
Explore 45 Videos
- KINEMATICS 1Book:DC PANDEYChapter:KINEMATICS 1Exercise:INTEGER_TYPE
Explore 15 Videos
Similar Questions
A particle is moving with velocity ˆi+2ˆj+3ˆk)m/s plane mirror exists in the x-y plane.The mirror has a velocity (ˆi+2ˆj)m/s] of the image (in m/s)
View SolutionAn a particle is moving in a magnetic field of (3ˆi+2ˆj) tesla with a velocity of 5×105ˆi m/s. The magnetic force acting on the particle will be-
View Solution
Knowledge Check
At time t=0, a particle is at (−1m,2m) and at t=2s it is at (−4m,6m). From this we can conclude that in the given time interval.
Aparticle may be accelerateBparticle may be acceleratedCaverage speed of the particle is 2.5m/sDaverage velocity of the particle is 2.5m/sA particle is moving in x-y plane. At an instant, it has velocity (4ˆi+4ˆj)m/s and acceleration (3ˆi+5ˆj)m/s2 At that instant, the radius of curvature of its path will be :
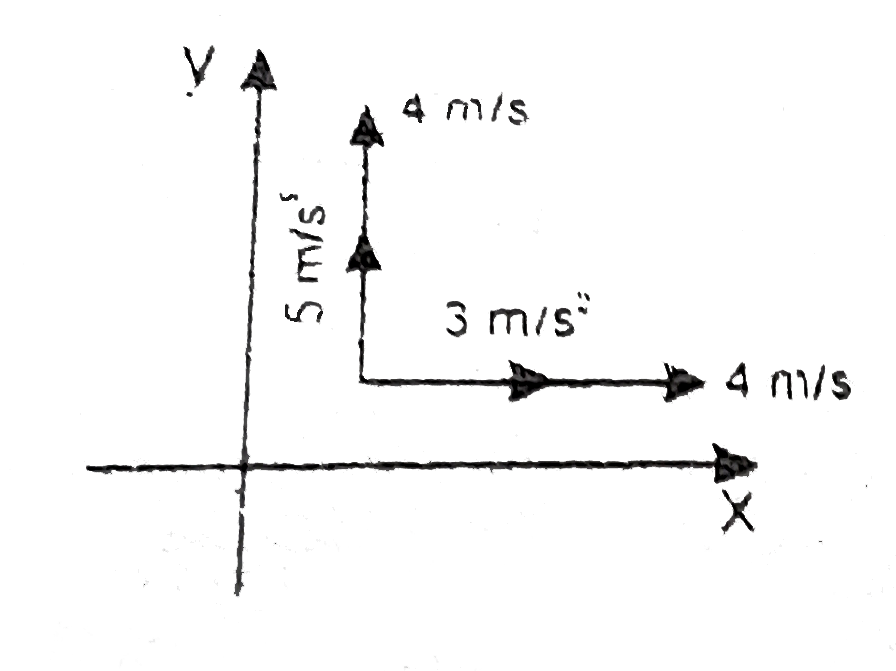 A16√2mB15 mC18 mDNon of these
A16√2mB15 mC18 mDNon of theseVelocity of a particle at some instant is v=(3ˆi+4ˆj+5ˆk)m/s. Find speed of the particle at this instant.
A12B7C-12D5√2
A particle is moving with initial velocity 1m/s and acceleration a=(4t+3)ms2. Find velocity of particle at t=2sec.
View SolutionA particle of mass 2√5Kg is having velocity →v=(2ˆi+ˆj)ms" and acceleration →a=(ˆj−ˆi)ms2" at some instant of time. At same instant find component of net force (in N) parallel to velocity.
View SolutionA particle of mass 5 kg moving in the x-y plane has its potential energy given by U=(−7x+24y)J where x and y are in meter. The particle is initially at origin and has a velocity →i=(14ˆi+4.2ˆj)m/s
View SolutionA particle has initial velocity (3ˆi+4ˆj) and has acceleration (0.1ˆi+0.3ˆj). Its speed after 10s is.
View SolutionA particle of mass 2kg is projected with a velocity (6ˆi+8ˆj) m/s. Find the magnitude of change in momentum (in kg m/s) when it just touches ground again.
View Solution

