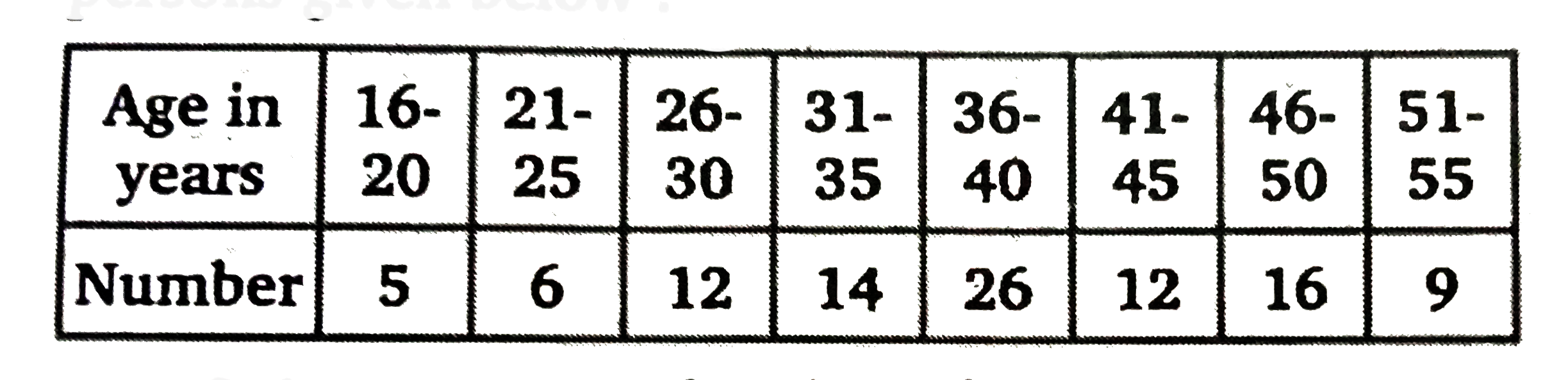Calculate the mean deviation about median age for the age distribution of 100 persons given below:Age 16-20 21-25 26-30 31-35 36-40 41-45 46-50 51-55Number 5 6 12 14 26 12 16 9
To calculate the mean deviation about the median age for the given age distribution of 100 persons, we will follow these steps:
Step 1: Convert Age Groups to Continuous Intervals
The age groups provided are not continuous, so we will convert them to continuous intervals by adjusting the lower and upper limits.
- For 16-20, the continuous interval is 15.5 to 20.5
- For 21-25, the continuous interval is 20.5 to 25.5
- For 26-30, the continuous interval is 25.5 to 30.5
- For 31-35, the continuous interval is 30.5 to 35.5
- For 36-40, the continuous interval is 35.5 to 40.5
- For 41-45, the continuous interval is 40.5 to 45.5
- For 46-50, the continuous interval is 45.5 to 50.5
- For 51-55, the continuous interval is 50.5 to 55.5
Step 2: Create a Frequency Table
Now we will create a frequency table with the continuous intervals and their corresponding frequencies:
| Age Interval | Midpoint (x_i) | Frequency (f_i) |
|--------------|----------------|-----------------|
| 15.5 - 20.5 | 18 | 5 |
| 20.5 - 25.5 | 23 | 6 |
| 25.5 - 30.5 | 28 | 12 |
| 30.5 - 35.5 | 33 | 14 |
| 35.5 - 40.5 | 38 | 26 |
| 40.5 - 45.5 | 43 | 12 |
| 45.5 - 50.5 | 48 | 16 |
| 50.5 - 55.5 | 53 | 9 |
Step 3: Calculate Cumulative Frequency
Next, we calculate the cumulative frequency:
| Age Interval | Frequency (f_i) | Cumulative Frequency |
|--------------|-----------------|----------------------|
| 15.5 - 20.5 | 5 | 5 |
| 20.5 - 25.5 | 6 | 11 |
| 25.5 - 30.5 | 12 | 23 |
| 30.5 - 35.5 | 14 | 37 |
| 35.5 - 40.5 | 26 | 63 |
| 40.5 - 45.5 | 12 | 75 |
| 45.5 - 50.5 | 16 | 91 |
| 50.5 - 55.5 | 9 | 100 |
Step 4: Determine the Median
The median is the value at the N2th position, where N is the total frequency (100). Thus, we look for the 50th term.
From the cumulative frequency, we see that the 50th term falls in the interval 35.5 - 40.5.
To calculate the median:
- Lower boundary (L) = 35.5
- Cumulative frequency before the median class (cf) = 37
- Frequency of the median class (f) = 26
- Class width (h) = 5 (40.5 - 35.5)
Using the median formula:
Median=L+⎛⎝N2−cff⎞⎠×h
Median=35.5+(50−3726)×5
=35.5+(1326)×5
=35.5+2.5=38
Step 5: Calculate Mean Deviation
Now we calculate the mean deviation about the median. We need to find |xi−Median| for each midpoint and then multiply by the frequency.
| Midpoint (x_i) | Frequency (f_i) | |x_i - Median| | f_i * |x_i - Median| |
|----------------|-----------------|-----------------|-------------------|
| 18 | 5 | 20 | 100 |
| 23 | 6 | 15 | 90 |
| 28 | 12 | 10 | 120 |
| 33 | 14 | 5 | 70 |
| 38 | 26 | 0 | 0 |
| 43 | 12 | 5 | 60 |
| 48 | 16 | 10 | 160 |
| 53 | 9 | 15 | 135 |
Now we sum the last column:
Total=100+90+120+70+0+60+160+135=775
Step 6: Calculate Mean Deviation
Finally, we calculate the mean deviation:
Mean Deviation=TotalN=775100=7.75
Final Answer
The mean deviation about the median age is 7.75.
---
The age groups provided are not continuous, so we will convert them to continuous intervals by adjusting the lower and upper limits.
- For 21-25, the continuous interval is 20.5 to 25.5
- For 26-30, the continuous interval is 25.5 to 30.5
- For 31-35, the continuous interval is 30.5 to 35.5
- For 36-40, the continuous interval is 35.5 to 40.5
- For 41-45, the continuous interval is 40.5 to 45.5
- For 46-50, the continuous interval is 45.5 to 50.5
- For 51-55, the continuous interval is 50.5 to 55.5
Now we will create a frequency table with the continuous intervals and their corresponding frequencies:
|--------------|----------------|-----------------|
| 15.5 - 20.5 | 18 | 5 |
| 20.5 - 25.5 | 23 | 6 |
| 25.5 - 30.5 | 28 | 12 |
| 30.5 - 35.5 | 33 | 14 |
| 35.5 - 40.5 | 38 | 26 |
| 40.5 - 45.5 | 43 | 12 |
| 45.5 - 50.5 | 48 | 16 |
| 50.5 - 55.5 | 53 | 9 |
Next, we calculate the cumulative frequency:
|--------------|-----------------|----------------------|
| 15.5 - 20.5 | 5 | 5 |
| 20.5 - 25.5 | 6 | 11 |
| 25.5 - 30.5 | 12 | 23 |
| 30.5 - 35.5 | 14 | 37 |
| 35.5 - 40.5 | 26 | 63 |
| 40.5 - 45.5 | 12 | 75 |
| 45.5 - 50.5 | 16 | 91 |
| 50.5 - 55.5 | 9 | 100 |
The median is the value at the N2th position, where N is the total frequency (100). Thus, we look for the 50th term.
- Lower boundary (L) = 35.5
- Cumulative frequency before the median class (cf) = 37
- Frequency of the median class (f) = 26
- Class width (h) = 5 (40.5 - 35.5)
Median=L+⎛⎝N2−cff⎞⎠×h
Median=35.5+(50−3726)×5
=35.5+(1326)×5
=35.5+2.5=38
Now we calculate the mean deviation about the median. We need to find |xi−Median| for each midpoint and then multiply by the frequency.
|----------------|-----------------|-----------------|-------------------|
| 18 | 5 | 20 | 100 |
| 23 | 6 | 15 | 90 |
| 28 | 12 | 10 | 120 |
| 33 | 14 | 5 | 70 |
| 38 | 26 | 0 | 0 |
| 43 | 12 | 5 | 60 |
| 48 | 16 | 10 | 160 |
| 53 | 9 | 15 | 135 |
Total=100+90+120+70+0+60+160+135=775
Finally, we calculate the mean deviation:
Mean Deviation=TotalN=775100=7.75
The mean deviation about the median age is 7.75.
Topper's Solved these Questions
- STATISTICSBOOK - NCERTCHAPTER - STATISTICSEXERCISE - EXERCISE 15.3
5 Videos
- STATISTICSBOOK - NCERTCHAPTER - STATISTICSEXERCISE - EXERCISE 15.2
10 Videos
- STATISTICSBOOK - NCERTCHAPTER - STATISTICSEXERCISE - SOLVED EXAMPLES
18 Videos
- SETSBOOK - NCERTCHAPTER - SETSEXERCISE - EXERCISE 1.5
7 Videos
- STRAIGHT LINESBOOK - NCERTCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE 10.5
2 Videos
Similar Questions
Knowledge Check
The mean deviation about the mean for the values
18, 20, 12, 14, 19, 22, 26, 16, 19, 24 isA3.1B3.4C3.2D3.3
Calculate mean deviation from the median for the following distribution: xi: 10 15 20 25 30 35 40 45 fi: 7 3 8 5 6 8 4 9
View SolutionCalculate the mean deviation about the mean for the following frequency distribution Class interval 0−4,4−8,8−12,12−16,16−20 Frequency 4,6,8,5,2
View SolutionFind the mean deviation about the median for the data given below.
45,36,50,60,53,46,51,48,72,42.
View SolutionFind the mean deviation about the median of the following frequency distribution: Class:, 0-6, 6-12, 12-18, 18-24, 24-30 Frequency:, 8, 10, 12, 9, 5
View SolutionCalculate mean deviation from the median for the following distribution: xi: , 10, 15, 20, 25, 30, 35, 40, 45 fi: , 7, 3, 8, 5, 6, 8, 4, 9
View SolutionFind the Mean deviation (about Mean) of the following observation 2,3,5,6,9,10,12,17,20,26.
View SolutionFind the mean deviation about median for the following data
View Solution