A simple pendulum of length l has a maximum angular displacement θ. The maximum kinetic energy of the bob of mass m will be
mgl(1+cosθ)
mgl(1+cos2θ)
mgl(1−cosθ)
mgl(cosθ−1)
The correct Answer is:C
According to question, when bob is at rest, the pendulum has only potential energy
(PE) = mgl
When bob displaced by smaller angular displacement 0, the pendulum loses PE of bob and it gets converted into kinetic energy (KE). So, from conservation of energy Loss in PE = gain in KE
∴KE=mgl−mgicosθ=mgl(1−cosθ)
Topper's Solved these Questions
Similar Questions
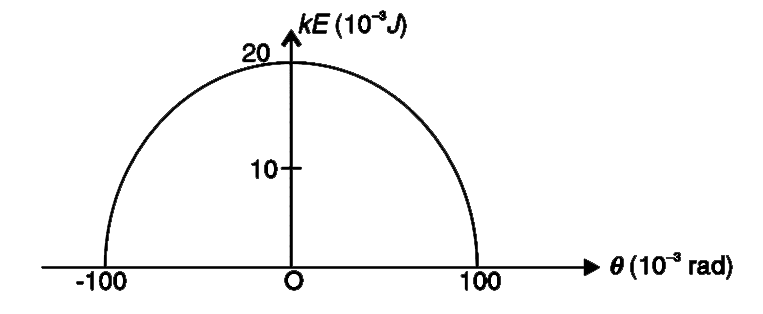
The given figure shows the variation of the kinetic energy of a simple pendulum with its angular displacement (θ) from the vertical. Mass of the pendulum bob is m = 0.2 kg. Find the time period of the pendulum. Take g=10ms−2.
View SolutionA string of length l and mass m is fixed at both ends with tension t and excited in its fundamental mode.The maximum displacement at the mid point is A Find (a) the maximum kinetic energy of the string ,9b0 the mean kinetic energy of the srting averaged over one oscillation period
hint Take sine distribution of amplitudes
View Solution
Knowledge Check
A simple pendulum of length l has maximum angular displacement θ . Then maximum kinetic energy of a bob of mass m is
A12mglB12mglcosθCmgl(1−cosθ)D12mglsinθIf a simple pendulum of length l has maximum angular displacement θ, then the maximum velocity of the bob is
A√LgB2√glsin(θ2)C√2glsinθD√2glA simple pendulum is oscillating with a maximum angular displacement of θ radian. If θ is very small, the ratio of maximum tension to the minimum tension in the string during oscillations is
A(1+θ2):(1−θ2)B(1+θ2):(1−θ22)C(1+θ2):1D(1+θ22):(1−θ2)
A simple pendulum of length l and with a bob of mass m moving alon a circular are of angle θ in a vertical plane. A sphere of mass m is placed at the end of the circular arc. What momentum will be given to the sphere by the moving bob?
View SolutionKinetic energy of the bob of a simple pendulum is maximum
View SolutionA simple pendulum having a bob of mass 100 g is oscillating with a maximum angular displacement of 3∘. The maximum restoring force acting on the bob is (take g=10ms−2)
View SolutionThe bob of a simple pendulum of length L is released at time t = 0 from a position of small angular displacement θ0 . Its linear displacement at time t is given by :
View SolutionA simple pendulum of mass 'm' , swings with maximum angular displacement of 60∘ . When its angular displacement is 30∘ ,the tension in the string is
View Solution
