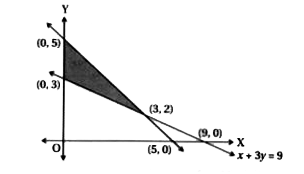
The feasible region for a LPP is shown in Fig. 12.10. Evaluate Z = 4x + y at each of the corner points of this region. Find the minimum value of Z if it exists.
Now we see that 3 is the smallest value of Z the comer point 0 3. Note that here we see that the region is unbounded therefore 3 may not be the minimum value of Z. To decide this issue we graph the inequality 4x + y < 3 and check whether the resulting open half plane has no point in common with feasible region otherwise Z has no minimum value. From the shown graph above it is clear that there is no point in common with feasible region and hence Z has minimum value 3 at 0 3.
Related Solutions
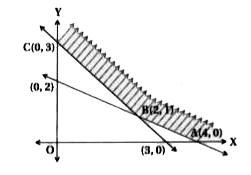
The feasible region for a LPP is shown in the following figure. Evaluate Z=4x+y at each of the corner points of the region. Find the minimum value of Z, if it exists
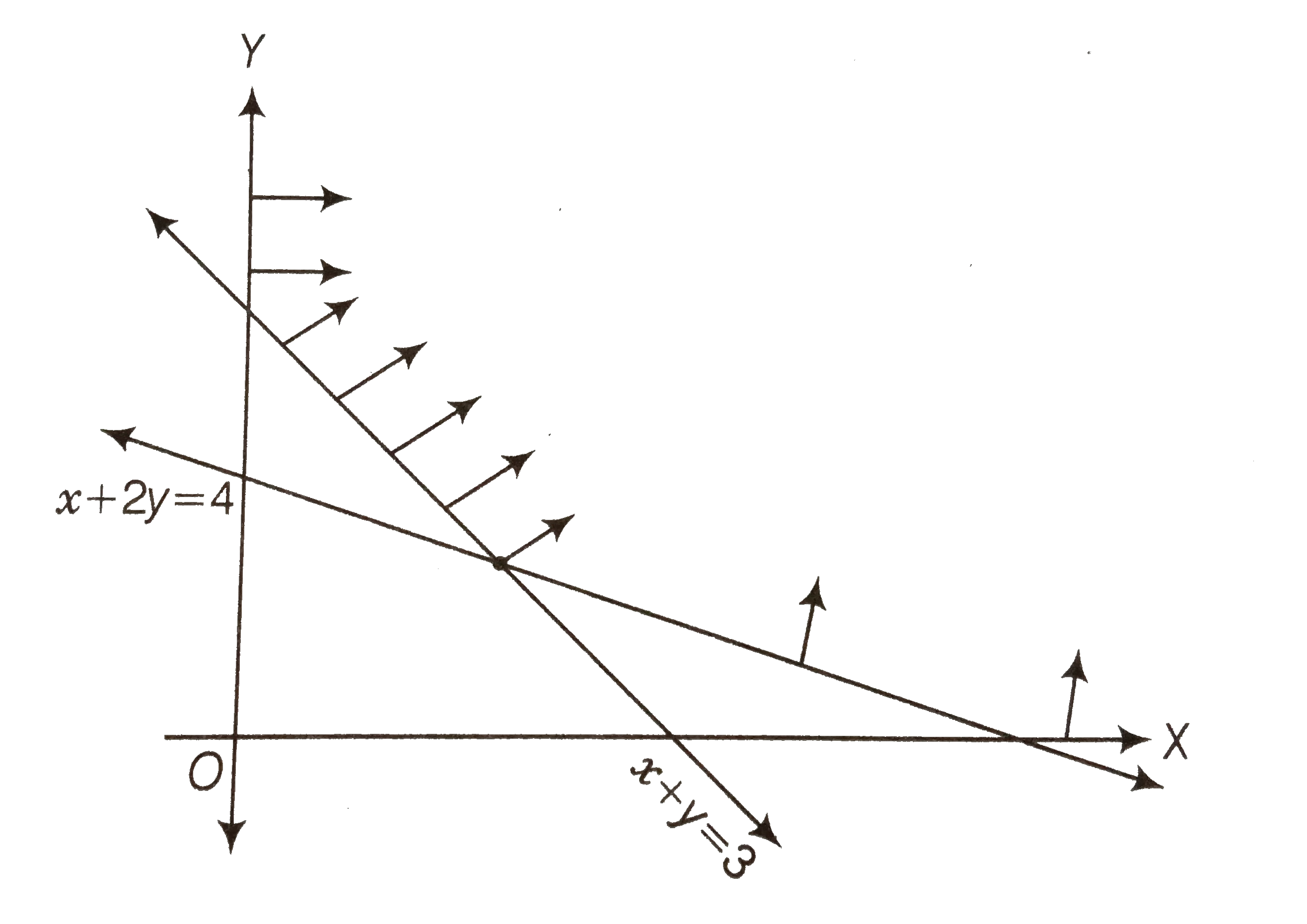
View SolutionThe feasible region for a LPP is shown in the following figure. Evaluate Z=4x+y at each of the corner points of the region. Find the minimum value of Z, if it exists

View SolutionThe feasible region for a LPP is shown in Figure. Evaluate z = 4x + y at each of the corner points at this region. Find the minimum value of z, if exists.
View Solutionकिसी LPP का सुसंगत क्षेत्र आकृति में प्रदर्शित है। इस क्षेत्र के प्रत्येक कोनीय बिंदु पर Z= 4x + y का मान निकालिए। Z का न्यूनतम मान ज्ञात कीजिए, यदि उसका अस्तित्व है।
View SolutionThe feasible region for an LPP is shown shaded in the figure 12.48 find the minimum value of Z=4x+y.
View SolutionThe feasible region of an LPP is shown in the figure. If z = 3x + 9 y , then the minimum value of z occurs at
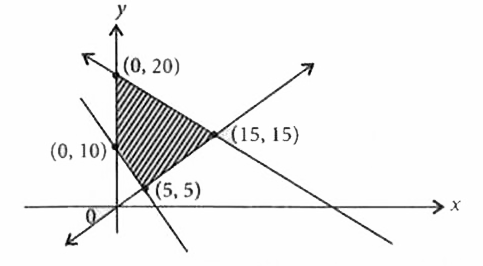
View SolutionThe feasible region for a LPP is shown in Figure. Find the minimum value of .
View SolutionThe feasible region for LPP is shown shaded in the figure . Find the minimum value of the objective function z = 11x + 7y.
View SolutionThe feasible region for an LPP is shown in following figure. Find the minimum value of
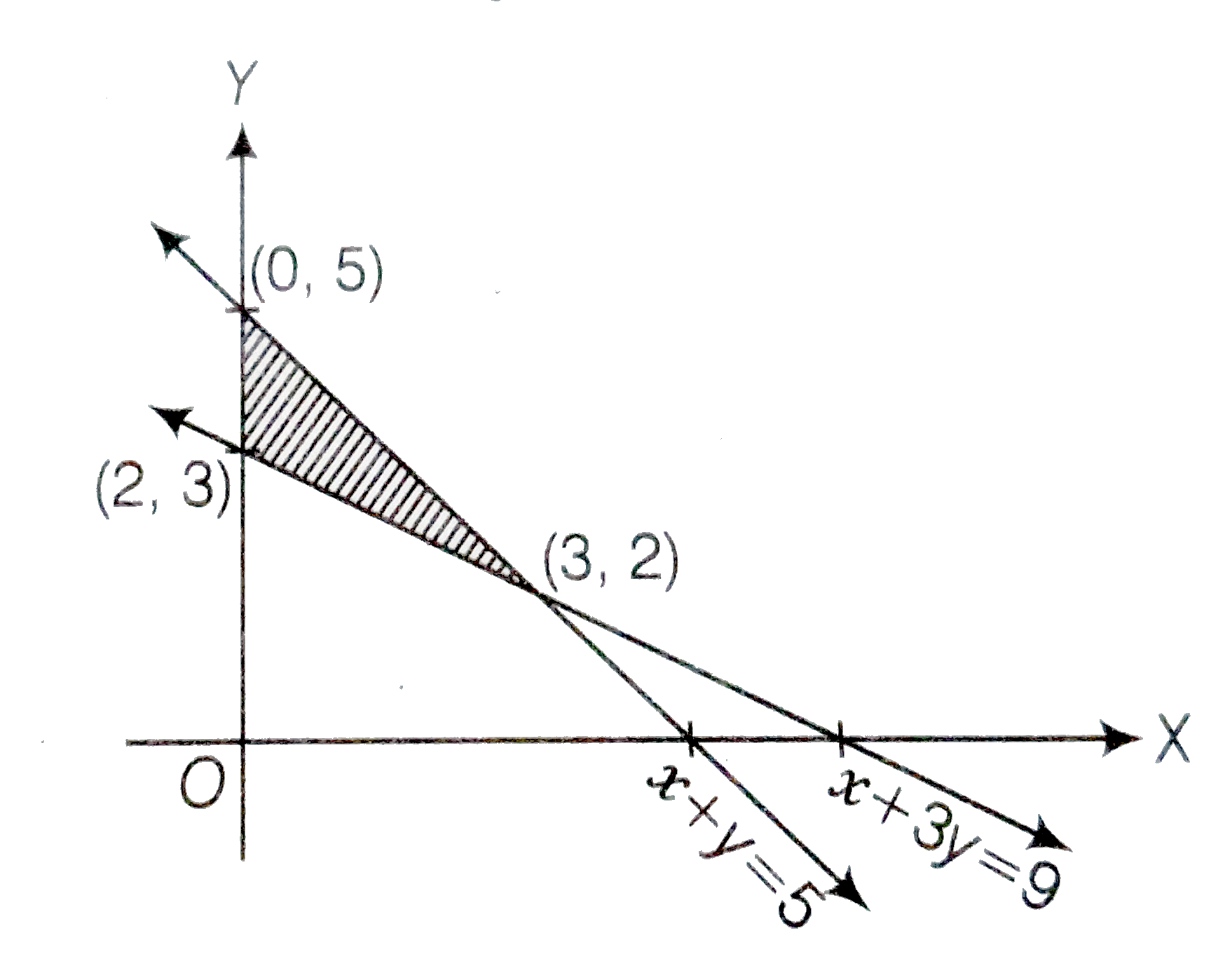
View SolutionThe feasible region for an LPP is shown in following figure. Find the minimum value of Z=11x+7y.

View SolutionConsider the following statements
I. If the feasible region of an LPP is undbounded then maximum or minimum value of the obJective function Z = ax + by may or may not exist .
II. Maximum value of the objective function Z = ax + by in an LPP always occurs at only one corner point of the feasible region.
Ill. In an LPP, the minimum value of the objective function Z = ax + by is always 0, if origin is one of the corner point of the feasible region.
IV. In an LPP, the maximum value of the objective function Z = ax + by is always finite.
Which of the following statements are true?
View SolutionIn a LPP, the minimum value of the objective function Z = ax + by is always 0, if origin is one of the corner point of the feasible region.
View SolutionThe corner points of the feasible region of a LPP are (20,0),(10,50),(0,60) and (0,0). If Z= 50x +15y, then maximum value of Z occurs at :
View SolutionThe feasible region of an LPP is shown in the figure. If ,then the minimum value of z occurs at
View SolutionThe feasible region for an LPP is show shaded in the figure 12.45 find the minimum value of the objective function Z=11x+7y.
View SolutionIn a LPP, the maximum value of the objective function Z = ax +by is always 0, if origin is one of the corner point of the feasible region.
View SolutionIn a LPP, the maximum value of the objective function Z = ax +by is always 0, if origin is one of the corner point of the feasible region.
View SolutionMaximum value of the objective function Z = ax +by in a LPP always occurs at only one corner point of the feasible region.
View SolutionMaximum value of the objective function Z = ax +by in a LPP always occurs at only one corner point of the feasible region.
View SolutionMaximum value of the objective function Z = ax + by in a LPP always occurs at only one corner point of the feasible region.
View Solution