A mass of 1 kg attached to the bottom of a spring has a certain frequency of vibration. the following mass has to be added to it in order to reduce the frequency by half.a 1 kgb 2 kgc 3 kgd 4 kg
Related Solutions
A mass of attached to the bottom of a spring has a certain frequency of vibration. The following mass has to be added to it in order to reduce the frequency by half :
View SolutionA mass of 1 kg attached to the bottom of a spring has a certain frequency of vibration. The following mass has to be added to it in order to reduce the frequency by half :
View SolutionA mass of 1 kg attached to the bottom of a spring has a certain frequency of vibration. The following mass has to be added to it in order to reduce the frequency by half :
View SolutionTwo point masses of 3.0 kg and 1.0 kg are attached to opposite ends of a horizontal spring whose spring constant is 300Nm^(-1) as shown in the figure. The natural vibration frequency of the system is of the order of :
View SolutionTwo point masses of 3.0 kg and 1.0 kg are attached to opposite ends of a horizontal spring whose spring constant is 300 N m^(-1) as shown in the figure. The natural vibration frequency of the system is of the order of :
View SolutionTwo point masses of 3.0 kg and 1.0 kg are attached to opposite ends of a horizontal spring whose spring constant is 300 N m^(-1) as shown in the figure. The natural vibration frequency of the system is of the order of :
View SolutionTwo point masses of 3 kg and 6 kg are attached to opposite ends of horizontal spring whose spring constant is 300 Nm^(-1) as shown in the figure. The natural vibration frequency of the system is approximately
View SolutionTwo point masses of 3 kg and 6 kg are attached to opposite ends of horizontal spring whose spring constant is as shown in the figure. The natural vibration frequency of the system is approximately
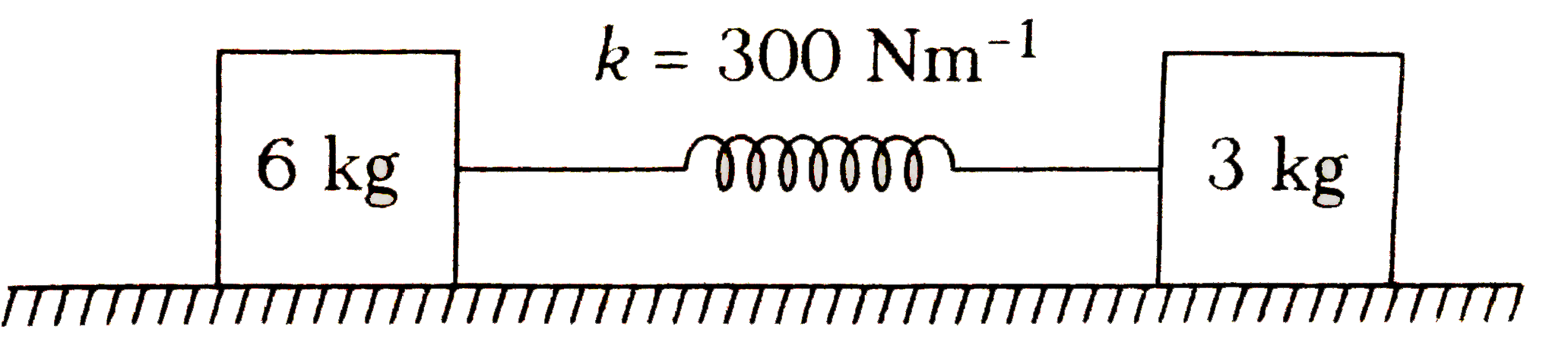
View Solutionસ્પ્રિગના નીચેના છેડે 1 kg દળ લગાડેલ છે, જેના દોલનની એક ચોક્કસ આવૃત્તિ છે. આમાં કેટલું દળ ઉમેરતાં તેની આવૃત્તિમાં અડધો ઘટાડો થાય ?
View SolutionA 1 kg block attached to a spring vibrates with a frequency of 1 Hz on a frictionless horizontal table. Two springs identical to the original spring are attached in parallel to an 8 kg block placed on the same table. So, the frequency of vibration of the 8 kg block is
View SolutionA 1 kg block attached to a spring vibrates with a frequency of 1 Hz on a frictionless horizontal table. Two springs identical to the original spring are attached in parallel to an 8 kg block placed on the same table. So, the frequency of vibration of the 8 kg block is
View SolutionA 1 kg block attached to a spring vibrates with a frequency of 1 Hz on a frictionless horizontal table. Two springs identical to the original spring are attached in parallel to an 8 kg block placed on the same table. So, the frequency of vibration of the 8 kg block is:
View SolutionA 1 kg block attached to a spring vibrates with a frequency of 1 Hz on a frictionless horizontal table. Two springs identical to the original spring are attached in parallel to an 8 kg block placed on the same table. So, the frequency of vibration of the 8 kg block is
View SolutionThe pan attached to a spring balance has a mass of 1 kg. A weight of kg when placed on the pan stretches the spring by 10 cm. What is the frequency with which the empty pan will oscillate ?
View SolutionA mass m attached to a spring A has a frequency of 3 Hz and a spring B has a frequency of 4 Hz.When both spring are connected as shown in the figure, Find the frequency (in Hz)of oscillation.
View SolutionA horizontal spring of two point masses of 3.0 kg and 1.0 kg whose spring constant 300 N m^(-1) are connected at opposite ends, as shown in the figure. The order of the fundamental vibrational frequency of the system is:
View SolutionA body of mass 4 kg is made to oscillate on a spring of force constant 10 N/m. Calculate (i) angular frequency (2) frequency of vibration and (3) time period of vibration.
View SolutionA body of mass 2 kg is made to oscillate using a spring of force constant 8Nm^(-1) find (i) angular frequency (ii) frequency of vibration (iii) time period of vibration.
View SolutionA body of mass 16 kg is made to oscillate on a spring of force constant 100 N kg^(-1) . Deduce the angular frequency.
View SolutionA body of mass 1 kg is made to oscillate in turns on springs of force constant 16 N/kg. Deduce the angular frequency.
View Solution