One end of an ideal spring is fixed to a wall at origin O and axis of spring is parallel to x-axis. A block of mass m = 1 kg is attached to free end of the spring and it is performing SHM. Equation of position of the block in co-ordinate system shown in figure is x = 10 + 3 sin10t. Here t is in second and x in cm. Another block of mass M = 3 kg moving towards the origin with velocity 30 cm/s collides with the block performing SHM at t = 0 and gets stuck to it. Calculate :a new amplitude of oscillations b new equation for position of the combined body c loss of energy during collision. Neglect friction.
At t = 0 block of mass is at mean position x = 10 cm and moving towards positive x-direction with velocity Aω or 30 cm/s.From conservation of linear momentum Substituting the values we havev = 15 cm/s or 0.15 m/sfrom conservation of mechanical energy
Related Solutions
One end of an ideal spring is fixed to a wall at origin 'O' and axis of spring is parallel to x-axis. A block of mass m = kg is attached to free end of the spring and it is performing SHM. Equation of position of the block in co-ordinate system shown in figure is x = 10+35 m (10 t) Here 't' is in second and 'x' in cm. Another block of mass M = 3kg moving towards the origin with velocity 30 cm/sec collides with the block per forming SHM at t= O and gets stick to it calculate (a) New amplitude of oscillations, (b) New equation for position of the combined body (c) Loss of energy during collision [Neglect friction]
View SolutionOne end of an ideal spring is fixed to a wall at origin and axis of spring is parallel to x-axis. A block of mass is attached to free end of the spring and it is performing SHM. Equation of position of the block in co-ordinate system shown in figure is . Here, t is in second and in . Another block of mass , moving towards the origin with velocity collides with the block performing SHM at and gets stuck to it. Calculate

(a) new amplitude of oscillations,
(b) neweqution for position of the combined body,
( c) loss of energy during collision. Neglect friction.
View SolutionOne end of an ideal spring is fixed to a wall at origin and axis of spring is parallel to x-axis. A block of mass is attached to free end of the spring and it is performing SHM. Equation of position of the block in co-ordinate system shown in figure is . Here, t is in second and in . Another block of mass , moving towards the origin with velocity collides with the block performing SHM at and gets stuck to it. Calculate
(a) new amplitude of oscillations,
(b) new equation for position of the combined body,
( c) loss of energy during collision. Neglect friction.
View SolutionOne end of an ideal spring is fixed to a wall at origin O and axis of spring is parallel to x-axis. A block of mass m = 1kg is attached to free end of the spring and it is performing SHM. Equation of position of the block in co-ordinate system shown in figure is x = 10 + 3 sin (10t) . Here, t is in second and x in cm . Another block of mass M = 3kg , moving towards the origin with velocity 30 cm//s collides with the block performing SHM at t = 0 and gets stuck to it. Calculate (a) new amplitude of oscillations, (b) neweqution for position of the combined body, ( c) loss of energy during collision. Neglect friction.
View SolutionA block of mass 2.0 kg is moving on a frictionless horizontal surface with a velocity of 1.0 m/s figure towards abnother block of equal mass kept at rest. The spring constant of the spring fixed at one end is 100 The spring constant of the spring fixed at one end is 10 N/m. Find the maximum compression of the spring.
View SolutionA block of mass m is attached to one end of a mass less spring of spring constant k. the other end of spring is fixed to a wall the block can move on a horizontal rough surface. The coefficient of friction between the block and the surface is mu then the compession of the spring for which maximum extension of the spring becomes half of maximum compression is .
View SolutionA block of mass m is attached to one end of a mass less spring of spring constant k. the other end of spring is fixed to a wall the block can move on a horizontal rough surface. The coefficient of friction between the block and the surface is mu then the compession of the spring for which maximum extension of the spring becomes half of maximum compression is .
View SolutionA spring of force constant K rests on a smooth floor, with one end fixed to a wall. A block of mass m hits the free end of the spring with velocity v. The maximum force exerted by the spring on the wall is
View SolutionCalculate the period of oscillation of a block of mass 0.5 kg attached to a spring (spring constant 100Nm^(-1) ) at one end.
View SolutionA spring has natural length and spring constant . A block of mass is attached at one end of the spring and other end of the spring is attached to a ceiling. The block is relesed from the position, where the spring has length .
View SolutionA spring has natural length and spring constant . A block of mass is attached at one end of the spring and other end of the spring is attached to a ceiling. The block is relesed from the position, where the spring has length .
View SolutionIn the figure shown a block of masss is atteched at ends of two spring The other ends of the spring are fixed The mass is released in the vertical plane when the spring are released The velocity of the block is maximum when
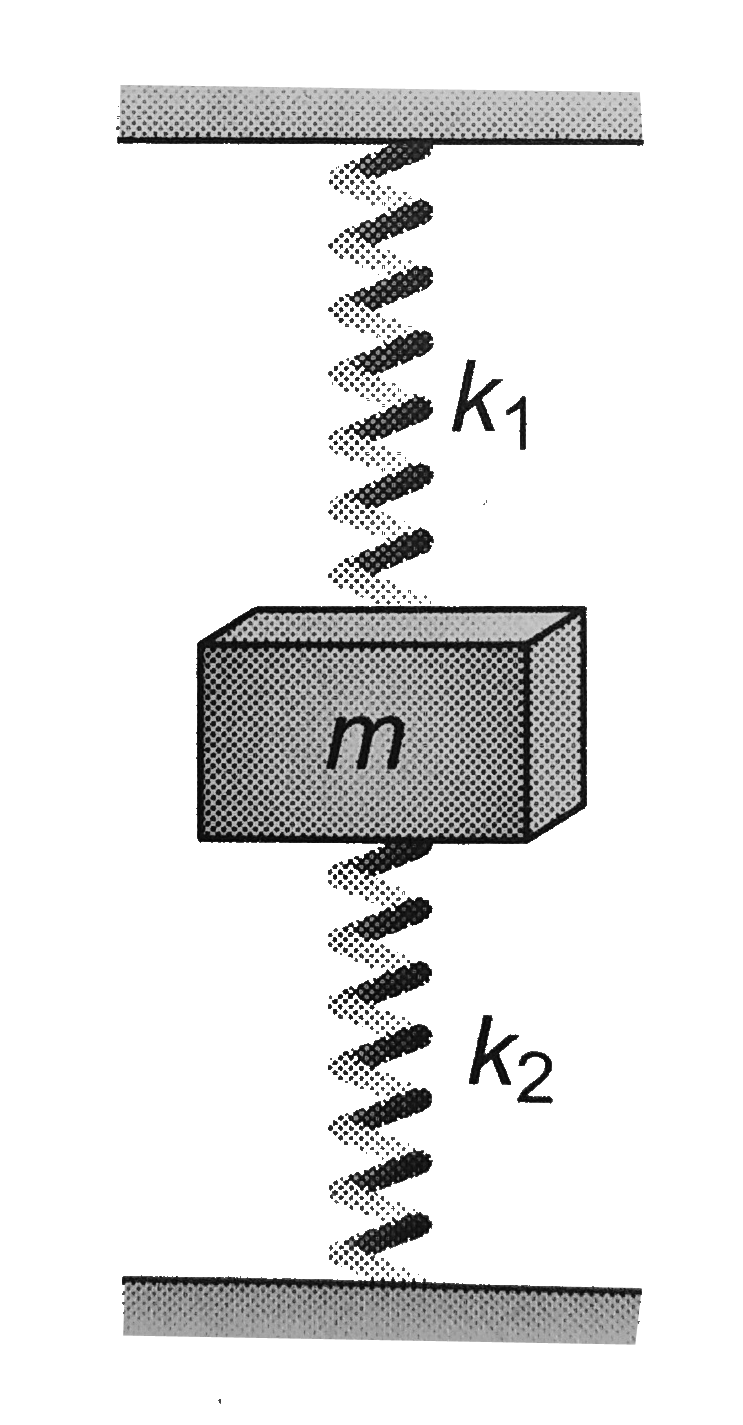
View SolutionA block of mass m = 25 kg on a smooth horizontal surface with a velocity vec v = 3 ms^(-1) meets the spring of spring constant k = 100 N//m fixed at one end as shown in figure. The maximum compression of the spring and velocity of block as it returns to the original position respectively are. .
View SolutionA block of mass m is dropped onto a spring of constant k from a height h . The second end of the spring is attached to a second block of mass M as shown in figure. Find the minimum value of h so that the block M bounces off the ground. If the block of mass m sticks to the spring immediately after it comes into contact with it.
View SolutionA block of mass m is dropped onto a spring of constant k from a height h . The second end of the spring is attached to a second block of mass M as shown in figure. Find the minimum value of h so that the block M bounces off the ground. If the block of mass m sticks to the spring immediately after it comes into contact with it.
View SolutionA block of mass lies on a horizontal frictionless surface and is attached to one end of a horizontal spring (with spring constant ) whose other end is fixed . The block is intinally at rest at the position where the spring is unstretched . When a constant horizontal force in the positive direction of the axis is applied to it, a plot of the resulting kinetic energy of the block versus its position is shown in figure. What is the magnitude of ?
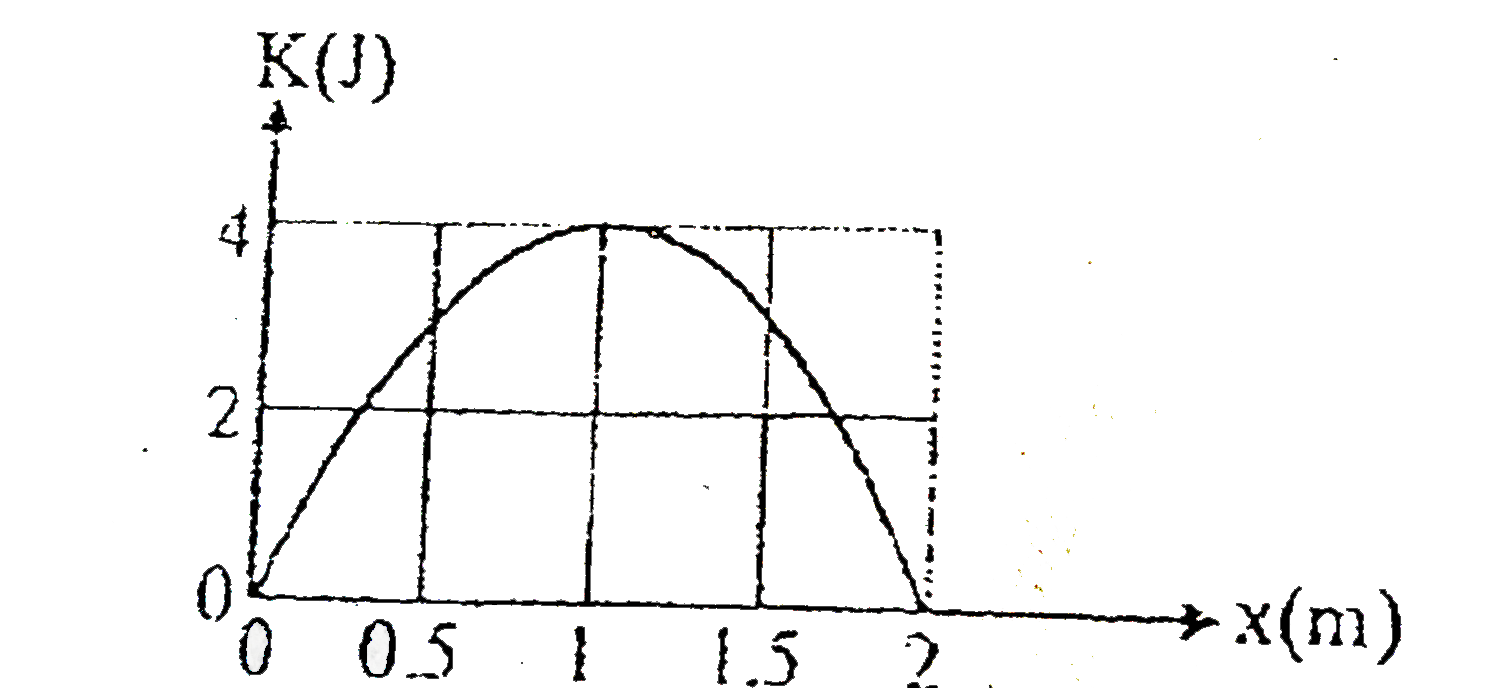
View SolutionA block of mass lies on a horizontal frictionless surface and is attached to one end of a horizontal spring (with spring constant ) whose other end is fixed . The block is intinally at rest at the position where the spring is unstretched . When a costant horizontal force in the positive direction of the axis is applied to it, a plot of the resulting kinetic energy of the block verus its position is shown in figure. What is the magnitude of
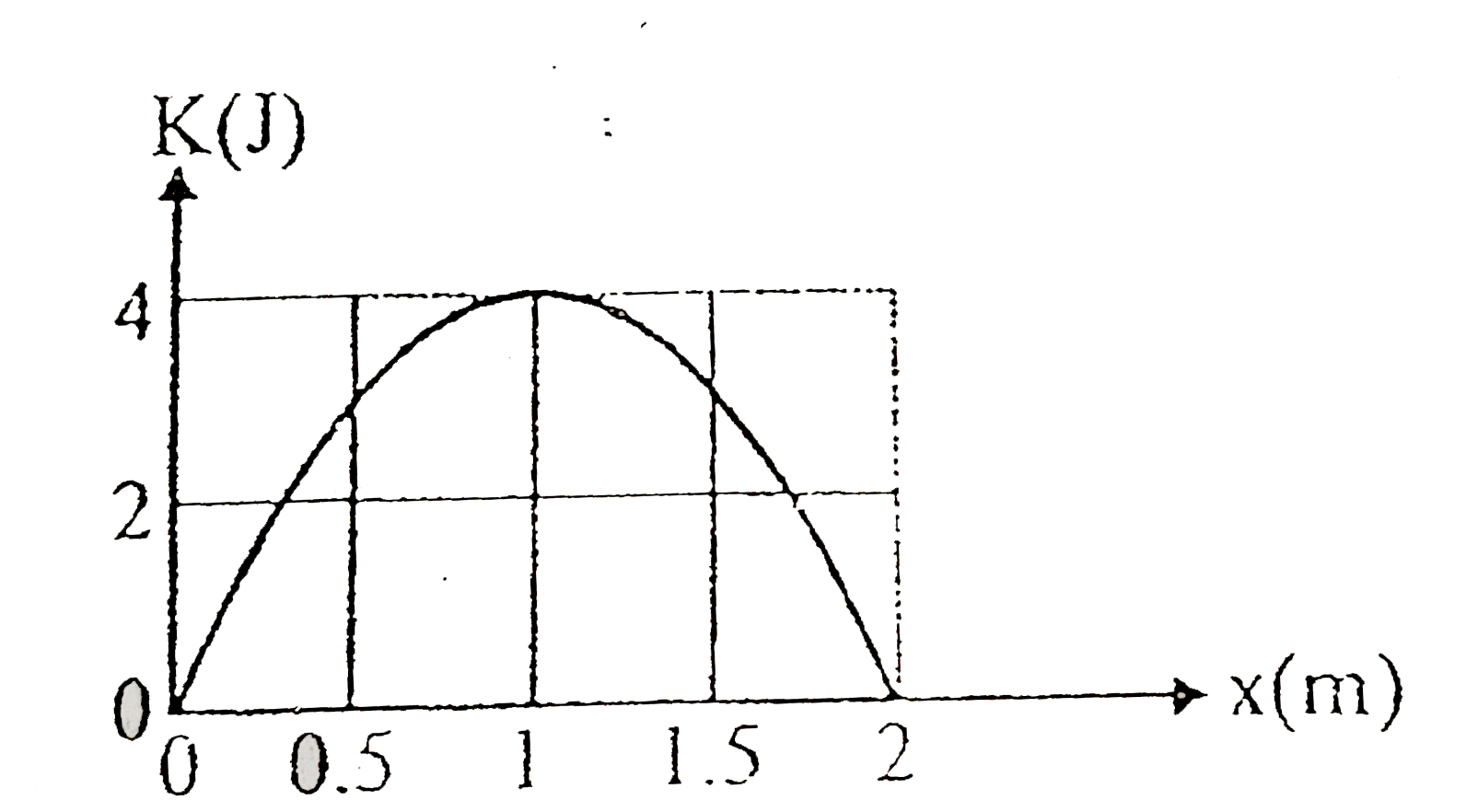
View SolutionA block of mass lies on a horizontal frictionless surface and is attached to one end of a horizontal spring (with spring constant ) whose other end is fixed . The block is intinally at rest at the position where the spring is unstretched . When a constant horizontal force in the positive direction of the axis is applied to it, a plot of the resulting kinetic energy of the block versus its position is shown in figure. What is the magnitude of ?
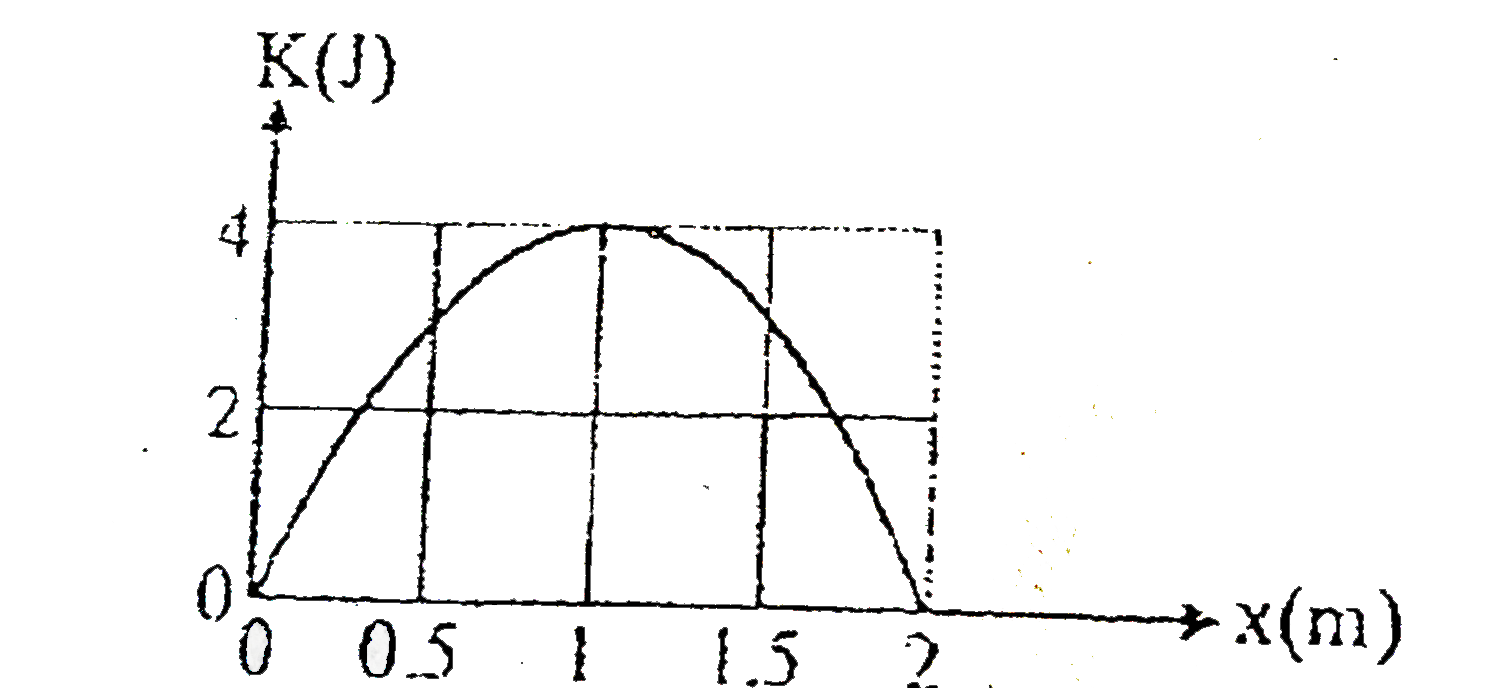
View SolutionA block of mass lies on a horizontal frictionless surface and is attached to one end of a horizontal spring (with spring constant ) whose other end is fixed . The block is intinally at rest at the position where the spring is unstretched . When a constant horizontal force in the positive direction of the axis is applied to it, a plot of the resulting kinetic energy of the block versus its position is shown in figure. What is the magnitude of ?
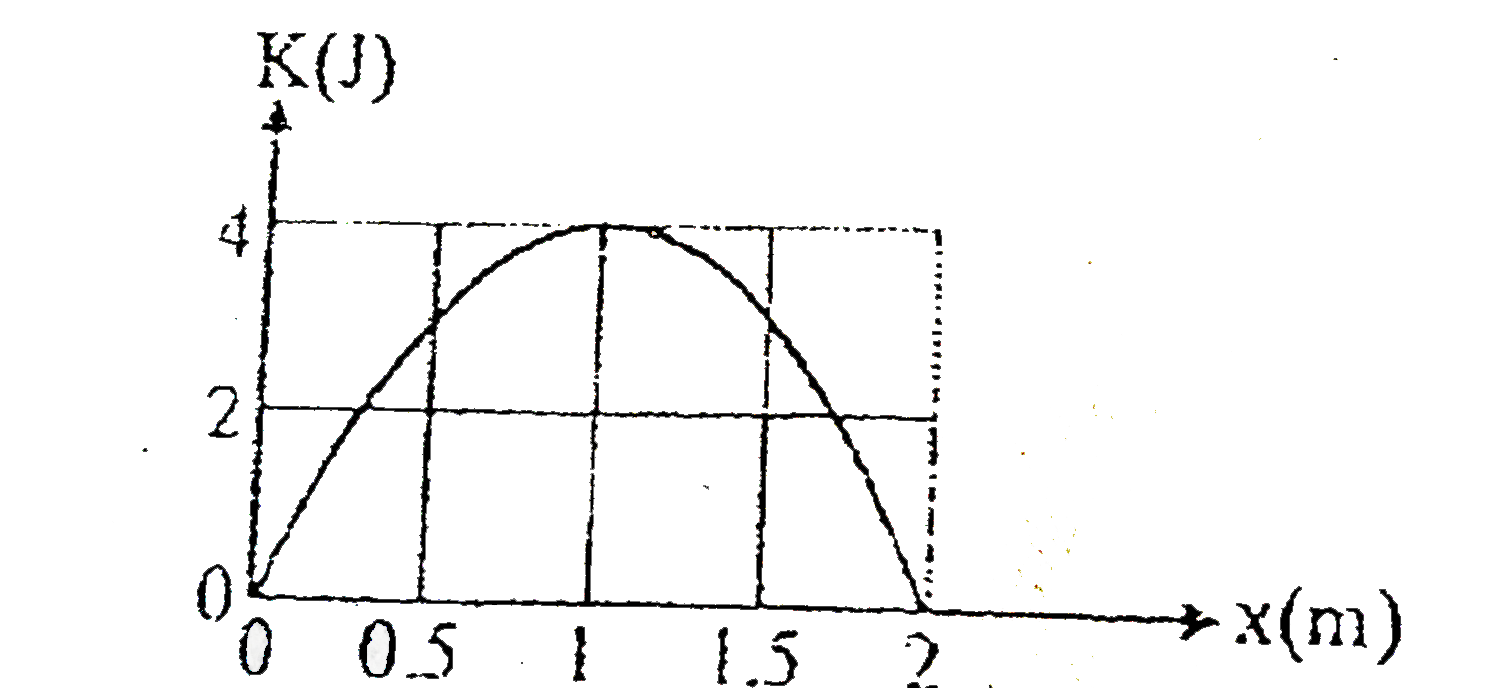
View SolutionA block of mass lies on a horizontal frictionless surface and is attached to one end of a horizontal spring (with spring constant ) whose other end is fixed . The block is intinally at rest at the position where the spring is unstretched . When a constant horizontal force in the positive direction of the axis is applied to it, a plot of the resulting kinetic energy of the block versus its position is shown in figure. What is the magnitude of ?
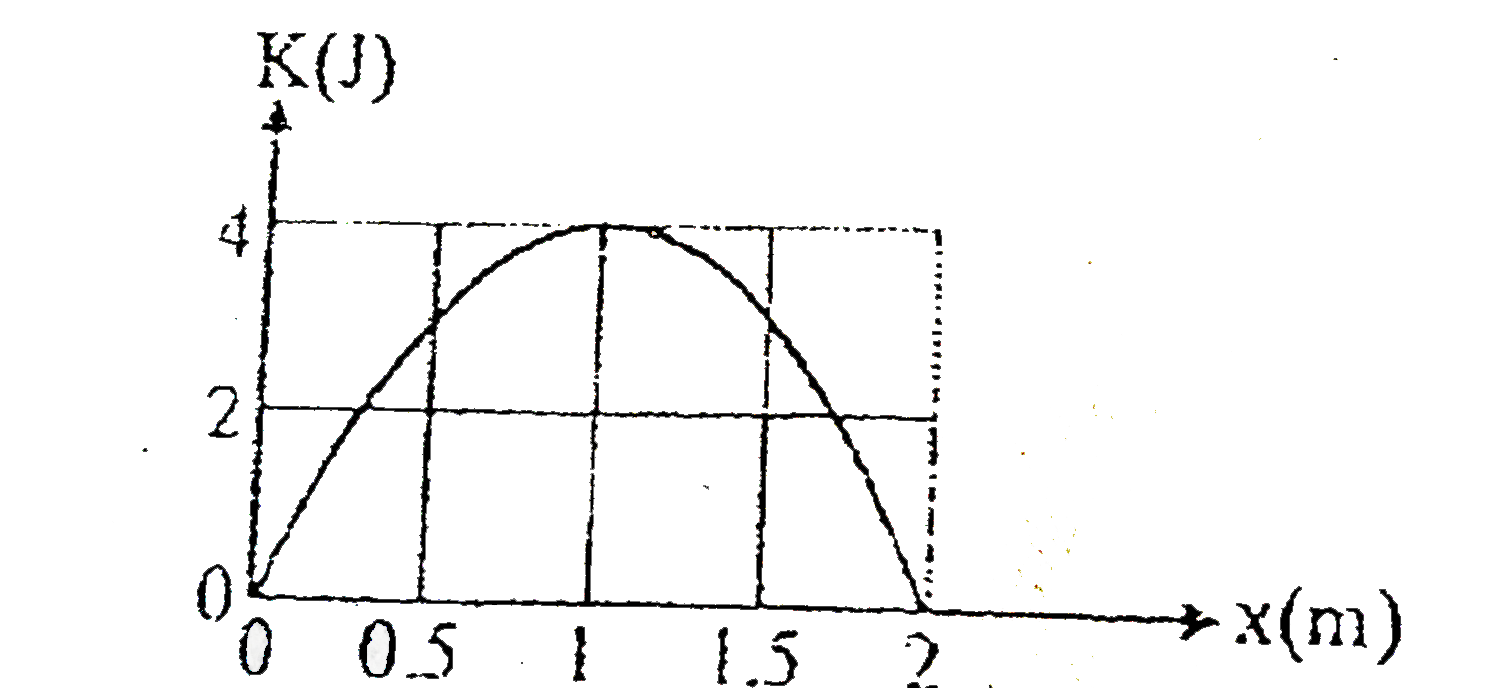
View Solution