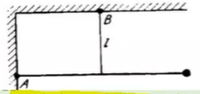
A thin perfectly rigid weightless rod with a point-like ball fixed at one end is deflected through a small angle a from its equilibrium position and then released. At the moment when the rod forms an angle β < α with the vertical the ball undergoes a perfectly elastic collision with an inclined wall Fig. 47.Determine the ratio T1/T of the period of oscillations of this pendulum to the period of oscillations of a simple pendulum having the same length.
In the absence of the wall the angle of deflection of the simple pendulum varies harmonically with a period T and an angular amplitude α. The projection of the point rotating in a circle of radius α at an angular velocity ω = 2pi/T performs the same motion. The perfectly elastic collision of the rigid rod with the wall at an angle of deflection corresponds to an instantaneous jump from point B to point C Fig. 185. The period is reduced by Δt = 2γ/ω where γ = arccos β/α. Consequently and the sought solution is
Related Solutions
A ball wall PQ which is vertical alpha Inclined at an angle, but suspended at the point by a string of length L. The string with the ball is now at a slight angle away from the vertical wall. beta If the ball is released, find the time of oscillation of the pendulum, when beta lt alpha Let the collision on the wall be perfectly elastic.
View SolutionA weightless rigid rod with a load at the end is hinged at point A to the wall so that it can rotate in all directions (Fig).
The rod is kept in the horizontal position by a vertical inextensible thread of length 1, fixed at its midpoint. The load receives a momentum in the direction perpendicular to the plane of the figure.
Determine the period T of small oscillations of the system.
View SolutionA weightless rigid rod with a load at the end is hinged at point A to the wall so that it can rotate in all directions (Fig).

The rod is kept in the horizontal position by a vertical inextensible thread of length 1, fixed at its midpoint. The load receives a momentum in the direction perpendicular to the plane of the figure.
Determine the period T of small oscillations of the system.
View SolutionA weightless rigid rod with a load at the end is hinged at point A to the wall so that it can rotate in all directions (Fig).

The rod is kept in the horizontal position by a vertical inextensible thread of length 1, fixed at its midpoint. The load receives a momentum in the direction perpendicular to the plane of the figure.
Determine the period T of small oscillations of the system.
View SolutionA ball is suspended by a thread of length L at a point O on a wall inclined at an angle a to the vertical. angle smaller than the vertical to the thread with the ball beta Displaced by 80 and also kept away from the wall. If the ball is released, what will be the time period of oscillation of the pendulum when beta gt alpha Is
View SolutionA simple pendulum has time period T. A uniform rod, whose length is the same as that of the pendulum, undergoes small oscillations about its upper end. Its time period of oscillation will be -
View Solutionएकसमान घनत्व वाली एक पतली छड़ एक किनारे के परिह : छोटे दोलन करती हैं। इसका आवर्तकाल है। यदि दोगुनी लम्बाई की ऐसी ही छड़ को दोलन करने दे, तो आवर्तकाल होगा
View SolutionA thin rod of length L is hanging from one end and free to oscillate like s compound pendulum about a horizontal axis, Its time period for small oscillations is
View SolutionA uniform rod of mass m and length l performs small oscillations about the horizontal axis passing through its upper end. FInd the mean kinetic energy of the rod averaged over the oscillation period if at the initial moment it was deflected from the vertical by an angle and then imparted an angular vertical .
View SolutionA ball is suspended by a thread of length l at the point O on an incline wall as shown. The inclination of the wall with the vertical is α.The thread is displaced through a small angle β away from the vertical and the ball is released. Find the period of oscillation of pendulum. Consider both cases a. alpha gt beta b. alpha lt beta Assuming that any impact between the wall and the ball is elastic.
View SolutionA ball is suspended by a thread of length l at the point O on an incline wall as shown. The inclination of the wall with the vertical is α.The thread is displaced through a small angle β away from the vertical and the ball is released. Find the period of oscillation of pendulum. Consider both cases a. alpha gt beta b. alpha lt beta Assuming that any impact between the wall and the ball is elastic.
View Solutionएक सरल लोलक के धात्विक गोलक पर ऋणावेश है तथा लोलक का आवर्तकाल T है | यदि इसे धनावेशित धात्विक प्लेट के ऊपर दोलित किया जाये तो इसका आवर्तकाल होगा
View SolutionA simple pendulum oscillating with a small amplitude has a time period of T = 1.0s . A horizontal thin rod is now placed beneath the point of suspension at a distance equal to half the length of the pendulum. The string collides with the rod once in each oscillation and there is no loss of energy in such collisions. Find the new time period T of the pendulum
View SolutionA ball falls vertically on an inclined plane of inclination alpha with speed v_0 and makes a perfectly elastic collision. What is angle of velocity vector with horizontal after collision.
View SolutionA ball falls vertically on an inclined plane of inclination alpha with speed v_0 and makes a perfectly elastic collision. What is angle of velocity vector with horizontal after collision.
View SolutionTwo identical simple pendulums each of length 'l' are connected by a weightless spring as shown. In equilibrium, the pendulums are vertical and the spring is horizontal and undformed. The time period of small oscillations of the linked pendulums, when they are deflected form their equilibrium positive through equal displacements in the same vertical plane in the opposite directions and released, is
View SolutionA thin uniform rod of length l is welded through its upper end. It is freely rotated in the vertical plane. Its time period for small amplitude oscillations will be:
View SolutionA uniform rod ofmass M and length L is hanging from its one end free to rotate in a veritcal plane.A small ball of equal mass is attached of the lowe end as shown. Time period of small oscillations of the rod is
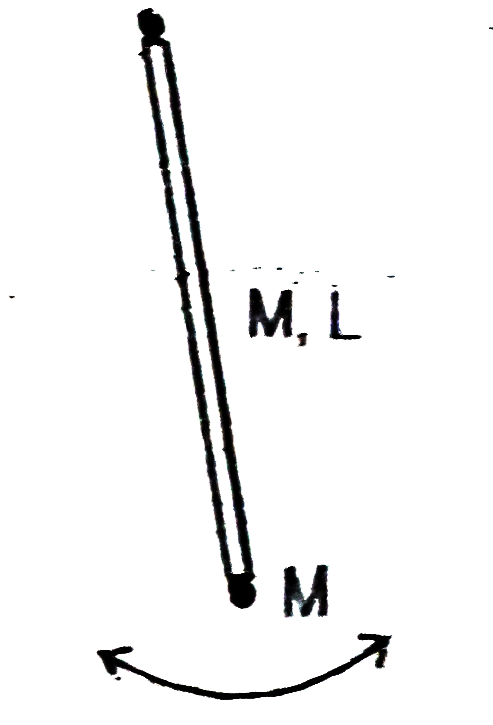
View SolutionA uniform rod ofmass M and length L is hanging from its one end free to rotate in a veritcal plane.A small ball of equal mass is attached of the lowe end as shown. Time period of small oscillations of the rod is
View SolutionA small bob attached to a light inextensible thread of length has a periodic time when allowed to vibrate as a simple pendulum. The thread is now suspended from a fixed end of a vertical rigid rod of length . If now the pendulum performs periodic oscillations in this arrangement, the periodic time will be

View Solution