Consider a block of conducting material of resistivity ρ shown in the figure. Current I enters at A and leaves from D.We apply superposition principle to find voltage ΔV developed between B and C. The calculation is done in the following stepsa Take current I entering from A and assume it to spread over a hemispherical surface on the block.b Calculate field Er at distance r from A by using Ohms law = ρJ where J is the current per unit area at r.c From the r dependence of Er obtain the potential Vr at r.d Repeat steps i ii and iii for current I leaving D and superpose results for A and D.ΔV measured between B and C is
The correct Answer is:Option
Correct Option cExplanation:Electric field at a distance r from A is
Related Solutions
Passage-II:
Consider a block conducting material of resistivity .. shown in the figure. Current .I. enters at .A. and leaves from .D.. We apply superposition principle to find voltage .. developed between .B. and .C.. The calculation is done in the following steps :
i) Take current .I. entering from .A. and assume it to spread over a hemispherical surface in the block.
ii) Calculate field E(r ) at distance .r. from A by using Ohm.s law , where j is the current per unit area at .r..
iii) From the .r. dependence of E(r ), obtain the potential V(r ) at r.
iv) Repeat (i), (ii), (iii) for current .I. leaving .D. and superpose results for .A. and .D..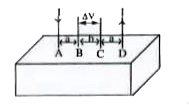
For current entering at A the electric field at a distance .r. from A is
View SolutionConsider a block of conducting material of resistivity shown in the figure. Current enters at 'A' and leaves from 'D'. We apply superposition principle to find voltage developed between 'B' and 'C'. The calculation is done in the following steps:
(i) Take current 'I' entering from 'A' and assume it to spread over a hemispherical surface in the block.
(ii) Calculate field E(r) at distance 'r' from A by using Ohm's law where j is the current per unit area at 'r'.
(iii) From the 'r' dependence of E(r), obtain the potential V(r) at r.
(iv) Repeat (i), (ii) and (iii) for current 'I' leaving 'D' and superpose results for 'A' and 'D'.
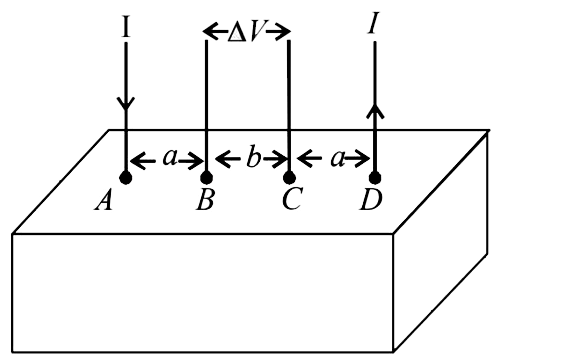
For current entering at A, the electric field at a distance 'r'
View SolutionConsider a block of conducting material of resistivity p shown in the figure. Current l enters at A and leaves from D. We apply superposition principle to find voltage developed between B and C.
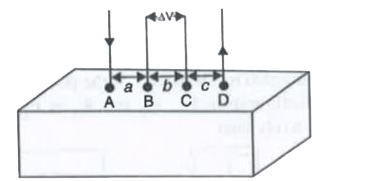
The calculation is done in the following steps :
(a) Take current I entering from A and assume it to spread over a hemispherical surface in the block.
(b) Calculate field E (r) at distance r from A by using Ohm's law E = pj, where j is the current per unit area at r.
(c) From the r dependence ofE (r), obtain the potential V (r) at r.
(d) Repeat (I), (ii) and (iii) for current l leaving D and superpose results for A and D.
For current entering at A, the electric field at a distance r from A is
View SolutionConsider a block of conducting material of resistivity shown in the figure. Current enters at 'A' and leaves from 'D'. We apply superposition principle to find voltage developed between 'B' and 'C'. The calculation is done in the following steps:
(i) Take current 'I' entering from 'A' and assume it to spread over a hemispherical surface in the block.
(ii) Calculate field E(r) at distance 'r' from A by using Ohm's law where j is the current per unit area at 'r'.
(iii) From the 'r' dependence of E(r), obtain the potential V(r) at r.
(iv) Repeat (i), (ii) and (iii) for current 'I' leaving 'D' and superpose results for 'A' and 'D'.
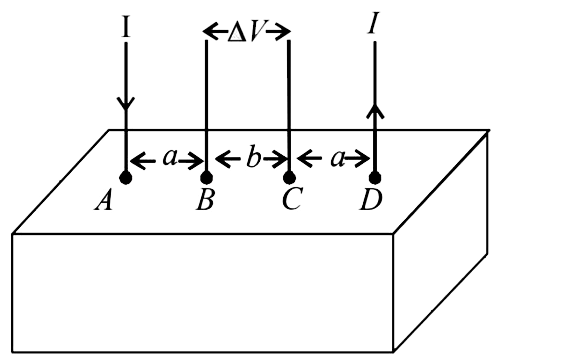
Delta V measured between B and C is
View SolutionConsider a block of conducting material of resistivity shown in the figure. Current enters at 'A' and leaves from 'D'. We apply superposition principle to find voltage developed between 'B' and 'C'. The calculation is done in the following steps:
(i) Take current 'I' entering from 'A' and assume it to spread over a hemispherical surface in the block.
(ii) Calculate field E(r) at distance 'r' from A by using Ohm's law where j is the current per unit area at 'r'.
(iii) From the 'r' dependence of E(r), obtain the potential V(r) at r.
(iv) Repeat (i), (ii) and (iii) for current 'I' leaving 'D' and superpose results for 'A' and 'D'.

Delta V measured between B and C is
View SolutionConsider a block of conducting material of resistivity p shown in the figure. Current l enters at A and leaves from D. We apply superposition principle to find voltage DeltaV developed between B and C. The calculation is done in the following steps : (a) Take current I entering from A and assume it to spread over a hemispherical surface in the block. (b) Calculate field E (r) at distance r from A by using Ohm's law E = pj, where j is the current per unit area at r. (c) From the r dependence ofE (r), obtain the potential V (r) at r. (d) Repeat (I), (ii) and (iii) for current l leaving D and superpose results for A and D. DeltaV measured between B and C is :
View Solutionचित्र में प्रतिरोधकता का एक चालक ब्लॉक है। धारा A पर प्रवेश कर D से बाहर आती है। हम B तथा C के बीच उत्पन्न विभवान्तर V ज्ञात करने के लिए अध्यारोपण का सिद्धान्त लगाते हैं। गणना निम्न चरणों में की जाती है

(i)A से प्रवेश करने वाली धारा को I लेते हैं तथा मानते हैं कि ब्लॉक के अन्दर यह अर्द्धगोलाकार पृष्ठ पर फैल 2001 जाता है। (ii) ओम के नियम E = J, जहाँ J एकांक क्षेत्रफल से प्रवाहित धारा है, को प्रयोग कर A से दूरी पर वैद्युत क्षेत्र E(r) ज्ञात करते हैं। (iii) E(r) की पर निर्भरता से दूरी पर विभव V(r) ज्ञात करते हैं। (iv) पद (i), (ii) तथा (ii) को D पर निर्गत धारा I के लिए दोहराते हैं तथा परिणाम को A तथा D पर प्रयोग करते हैं
A पर प्रवेश करने वाली धारा के लिए, A से r दूरी पर वैद्युत क्षेत्र
View Solutionचित्र में प्रतिरोधकता का एक चालक ब्लॉक है। धारा A पर प्रवेश कर D से बाहर आती है। हम B तथा C के बीच उत्पन्न विभवान्तर V ज्ञात करने के लिए अध्यारोपण का सिद्धान्त लगाते हैं। गणना निम्न चरणों में की जाती है

(i)A से प्रवेश करने वाली धारा को I लेते हैं तथा मानते हैं कि ब्लॉक के अन्दर यह अर्द्धगोलाकार पृष्ठ पर फैल 2001 जाता है। (ii) ओम के नियम E = J, जहाँ J एकांक क्षेत्रफल से प्रवाहित धारा है, को प्रयोग कर A से दूरी पर वैद्युत क्षेत्र E(r) ज्ञात करते हैं। (iii) E(r) की पर निर्भरता से दूरी पर विभव V(r) ज्ञात करते हैं। (iv) पद (i), (ii) तथा (ii) को D पर निर्गत धारा I के लिए दोहराते हैं तथा परिणाम को A तथा D पर प्रयोग करते हैं
B तथा C के बीच मापा गया V है
View Solutionपैरा 4
चित्र II.75 में दिखाया गया प्रतिरोधकता वाला चालक पदार्थ का एक गुटका लें। धारा , बिन्दु A से प्रवेश करती है और D से बाहर निकलती है। हम अध्यारोपण का नियम लगाकर B और C के बीच पैदा हुई वोल्टता निकालते हैं। यह इन चरणों में किया जाता है :
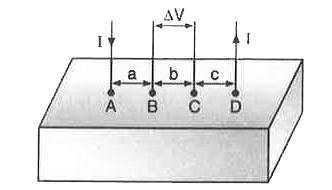
(i ) मान लें कि धारा, I, बिन्दु A से प्रवेश करती हैं और गुटके में एक गोलार्ध पृष्ठ पर फैली हुई है।
(ii) A से r दुरी पर क्षेत्र E(r) ओम का नियम प्रयुक्त करते हुए निकालें जहाँ j, r दूरी पर प्रति यूनिट क्षेत्रफल धारा है। की पर निर्भरता से पर विभव V (r) निकालें।
(iv) D से निकल रही धारा I के लिए (i), (ii) और (iii) को दोहराएँ औरA और D के लिए परिणामों का अध्यारोपण करें।
A पर प्रवेश करने वाली धारा के लिए A से r दूरी पर विद्युत क्षेत्र है
View SolutionAs shown in the figure 'rho' Consider a block of resistive conductive material. Section 'I' flows through 'A' and gets expelled from 'D'. We originated between 'B' and 'C' Delta V The principle of imputation is used to find the voltage. The calculation is done in the following terms. : (i) Assume Section 'I' entering from A and assume that it spreads above the semicircular surface in the block. (ii) Ohm's law E=rho j Calculate the electric field E (r) at the distance from A to r using the area j per unit area on 'r'. (iii) The dependence of E (r) on r gives the potential V (r) at r. (iv) Repeat (i), (ii) and (iii) for Section I issued from D and install the results for A and D. Measured between B and C Delta V is -
View SolutionIn the picture rho A driver of resistivity is the block. Entering section A and coming out of D. We generate the potential difference between B and C. DeltaV To make known, we apply the principle of imposition. The calculation is done in the following steps (i) I take the stream entering from A and assume that inside the block it spreads on a semicircular surface. (ii) Ohm's law E=rhoJ , Where J is the current flowing through the unit area, find the electric field E (r) at a distance from A to r. (iii) Determine the potential V (r) at r distance from the dependence of E (r) on r. (iv) Repeat the terms (i), (ii) and (iii) issued on D for Section I and use the result on A and D. For the current entering A, the electric field at a distance from A to r
View Solutionपैरा 4
चित्र II.75 में दिखाया गया प्रतिरोधकता वाला चालक पदार्थ का एक गुटका लें। धारा , बिन्दु A से प्रवेश करती है और D से बाहर निकलती है। हम अध्यारोपण का नियम लगाकर B और C के बीच पैदा हुई वोल्टता निकालते हैं। यह इन चरणों में किया जाता है :
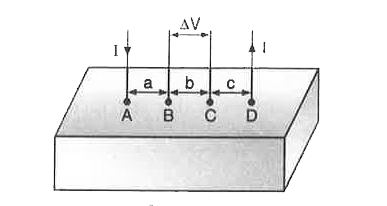
(i ) मान लें कि धारा, I, बिन्दु A से प्रवेश करती हैं और गुटके में एक गोलार्ध पृष्ठ पर फैली हुई है।
(ii) A से r दुरी पर क्षेत्र E(r) ओम का नियम प्रयुक्त करते हुए निकालें जहाँ j, r दूरी पर प्रति यूनिट क्षेत्रफल धारा है। की पर निर्भरता से पर विभव V (r) निकालें।
(iv) D से निकल रही धारा I के लिए (i), (ii) और (iii) को दोहराएँ औरA और D के लिए परिणामों का अध्यारोपण करें।
B और C के बीच मापा गया है
View Solutionआरेख में दर्शाए प्रतिरोधकता के चालक पदार्थ से बने किसी गुटके परविचार कीजिए। धारा 'I', 'A' पर प्रवेश करती है तथा 'D' से निकलती है। 'B' तथा 'C' के बीच विकसित वोल्टता को ज्ञात करने के लिए हम अध्यारोपण सिद्धांत का अनुप्रयोग करते हैं। इसमें परिकलन निम्नलिखित चरणों में किए गए हैं।
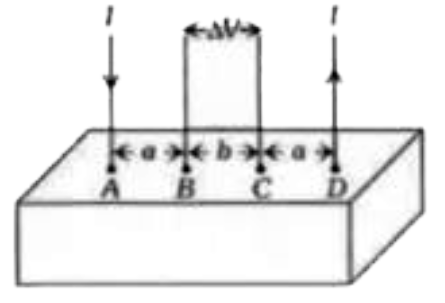
(i) धारा 'I' को 'A' से प्रवेश करते हुए लीजिए तथा यह मानिए कि यह गुटके में अर्धगोलीय पृष्ठ पर फैल जाती है।
(ii) बिन्दु A से दूरी 'r' पर विद्युत-क्षेत्र E(r) का परिकलन ओम के नियम , जहाँ j, दूरी 'r' पर धारा प्रति एकांक क्षेत्रफल है, का उपयोग करके कीजिए।
(iii) E (r) की 'r' पर निर्भरता द्वारा r पर विभव V(r) प्राप्त कीजिए।
(iv) 'D' पर धारा 'I' निकालने के लिए चरणों (i), (ii) तथा (iii) को दोहराइए तथा 'A' तथा 'D' के परिणामों का अध्यारोपण कीजिए।
A पर धारा के प्रवेश के लिए, A से 'r' दूरी पर विद्युत-क्षेत्र है
View SolutionAs shown in the figure 'rho' Consider a block of resistive conductive material. Section 'I' flows through 'A' and gets expelled from 'D'. We originated between 'B' and 'C' Delta V The principle of imputation is used to find the voltage. The calculation is done in the following terms. : (i) Assume Section 'I' entering from A and assume that it spreads above the semicircular surface in the block. (ii) Ohm's law E=rho j Calculate the electric field E (r) at the distance from A to r using the area j per unit area on 'r'. (iii) The dependence of E (r) on r gives the potential V (r) at r. (iv) Repeat (i), (ii) and (iii) for Section I issued from D and install the results for A and D. For the current entering from A, the electric field at the distance 'r' from A is -
View SolutionTwleve equal wires , each of resistance r ohm , are connected so as to form a frame of a cube . An electric current enters this cube at one corner and leaves from the diagnalyy opposite corner . Calculate the total resisatance between the corners .
View SolutionFigure shows a square loop of edge a made of a uniform wire. A current i enters the loop at the point A and leaves it at the point C. Find the magnetic field at the point P which is on the perpendicular bisector of AB at a distance a/4 from it.
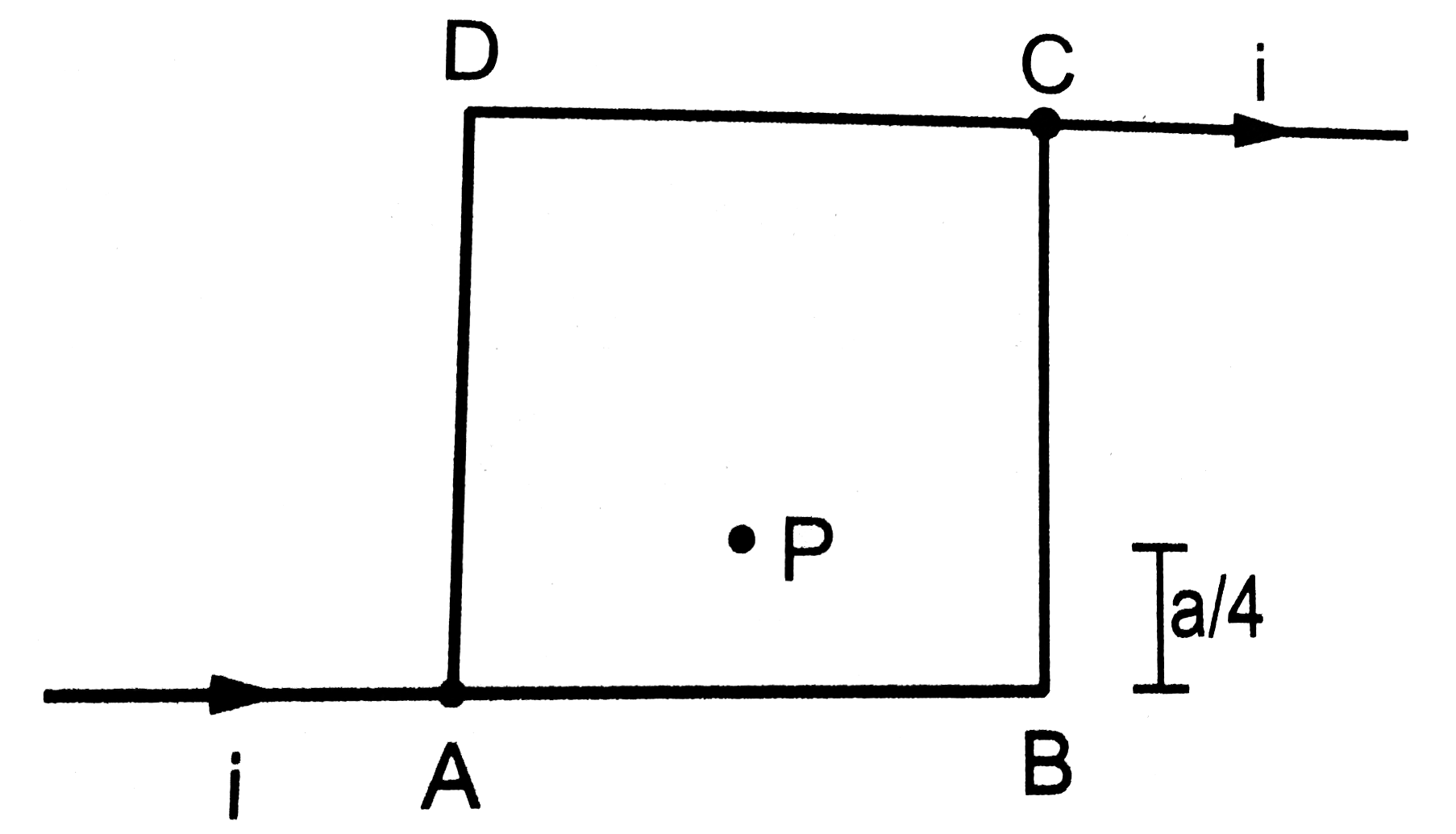
View SolutionFigure shows a square loop of edge a made of a uniform wire. A current i enters the loop at the point A and leaves it at the point C. Find the magnetic field at the point P which is on the perpendicular bisector of AB at a distance a/4 from it.

View SolutionFigure shows a square loop of edge made of a uniform wire. A current enters the loop at the point A and leaves it at the point C. Find the magnetic field at the point P which is on the perpendicular bisector of AB at a distance a/4 from it.

View SolutionFrom the graph between current (I) and voltage (V) as shown in the figure, identify the portion correspoindgin to negative resistance
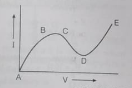
View SolutionFrom the given between current I and voltage V shown in figure , indentify the portion corresponding to negative resistance
View Solution