A uniform horizontal circular disc of mass M and radius R can freely rotate about a vertical axle passing through its centre. A particle of mass m is initially placed near the centre of the disc in a smooth groove made along the radius of the disc as shown. An initial angular velocity w0 is imparted to the disc. Find the angular velocity of the disc when the particle reaches the other end of the groove.
Related Solutions
A uniform disc of mass m and radius R rotates about a fixed vertical axis passing through its centre with angular velocity omega . A particle of same angular velocity mass m and moving horizontally with velocity 2omegaR towards centre of the disc collides and sticks to its rim. The impulse on the particle due to the disc is
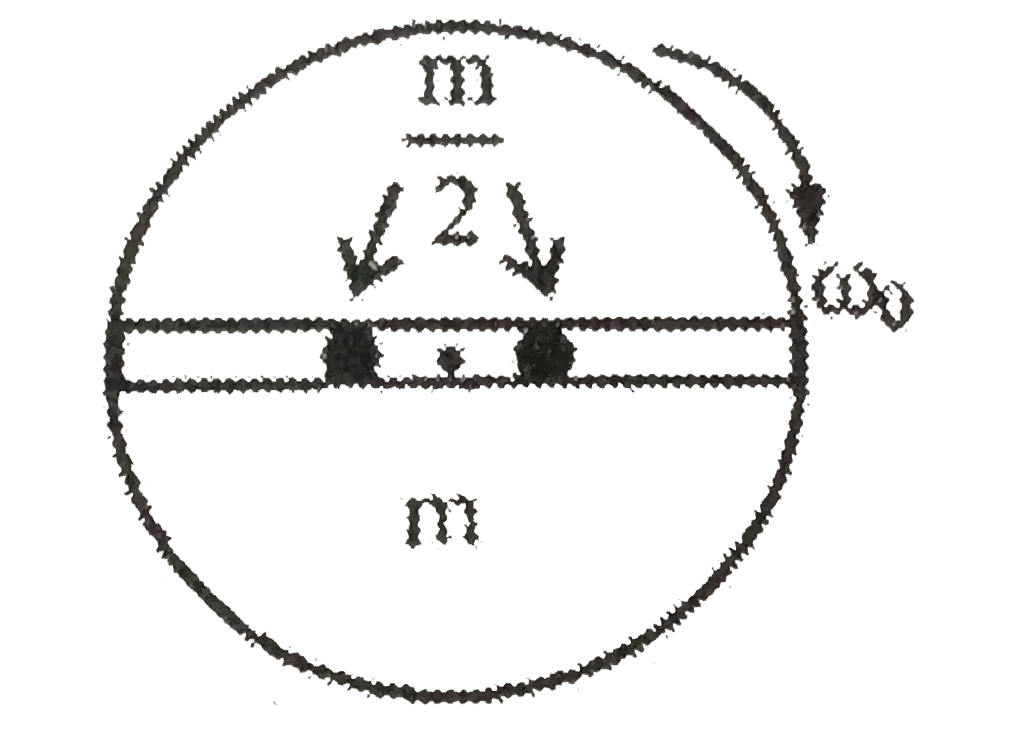
View SolutionA disc of mass m and radius R is free to rotate in a horizontal plane about a vertical smooth fixed axis passing through its centre. There is a smooth groove along the diameter of the disc and two small balls of mass m//2 each are placed in it on either side of the centre of the disc as shown in Fig. The disc is given an initial angular velocity omega_(0) and released. The angular speed of the disc when the balls reach the end of the disc is
View SolutionA disc of mass and radius is free to rotate in a horizontal plane about a vertical smooth fixed axis passing through its centre. There is a smooth groove along the diameter of the disc and two small balls of mass each are placed in it on either side of the centre of the disc as shown in Fig. The disc is given an initial angular velocity and released.

The angular speed of the disc when the balls reach the end of the disc is
View SolutionA man of mass stands on a horizontal platform in the shape of a disc of mass and radius , pivoted on a vertical axis thorugh its centre about which it can freely rotate. The man starts to move aroung the centre of the disc in a circle of radius with a velocity relative to the disc. Calculate the angular velocity of the disc.
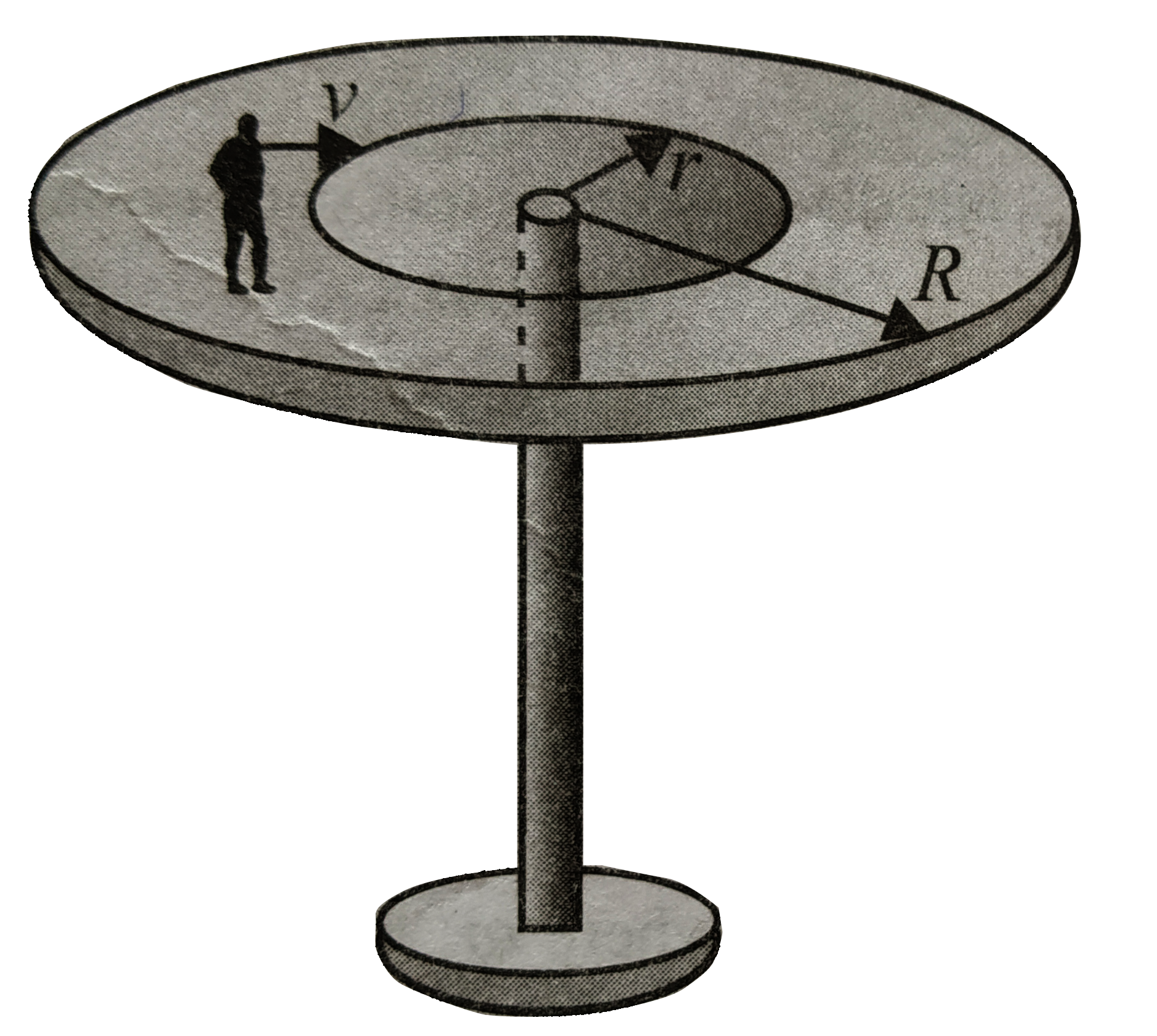
View SolutionA man of mass stands on a horizontal platform in the shape of a disc of mass and radius , pivoted on a vertical axis through its centre about which it can freely rotate. The man starts to move around the centre of the disc in a circle of radius with a velocity relative to the disc. Calculate the angular velocity of the disc.

View SolutionA uniform disc of mass m and radius R rotates about a fixed vertical axis passing through its centre with angular velocity omega . A particle of same mass m and having velocity of 2omegaR towards centre of the disc collides with the disc moving horizontally and sticks to its rim. Then
View SolutionA uniform disc of mass m and radius R rotates about a fixed vertical axis passing through its centre with angular velocity omega . A particle of same mass m and having velocity of 2omegaR towards centre of the disc collides with the disc moving horizontally and sticks to its rim. Then
View SolutionA disc of mass 'm' and radius R is free to rotate in horizontal plane about a vetical smooth fixed axis passing through is centre. There is a smooth groove along the diameter of the disc and two small balls of mass m/2 each are placed in it on either side of the centre of the disc as shown in fig. The disc is given initial angular velocity and released. The angular speed of the disc when the balls reach the end of the disc is -
View SolutionA thin uniform circular disc of mass M and radius R is rotating in a horizontal plane about an axis passing through its centre and perpendicular to its plane with an angular velocity omega . Another disc of same dimensions but of mass (1)/(4) M is placed gently on the first disc co-axially. The angular velocity of the system is
View SolutionA thin uniform circular disc of mass M and radius R is rotating in a horizontal plane about an axis passing through its centre and perpendicular to its plane with an angular velocity omega . Another disc of same dimensions but of mass M/4 is placed gently on the first disc coaxially. The angular velocity of the system now is
View SolutionA thin uniform circular disc of mass M and radius R is rotating in a horizontal plane about an axis passing through its centre and perpendicular to its plane with an angular velocity omega . Another disc of same dimensions but of mass (1)/(4) M is placed gently on the first disc co-axially. The angular velocity of the system is
View SolutionA horizontal disc rotates freely about a vertical axis through its centre. A ring having the same mass and radius as the disc is now gently placed on the disc After same time, the two rotate with a common angular velocity
View SolutionA horizontal disc rotates freely about a vertical axis through its centre. A ring, having the same mass and radius as the disc, is now gently placed on the disc. After some time, the two rotate with a common angular velocity, then
View SolutionA disc of mass m and radius R is free to rotate in a horizontal plane about a vertical smooth fixed axis passing through its centre. There is a smooth groove along the diameter of the disc and two small balls of mass m//2 each are placed in it on either side of the centre of the disc as shown in Fig. The disc is given an initial angular velocity omega_(0) and released. The net work done by forces exerted by the disc on the ball for the duration ball remains on the disc is
View SolutionA uniform disc of radius a and mass m, is rotating freely with angular speed omega in a horizontal plane about a smooth fixed vertical axis through its centre. A particle, also of mass m, is suddenly attached to the rim of the disc of the disc and rotates with it. The new angular speed is
View SolutionA uniform disc of radius a and mass m, is rotating freely with angular speed in a horizontal plane. About a smooth fixed vertical axis through its centre. A particle, also of mass m, is suddently attached to the rim of the disc of the disc and rotates with it. The new angular speed is
View SolutionA disc of mass and radius 6 metre is free to rotate in horizontal plane about a vertical fixed axis passing through its centre. There is a smooth groove along the diameter of the disc and two small balls of mass omega_(0)=12 (rad) / (s) released. Find the angular speed of disc (in radian/s) when the balls reach the ends to disc.
'(##CEN_KSR_PHY_JEE_C09_E01_016_Q06##)'
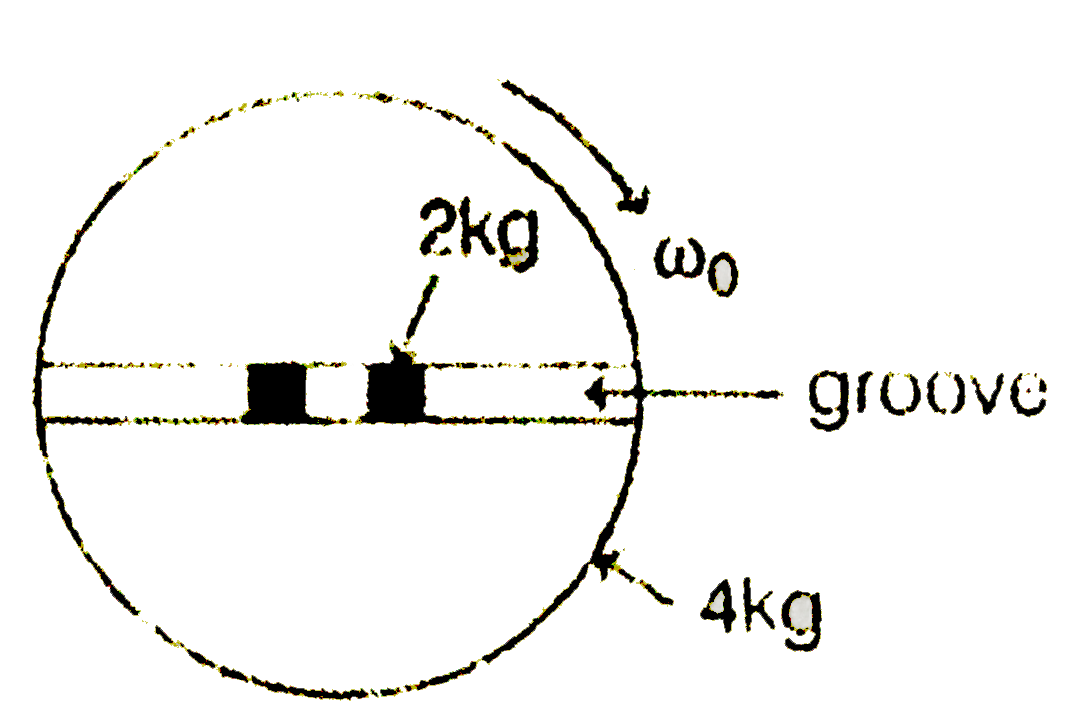
View SolutionA disc of mass 4 kg and radius 6 metre is free to rotate in horizontal plane about a vertical fixed axis passing through its centre. There is a smooth groove along the diameter of the disc and two small blocks of masses 2 kg each are placed in it on either side of the centre of the disc as shown in figure. The disc is given initial angular velocity omega_(0) =12 rad/sec and released. Find the angular speed of disc (in radian/sec) when the blocks reach the ends of the disc.
View SolutionA disc of mass 4 kg and radius 6 metre is free to rotate in horizontal plane about a vertical fixed axis passing through its centre. There is a smooth groove along the diameter of the disc and two small blocks of masses 2 kg each are placed in it on either side of the centre of the disc as shown in figure. The disc is given initial angular velocity =12 rad/sec and released. Find the angular speed of disc (in radian/sec) when the blocks reach the ends of the disc.
View SolutionA horizontal disc rotates freely with angular velocity about a vertical axis through its centre. A ring, having the same mass and radius as the disc, is gently placed on the dics. The common angular velocity with which the two ratate will be,
View Solution