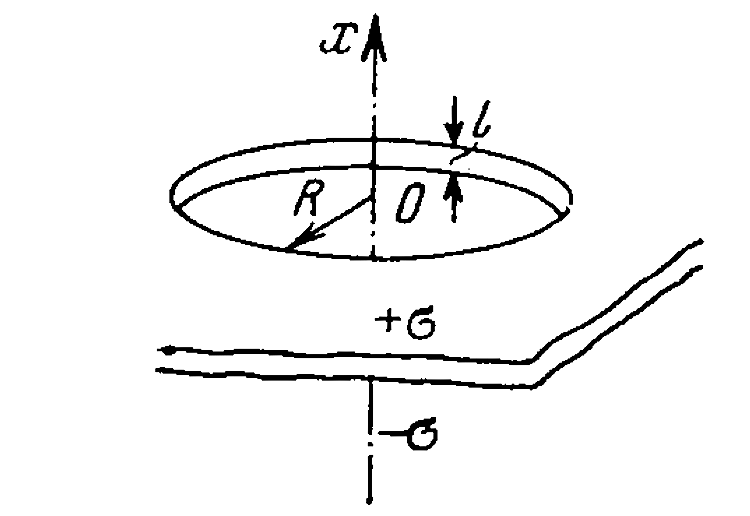
Two infinite planes separated by a distance l carry a uniform surface charge of densities σ and —σ Fig. 3.7. The planes have round coaxial holes of radius with l << R. Taking the origin O and the x coordinate axis as shown in the figure find the potential of the electric field and the projection of its strength vector Ex on the axes of the system as functions of the x coordinate. Draw the approximate plot φ x.
The field of a pair of oppositely changed sheets with holes can by superposition be reduced to that of a pair of uniform opposite charged sheets and discs with opposite charges. Now the charged sheets do not contribute any field outside them. Thus using the result of the previous problem
Related Solutions
Two infinite planes sepated by a distance carrying a uniform surface charge of densities and . The planes have round coaxial holes of radius , with . Taking the origin and the cordinates axis as shown in the figure, find the potentail of the electric field and the projection of its strength vector on the area of the system as functions of the x cordiante. Draw the appoximate plot .
View SolutionTwo coaxial rings, eacg of radius R, made of thin wire are separated by a small distabce l(l lt lt R) and carry the charges q and -q . Find the electric field potential and strength at the axis of the system as a function of the x coordinate (see figure). Investigate these functions at |x| gt gt R
View SolutionTwo coaxial rings, eacg of radius R, made of thin wire are separated by a small distabce l(l lt lt R) and carry the charges q and -q . Find the electric field potential and strength at the axis of the system as a function of the x coordinate (see figure). Investigate these functions at |x| gt gt R
View SolutionA very thin round plate of radius R carrying a uniform surface charge density sigma is located in vacumm. Find the electric field potentail and strength along the plate's axis as a function of a distance l from its centre. Investigation the obtained expression of l rarr 0 and l gt gt R .
View SolutionTwo this parallel threads carry a uniform charge with linear densities lamnda and -lambda . The distance between the threads is equal to l . Find the potential of the electric field and the magnitude of its strength vector at the distance r gt gt l at the angle theta to the vector 1 (fig).
View SolutionTwo infinite plane parallel sheets separated by a distance d have equal and opposite uniform charge densities o. Electric field at a point between the sheets is
View SolutionA thin wire ring of radius R carries a charge q . The ring si oriented parallel to an infinite conducting plane and is spearated by a distance l from it. Find : (a) the surface chagre density at that point fo the plane symmetrical with respect to the ring, (b) the strength and the potential of the electric field at the centre of the ring.
View SolutionA uniformly charged disc of radius R having surface charge density is placed in the xy plane with its center at the origin. Find the electric field intensity along the z-axis at a distance Z from origin :
View SolutionWhich is the correct formula for surface charge density (σ)
View SolutionTwo infinite parallel planes have uniform charge densities . What is the electric field in the region between the planes
View SolutionTwo infinite plane parallel sheets, separated by a distance d have equal and opposite uniform charge densities . Electric field at a point between the sheets is
View SolutionTwo infinite plane parallel sheets, separated by a distance d have equal and opposite uniform charge densities . Electric field at a point between the sheets is
View SolutionTwo point charges q and -q are separated by the distance l , both being located at a distance l//2 from the infinite conducting plane. Find : (a) the modulus of the electric force acting on each charge, (b) the magnitude of the electric field strength vector at the midpoint between these charges.
View SolutionA thin wire of radius ..r.. carries a charge q. Find the magnitude of the electric field strength on the axis of the ring as a function of distance L from the centre. Find the same for Find maximum field strength and the corresponding distance L.
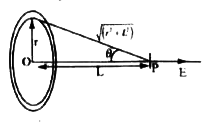
View SolutionA thin wire ring of radius "r" carries a charge q. Find the magnitude of the electric field strength on the axis of the ring as a function of distance L from the centre. Find the same for L gtgt r. Find maximum field strength and the corresponding distance L.
View SolutionA thin wire of radius ..r.. carries a charge q. Find the magnitude of the electric field strength on the axis of the ring as a function of distance L from the centre. Find the same for L gt gt r Find maximum field strength and the corresponding distance L.
View SolutionA uniformly charged disc of radius R with surface charge density R is placed in the xy plane, whose center is at the origin. Find the intensity of the electric field along the 2-axis at a distance Z from the origin.
View SolutionTwo infinitely large charged planes having uniform surface change density + and - are placed along xy plane and yz plane resp as shown in figure. Then nature of electric lines of force in xz plane is given by
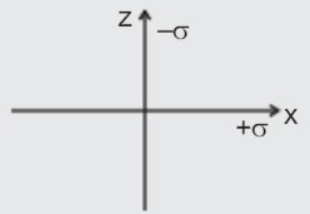
View SolutionTwo infinitely large charged planes having uniform surface change density + sigma and - sigma are placed along xy plane and yz plane resp as shown in figure. Then nature of electric lines of force in xz plane is given by
View SolutionA uniform electric field exists in x y plane as shown in Fig. 3.45. Find the potential difference. Between origin O and .
 .
.
View Solution