An ideal gas with the adiabatic exponent γ goes through a direct clockwise cycle consisting of adiabatic isobaric and isochoric lines. Find the efficiency of the cycle if in the adiabatic process the volume of the ideal gasa increases n-fold; b decreases n-fold.
Along the adiabatic line TVγ-1 = constant
Related Solutions
An ideal gas with the adiabatic exponent y goes through a direct (clockwise) cycle, consisting of adiabatic, isobaric and isochoric lines. Find the efficiency of the cycle if in the adiabatic process the volume of the ideal gas increases n fold.
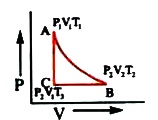
View SolutionAn ideal gas with the adiabatic exponent goes through a direct (clockwise) cycle conisting of adiabatic, isobaric, and isochoric lines. Find the efficiency of the cycle if in the adiabatic process the volume of the ideal gas.
(a) increases n-fold ,
(b) decreases n-fold.
View SolutionCalculate the efficiency of a cycle consisting of isothermal, isobaric, and isochoric line, if in the isothermal process the volume of the ideal gas with the adiabatic exponent .
(a) increased ,
(b) decreases .
View SolutionAn ideal gas goes through a cycle consisting of (a) isochoric, adiabatic, and isothermal lines , (b) isobaric, adiabatic, and isothermal lines, with the isothermal process proceeding at the minimum temperature of the whole cycle. Find the efficiency of each cycle if the absolute temperature varies n-fold within the cycle.
View SolutionFind the efficiency of a cycle consisting of two isobaric and two isothermal lines if the pressure varies and the absolute temperature within the cycle. The working substance is an ideal gas with the adiabatic exponent .
View SolutionFind the efficiency of a cycle consisting of two isochoric and two isothermal lines if the volume varies and the absolute temperature within the cycle. The working substance is an ideal gas with the adiabatic exponent .
View SolutionOne mole of an ideal gas is carried through a thermodynamics cycle as shown in the figure. The cycle consists of an isochoric, an isothermal and an adiabatic process. Find the adiabatic exponent of the gas.
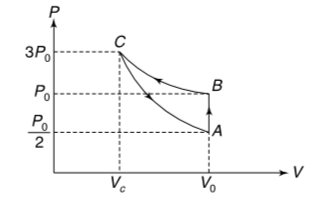
View SolutionAn ideal gas goes through a cycle consisting of isothermal, polytropic, and adiabatic lines, with the isothermal process proceeding at the maximum temperature of the whole cycle. Find the efficiency of such a cycle if the absolute temperature varies within the cycle.
View SolutionAn ideal gas with the adiabatic exponent gamma goes through a cycle (Fig. 2.3) within which the absolute temperature varies tau-fold . Find the efficiency of this cycle. .
View SolutionFind the efficiency of a cycle consisting of two isobaric and two adiabatic lines, if the pressure changes times within the cycle. The working substance is an ideal gas whose adiabatic exponent is equal to .
View SolutionAn ideal gas whose adiabatic exponent equals goes through a cycle consisting of two isochoric and two isobaric lines. Find the efficiency of such a cycle, if the absolute temperature of the gas rises times both in a isochoric heating and in the isobaric expansion.
View SolutionA gas (gamma=1.5) undergoes a cycle of adiabatic, isobaric and isochoric processes in an order. If the volume of the gas is doubled in the adiabatic process then the efficiency of the cycle is approximately,
View SolutionFind the efficiency of a cycle consisting of two isochoric and two adiabatic lines if the volume of the ideal gas changes n=10 times within the cycle. The working gas has gamma=1.5 .
View SolutionOne mole of an ideal gas with the adiabatic exponent goes through a polytropic process as a result of which the absolute temperature of the gas increases . The polytropic constant equal . Find the entropy increment of the gas in this process.
View SolutionFind the efficiency of a cycle consisting of two isochoric and two adiabatic lines, if the volume of the ideal gas changes times within the cycle. The working substance is nitrogen.
View SolutionCalculate the efficiency of a cycle consisting of two isobaric and two adiabtic lines, if the pressure changes n=10 times within the cycle. The working substances is an ideal gas of adiabatic exponent gamma=1.5 .
View SolutionTwo moles of an ideal gas goes under the process shown in figure. AB and CD are reversible adiabatic process. The efficiency of the cycle is
View SolutionThe efficiency of an ideal gas with adiabatic exponent for the shown cyclic process would be
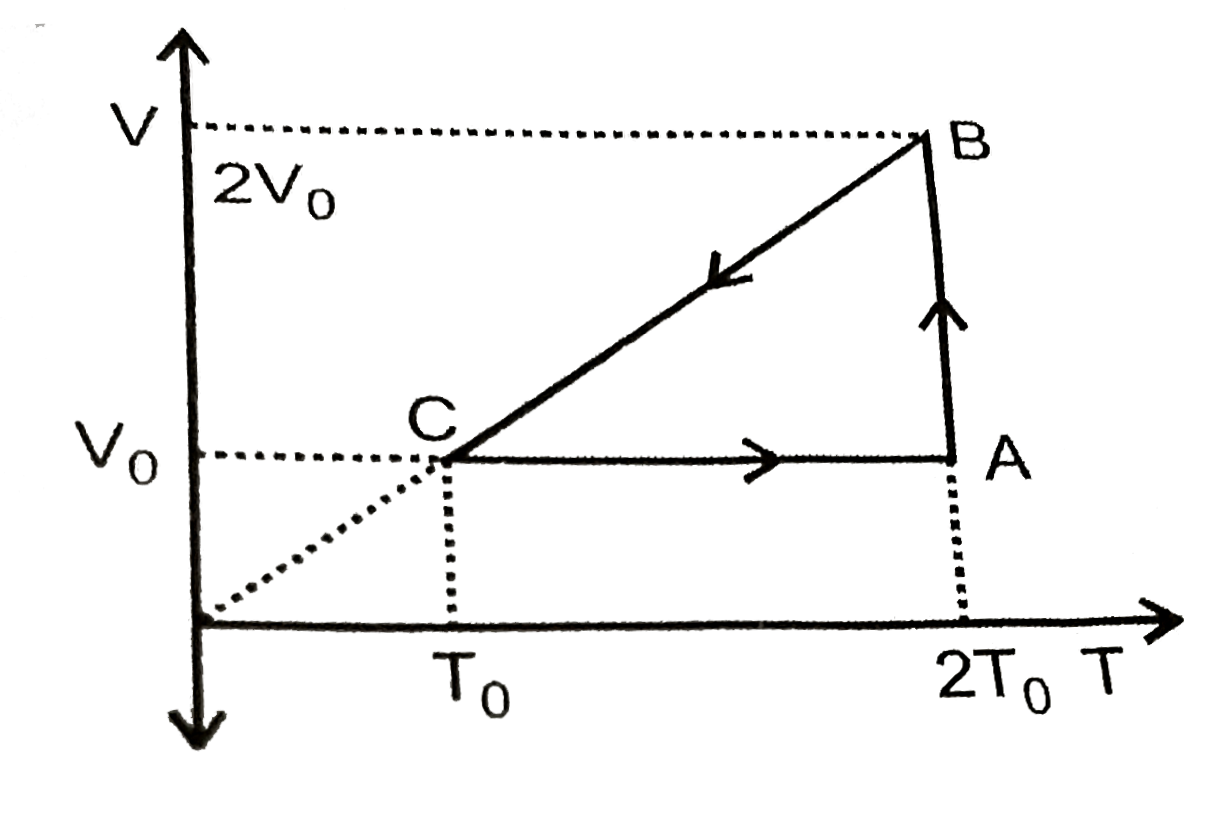
View SolutionThe efficiency of an ideal gas with adiabatic exponent 'gamma' for the shown cyclic process would be
View SolutionThe efficiency of an ideal gas with adiabatic exponent 'gamma' for the shown cyclic process would be
View Solution