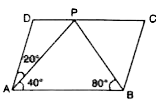
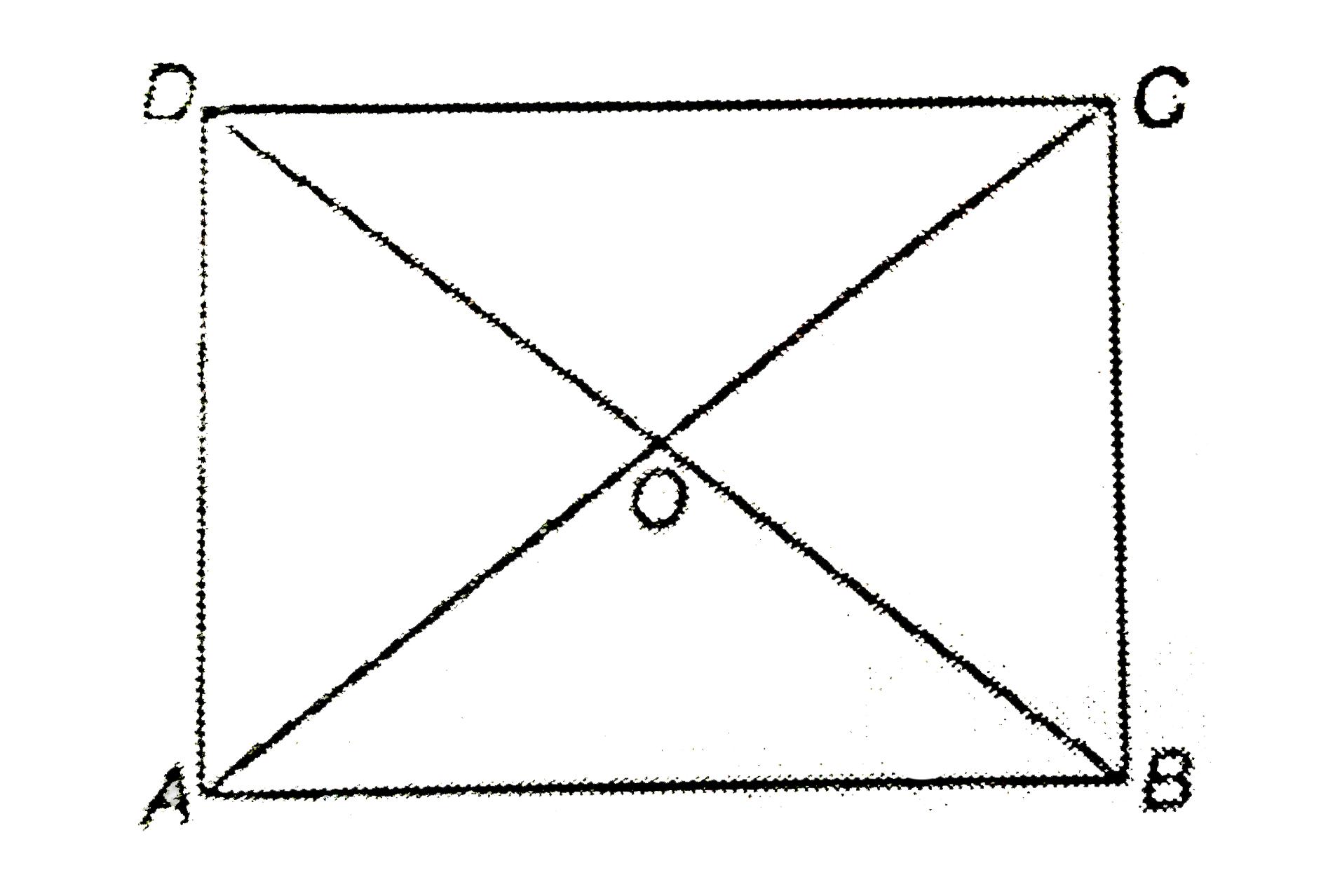
ABCD is a rectangle if ∠BPC = 124°Calculate : i ∠BAP ii ∠ADP
Diagonals of rectangle are equal and bisect each other.
Related Solutions

ABCD is a rectangle.
If .
Calculate:
(i)
(ii) .
View Solutionआकृति में, ABCD एक समांतर चतुर्भुज है,जिसमें तथा तो तथा का मान ज्ञात करें।
View SolutionFind the ABCD rectangle 7 cm on the map and the shaded area where the APD and BPC are semicircular. ( pi=3.14 Take that).
View SolutionWrite full name of (i) ADP (ii) ATP
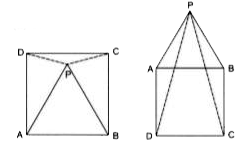
View SolutionIn the following diagrams, ABCD is a square and APB is an equilateral triangle. In each case,
(i) Prove that :
(ii) Find the angles of
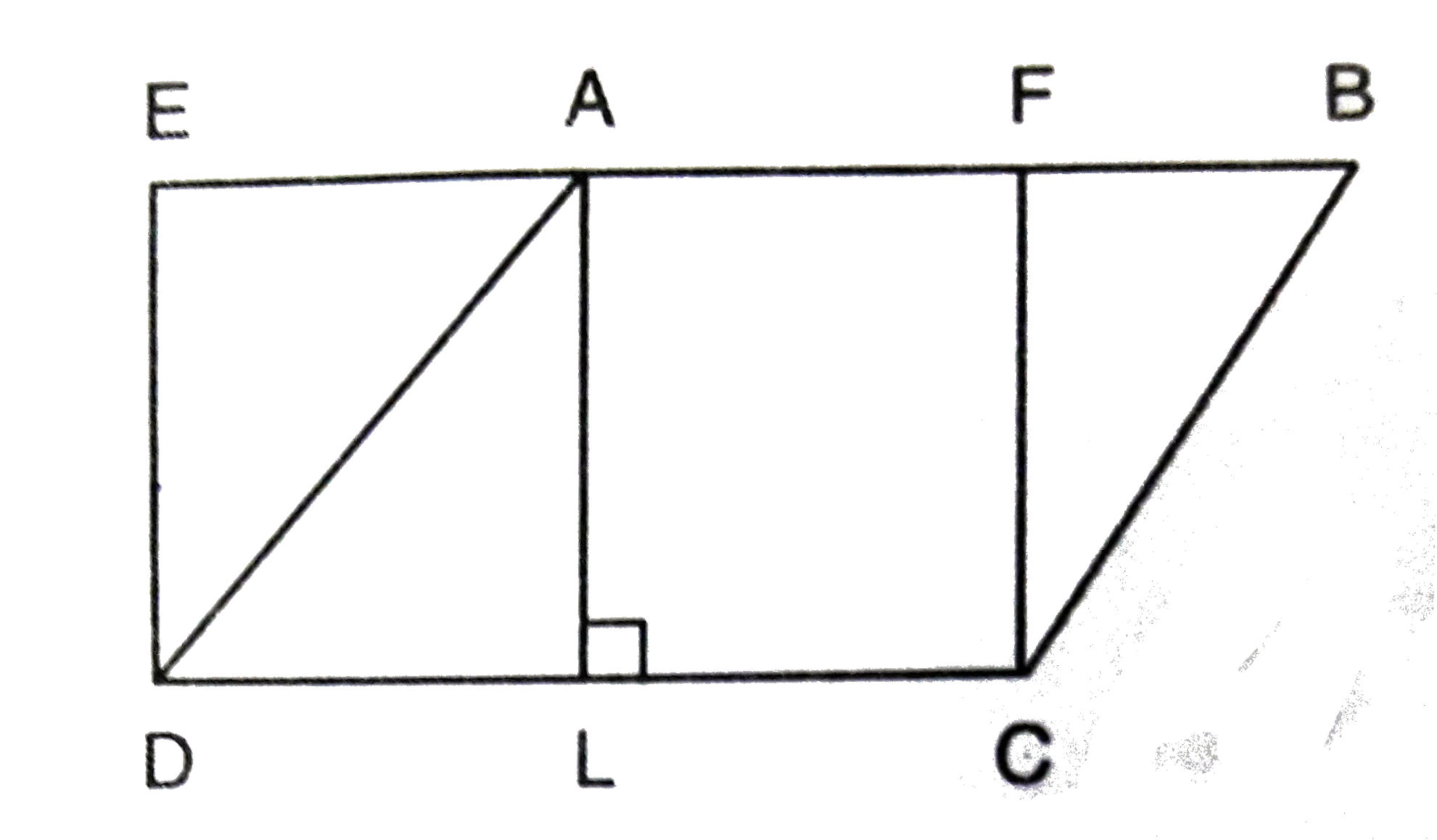
View SolutionABCD is parallelogram and ABEF is a rectangle and DG is perpendicular on AB.
Prove that (i) ar (ABCD) = ar(ABEF)
(ii) ar (ABCD) =
View Solutionचित्र में , ABCD एक समान्तर चतुर्भुज है तथा EFCD एक आयत है। साथ ही , तो सिद्ध कीजिए कि
View SolutionABCD is parallelogram and ABEF is a rectangle and DG is perpendicular on AB.
Prove that (i) ar (ABCD) = ar(ABEF)
(ii) ar (ABCD) =
View SolutionABCD is parallelogram and ABEF is a rectangle and DG is perpendicular on AB.
Prove that (i) ar (ABCD) = ar(ABEF)
(ii) ar (ABCD) =
View SolutionABCD is parallelogram and ABEF is a rectangle and DG is perpendicular on AB.
Prove that (i) ar (ABCD) = ar(ABEF)
(ii) ar (ABCD) =
View Solutionआक्रति 9.13 में , ABCD एक समांतर चतुर्भुज है और EFCD एक आयत है ।
साथ ही , है सिद्ध कीजिए कि
(i)
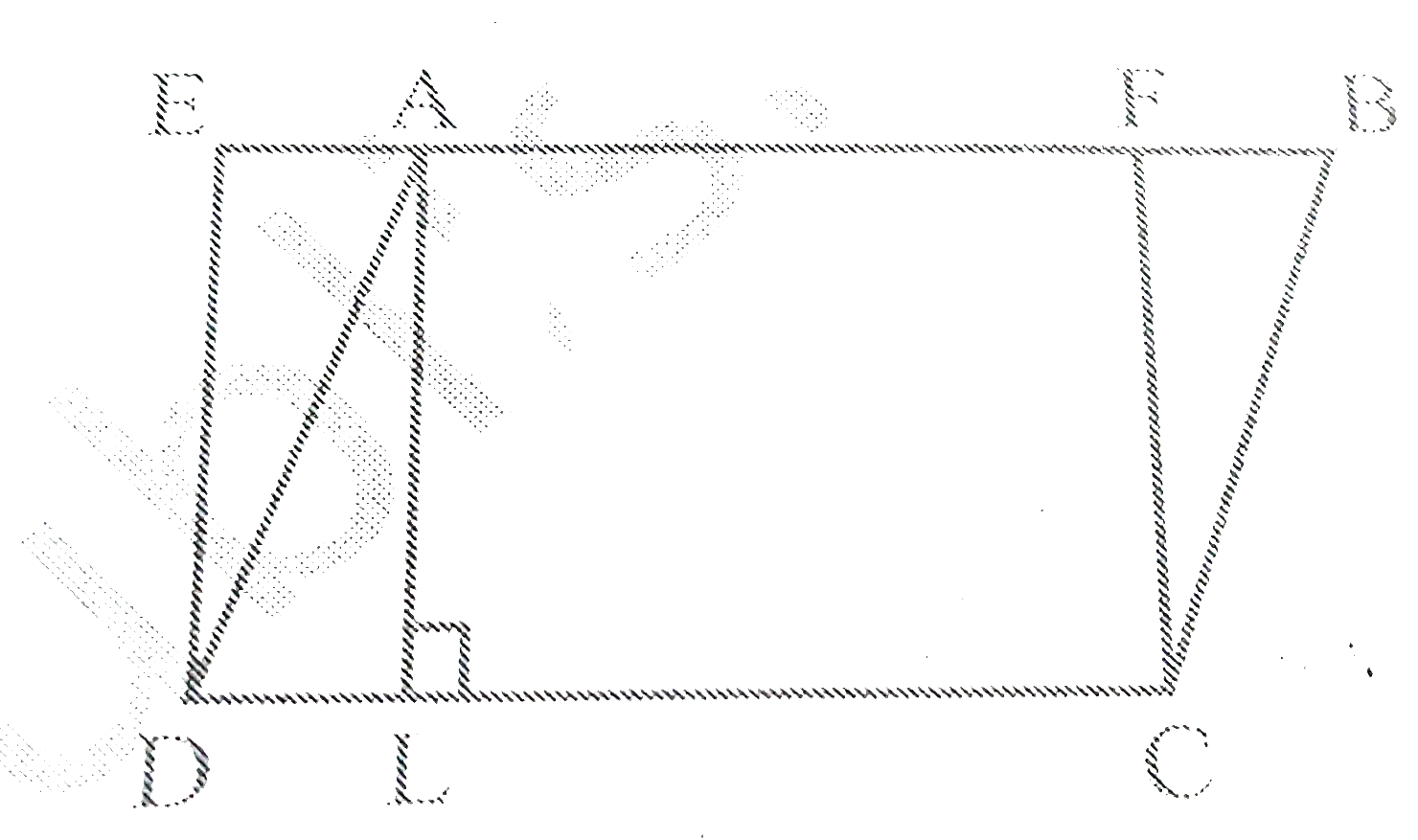
View SolutionABCD is a rectangle (Fig. 11.31) in which DP and BQ are perpendiculars from D and B respectively on diagonal AC. Show that(1) Delta ADP = Delta ACBQ (ii) /_ADP = /_CBQ(iii) DP = BQ
View SolutionIn given fig ABCD is a rectangle Calculate the area of shaded portion.
View SolutionIn a rectangle , . Calculate side .
View SolutionABCD is a rectangle in which diagonal AC bisects as well as Show that
(i) ABCD is a square
(ii) diagonal AD bisects
View SolutionABCD is a rectangle in which diagonal AC bisects as well as Show that
(i) ABCD is a square
(ii) diagonal BD bisects

View SolutionABCD is a rectangle in which diagonal AC bisects /_C. Show that ABCD is a square.
View SolutionABCD is a rectangle in which diagonal AC bisects as well as . Show that: (i) ABCD is a square (ii) diagonal BD bisects as well as .
View SolutionABCD is a rectangle in which diagonal AC bisects as well as . Show that:
(i) ABCD is a square
(ii) diagonal BD bisects as well as .
View SolutionABCD is a rectangle in which diagonal AC bisects as well as . Show that:(i) ABCD is a square (ii) diagonal BD bisects as well as .
View Solution