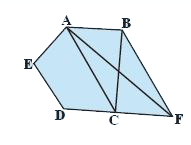
चित्र में , ABCD एक समान्तर चतुर्भुज है तथा EFCD एक आयत है। साथ ही AL⊥DC, तो सिद्ध कीजिए कि
(i)ar(ABCD)=ar(EFCD)
(ii)ar(ABCD)=DC×AL
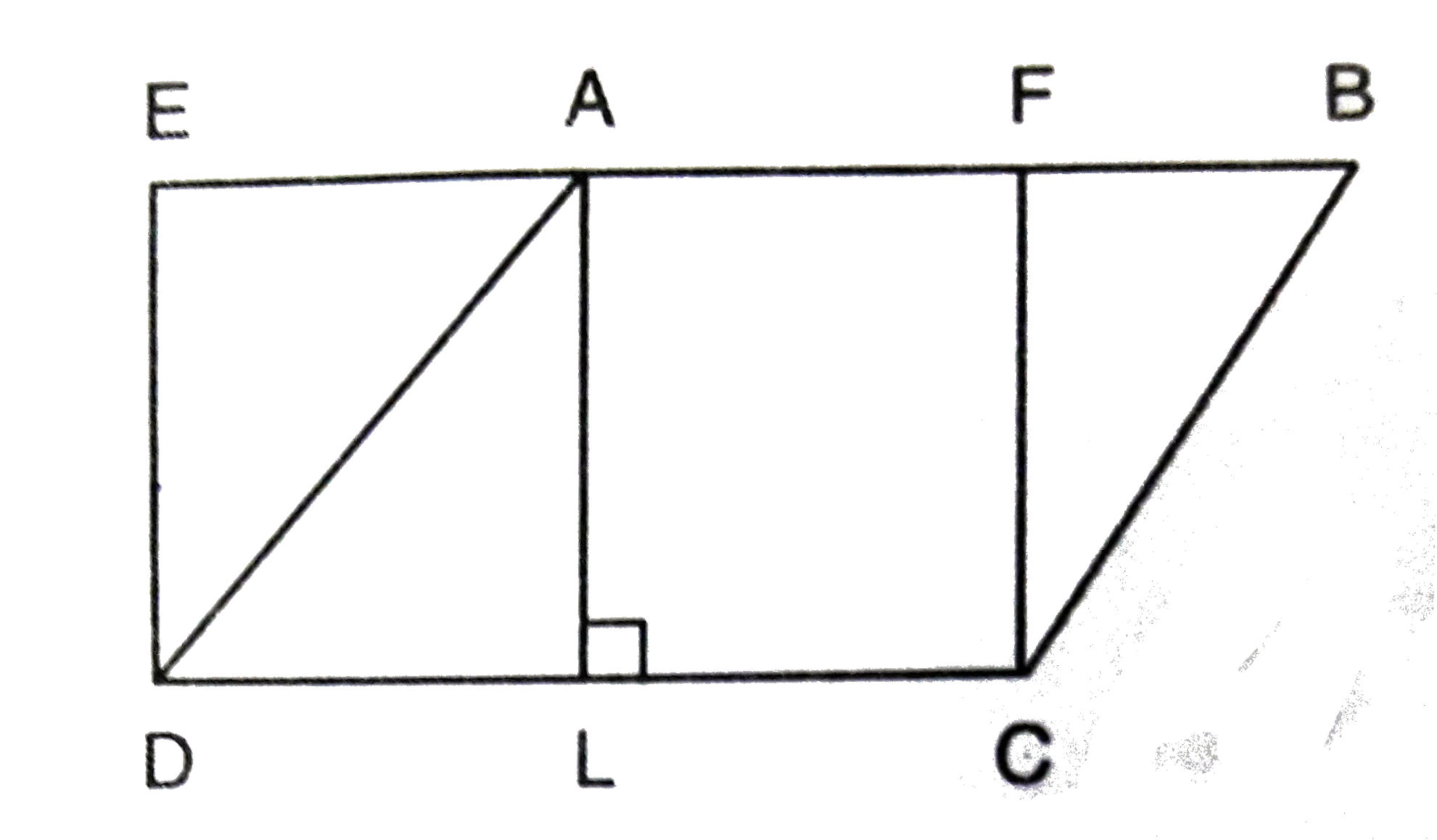

(i)हम जानते है कि आयत भी एक समान्तर चतुर्भुज है।
अतः समान्तर चतुर्भुज ABCD तथा आयत EFCD एक ही आधार CD तथा समान समांतर रेखाओं CD तथा BE के बीच में स्थित है।
∴ar(ABCD)=ar(EFCD)
(ii) चूंकि ar(ABCD)=ar(EFCD)
⇒ar(ABCD)=CD×FC
[∴ आयत का क्षेत्रफल =आधार × ऊँचाई ]
⇒ar(ABCD)=CD×AL
[ चूंकि AL=FC क्योंकि ALCF एक आयत है ]
⇒ar(ABCD)=DC×AL
Topper's Solved these Questions
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Book:RD SHARMAChapter:समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Exercise:व्याख्यात्मक उदाहरण
Explore 1 Video
- समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Book:RD SHARMAChapter:समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल Exercise:प्रश्नावली 15.1
Explore 6 Videos
- संख्यिकीय आंकड़ों का आलेखीय निरूपण Book:RD SHARMAChapter:संख्यिकीय आंकड़ों का आलेखीय निरूपण Exercise:बहु विकल्पीय प्रश्न
Explore 8 Videos
- सर्वांगसम त्रिभुजेंBook:RD SHARMAChapter:सर्वांगसम त्रिभुजेंExercise:बहु विकल्पीय प्रश्न
Explore 17 Videos
Similar Questions
चित्र में , P समान्तर चतुर्भुज ABCD के अभ्यन्तर में स्थित कोई बिंदु है दर्शाइए कि
(i) ar(ΔAPB)+ar(ΔPCD)=12ar(।।gmABCD)
(ii) ar(ΔAPD)+ar(ΔPBC)=ar(ΔAPB)+ar(ΔPCD)

View Solutionआकृति में आकृति एक ही आधार तथा समान समांतर रेखाओं के बीच स्थित है :

View Solutionनिम्न में से कौन - सा , सांख्यिकीय आकड़ो का लेखा चित्रीय निरूपण नहीं है ?
View Solutionयदि ΔABC≅ΔLKMहों, तो ΔLKMकी कौन सी भुजा ΔABCकी भुजा BC के एक बराबर होगी ?
View SolutionABCD is a trapezium in which AB |DC,AB=16cm and DC=24cm. If E and Fare respectively the midpoints of AD and BC prove that ar(ABFE)=(9)/(11)ar(EFCD)
View SolutionMatch the following Column A to Column B

View Solutionआक्रति 9.13 में , ABCD एक समांतर चतुर्भुज है और EFCD एक आयत है ।
साथ ही , AL⊥DC है सिद्ध कीजिए कि
(i) ar(ABCD)=ar(EFCD)
(ii)(ABCD)=DC×AL
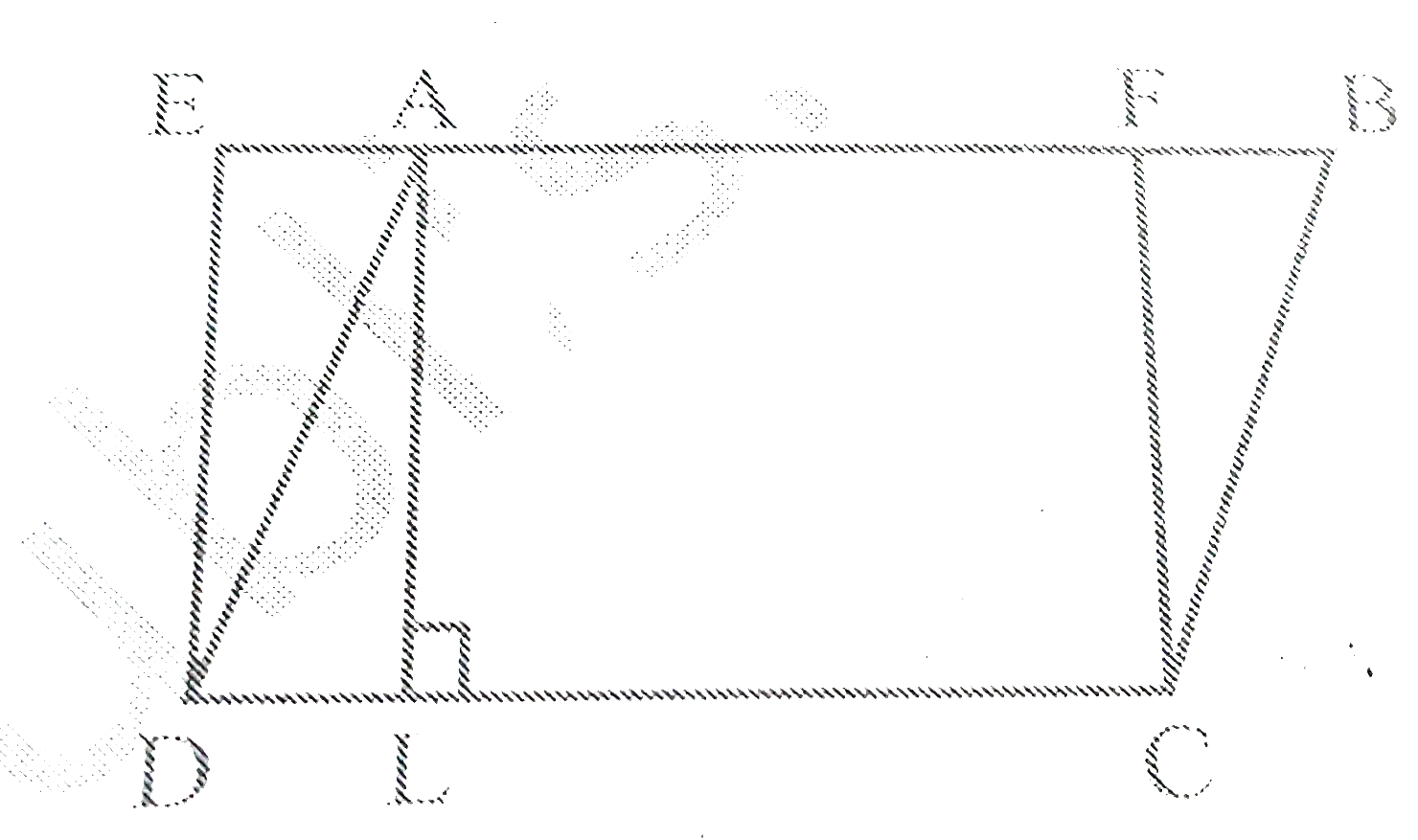
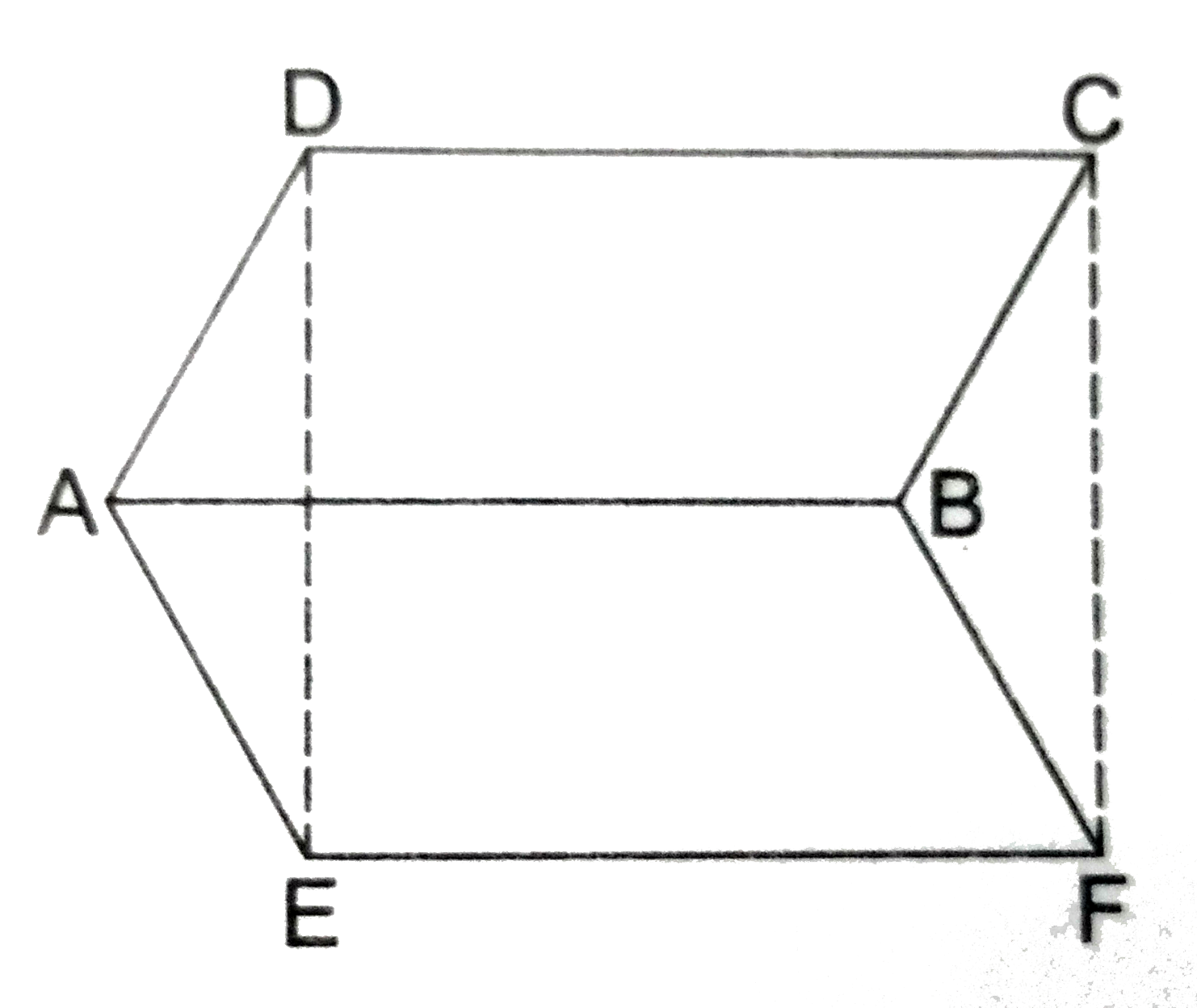
View SolutionIn the adjoing figure, two parallelograms ABCD and AEFB are drawn on opposite sides of AB. Prove that
ar(||gm ABCD)+ar(||gm AEFB)
=ar(||gm EFCD).
View Solutionयदि ABCD एक समांतर चतुर्भुज है, तो सिद्ध कीजिए कि
ar(ΔABD)=ar(ΔBCD)=ar(ΔABC)=ar(ΔACD)=12ar(||gmABCD)
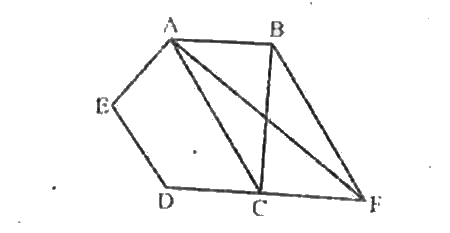
View SolutionIn, ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F. Show that
(i)ar (ACB) = ar (ACF)
(ii)ar (AEDF) = ar(ABCDE)
View SolutionABCD is parallelogram and ABEF is a rectangle and DG is perpendicular on AB.
Prove that (i) ar (ABCD) = ar(ABEF)
(ii) ar (ABCD) = AB×DG
View SolutionIn the figure, ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F. Show that
(i) ar(ΔACB)=ar(ΔACF)
(ii) ar(AEDF)=ar(ABCDE)
View SolutionABCD is parallelogram and ABEF is a rectangle and DG is perpendicular on AB.
Prove that (i) ar (ABCD) = ar(ABEF)
(ii) ar (ABCD) = AB×DG
View SolutionABCD is parallelogram and ABEF is a rectangle and DG is perpendicular on AB.
Prove that (i) ar (ABCD) = ar(ABEF)
(ii) ar (ABCD) = AB×DG
View SolutionABCD is parallelogram and ABEF is a rectangle and DG is perpendicular on AB.
Prove that (i) ar (ABCD) = ar(ABEF)
(ii) ar (ABCD) = AB×DG
View Solution

