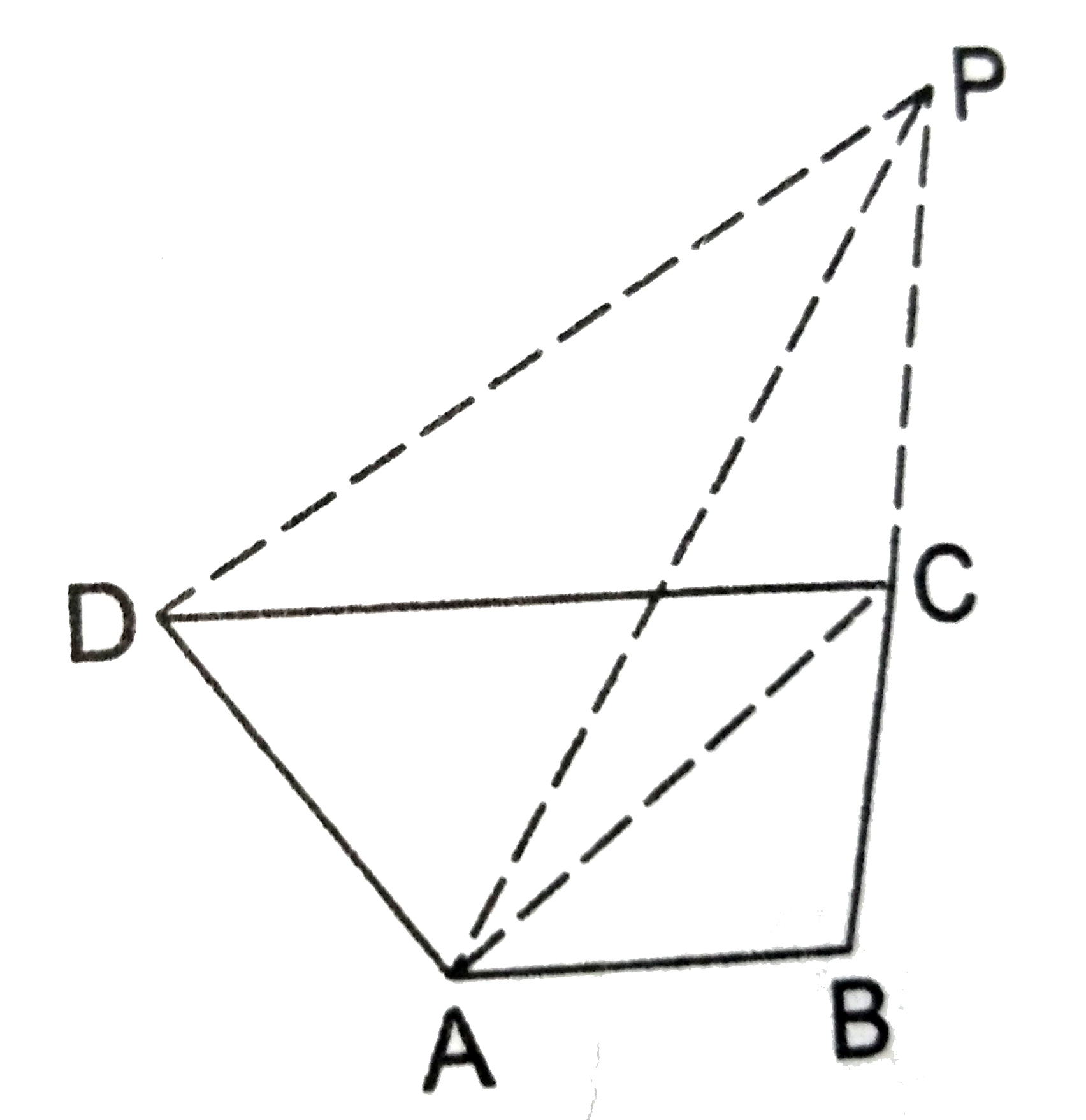
The side AB of a parallelogram ABCD is produced to any point P. A line through A and parallel to CP meets CB produced at Q and then parallelogram PBQR is completed see the following figure. Show that ar ABCD = ar PBQR. [Hint: Join AC and PQ. Now compare area ACQ and area APQ]
Let us join AC and PQ.ΔACQ and ΔAQP are on the same base AQ and between the same parallels AQ and CP.⊥ Area ΔACQ = Area ΔAPQ⊥ Area ΔACQ − Area ΔABQ = Area ΔAPQ − Area ΔABQ⊥ Area ΔABC = Area ΔQBP ... 1Since AC and PQ are diagonals of parallelograms ABCD and PBQR respectively ⊥ AreaΔABC = 1/2 Area ABCD ... 2Area ΔQBP = 1/2 Area PBQR ... 3From equations 1 2 and 3 we obtainArea ABCD = 1/2 Area PBQRArea ABCD = 1/2 Area PBQR
Related Solutions
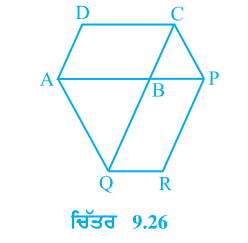
ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ ABCD ਦੀ ਇੱਕ ਭੁਜਾ AB ਨੂੰ ਇੱਕ ਬਿੰਦੂ P ਤੱਕ ਵਧਾਇਆ ਗਿਆ ਹੈ। A ਵਿੱਚੋਂ ਲੰਘਦੀ CP ਦੇ ਸਮਾਂਤਰ ਖਿੱਚੀ ਗਈ ਰੇਖ, ਵਧਾਈ ਹੋਈ CB ਨੂੰ Q 'ਤੇ ਮਿਲਦੀ ਹੈ ਅਤੇ ਫਿਰ ਸਮਾਂਤਰ ਚਤੁਰਭੁਜ PBQR ਨੂੰ ਪੂਰਾ ਕੀਤਾ ਗਿਆ ਹੈ।(ਦੇਖੋ ਚਿੱਤਰ 9.26)। ਦਰਸਾਓ ਕਿ ar (ABCD) = ar (PBQR) ਹੈ। [ਸੰਕੇਤ: AC ਅਤੇ PQ ਨੂੰ ਮਿਲਾਓ। ਹੁਣ ar (ACQ) ਅਤੇ ar (APQ) ਦੀ ਤੁਲਨਾ ਕਰੋ।]
View SolutionThe side AB of a parallelogram ABCD is produced to any point P. A line through A and parallel to CP meets CB produced at Q and then parallelogram PBQR is completed as shown in Figure. Show that
View SolutionThe side AB of a parallelogram ABCD is produced to any point P. A line through A and parallel to CP meets CB produced at Q and then parallelogram PBQR is completed as shown in Figure. Show that
View SolutionThe side AB of a parallelogram ABCD is produced to any point P. A line through A and parallel to CP meets CB produced at Q and then parallelogram PBQR is completed . Show that ar (ABCD) = ar (PBQR)
View SolutionThe sides AB of parallelogram ABCD produced to any point P. A line through A and parallel to CP meets CB produced at Q and the parallelogram PBQR is completed Show that ar(ABCD) = ar(PBQR)
View Solutionसमांतर चतुर्भुज ABCD की एक भुजा AB को एक बिंदु P तक बढ़ाया गया है । A से होकर CP के समांतर खींची गई रेखा बढ़ाई गई CB को Q पर मिलती है और फिर समांतर चतुर्भुज PBQR को पूरा किया गया है ( देखिए आक्रति 9.26 )| दर्शाइए कि
है |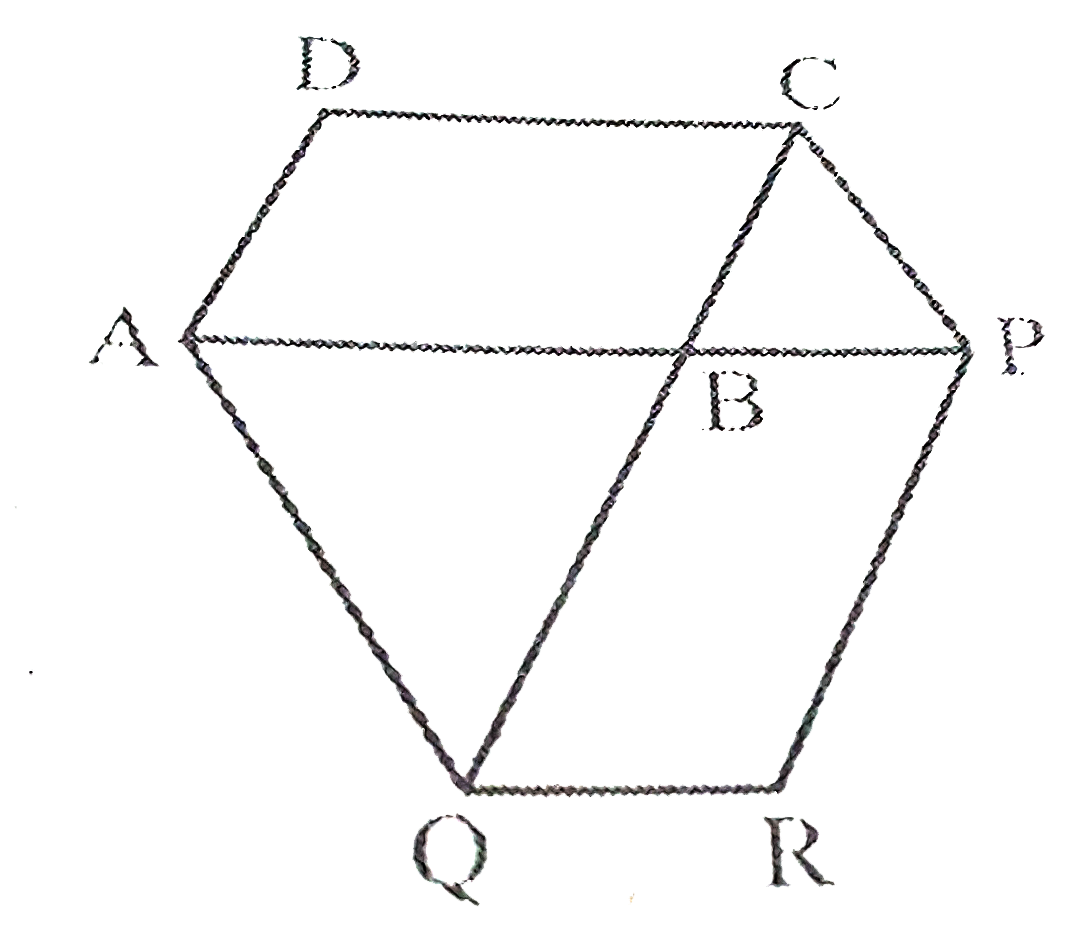
View Solutionसमांतर चतुर्भुज ABCD की भुजा AB को किसी बिंदु P तक बढ़ाया गया है। बिंदु A से CP के समांतर खींची गयी रेखा CB के आगे बढ़ाये गये भाग को Q पर मिलती है। और समांतर चतुर्भुज PBQR को पूरा करती है। सिद्ध कीजिए कि
View Solutionसमांतर चतुर्भुज ABCD की एक भुजा AB को एक बिन्दु P तक बढ़ाया गया है। A से होकर CP के समांतर खींची गई रेखा बढ़ाई गई CB को Q पर मिलती है और फिर समांतर चतुर्भुज PBQP को पूरा किया गया है (देखिए आकृति )। दर्शाइए कि (ABCD ) = क्षेत्रफल (PBQR ) है।

View SolutionA side AB of a parallelogram ABCD is produced to a point P. A line drawn parallel to CP through A meets the produced CB at Q and then the parallelogram PBOR is completed.
View SolutionThe side AB of a parallelogram ABCD is produced to any point E. A line through A and parallel to CE meets CB produced at G and then parallelogram EBGF is completed (see the figure). Prove that
area of .
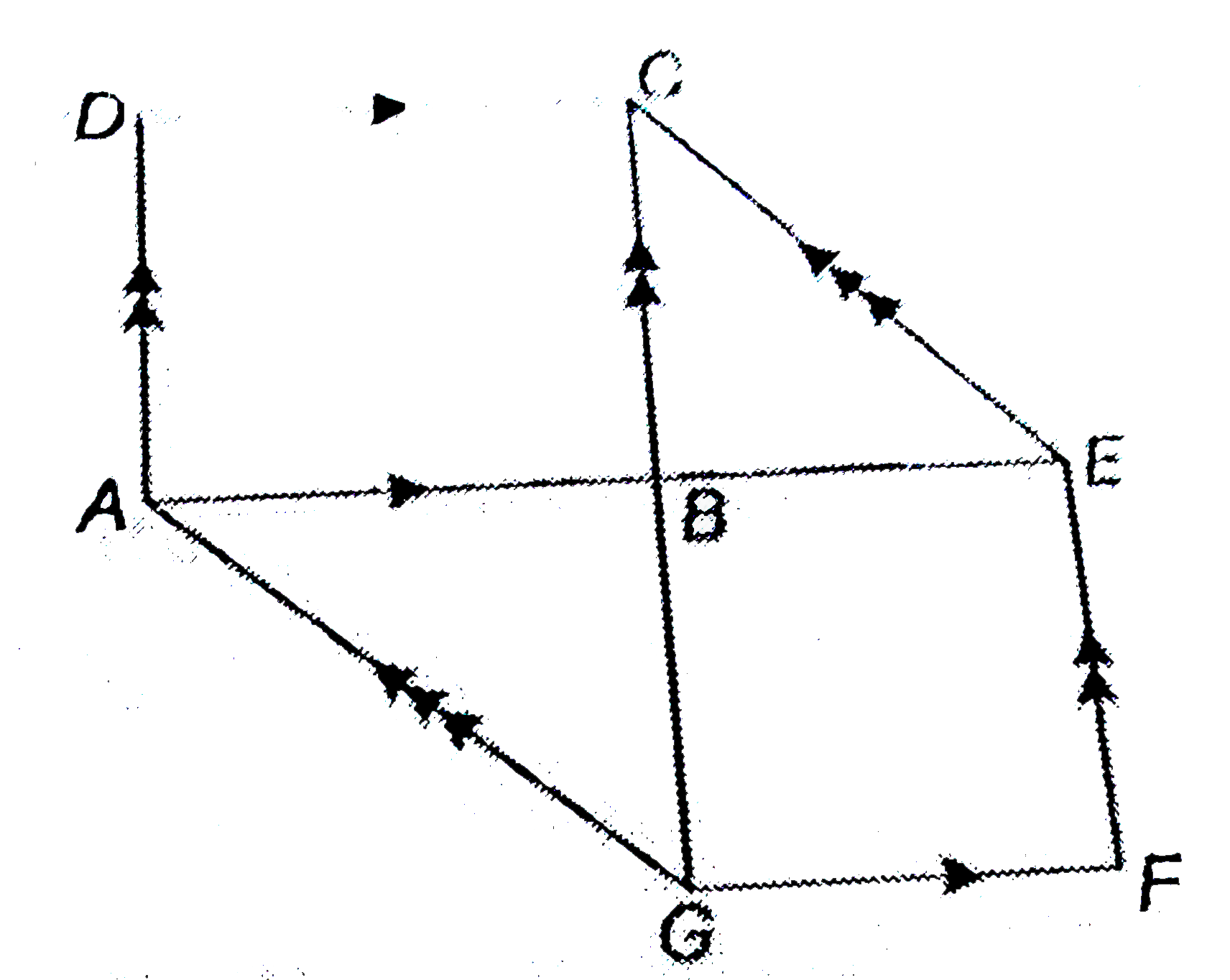
View SolutionThe side AB of a parallelogram ABCD is produced to any point P. A line through A and parallel to CP meets CB produced at Q and then parallelogram PBQR is completed. Show that
View SolutionThe side AB of a parallelogram ABCD is produced to any point P. A line through A and parallel to CP meets CB produced at Q and then parallelogram PBQR is completed. Show that .
View SolutionIn the figure ABCDE is any pentagon. BP drawn parallel to AC meets DC produced at P and EQ drawn parallel to AD meets CD produced at Q. Prove that : ar(ABCDE) = ar(APQ)
View SolutionABCD is a parallelogram and a line through A meets DC at P and BC (produced) at Q. Prove that ar(triangleBPC) = ar(triangleDPQ)
View SolutionABCDE is a pentagon. A line through B parallel to AC meets DC produced at F. Show that: ar(AEDF) = ar(ABCDE)
View SolutionIn the parallelogram , the line drawn through point on , parallel to meets at . The line through , parallel to meets .
Prove that
. .
.
View SolutionIn the figure,ABCD is a parallelogram and PQR is a rectangle.If AP:PB=1:2=PD:DR, what is the ratio of the area of ABCD to the area of PBQR?
View SolutionIn the figure, ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F. Show that ar( Delta AEDF) = ar( Delta ABCDE)
View SolutionIn the given figure, ABCDE is a pentagon. A line drawn parallel to AC through B meets the produced DC at F. show that ar( AEDF) = ar ( ABCDE)
View SolutionIn the adjoining figure, ABCD is a quadrilateral. A line through D, parallel to AC, meets BC produced in P .
Prove that .
View Solution