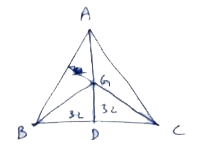
If AD is a median of a triangle ABC then prove that triangles ADB and ADC are equal in area. If G is the mid-point of median AD prove that ar ∆ BGC = 2 ar ∆ AGC.
To prove that ar ∆ BGC = 2 ar ∆ AGC
Related Solutions
यदि त्रिभुज ABC की AD एक माध्यिका है, तो सिद्ध करो कि त्रिभुज ADB और त्रिभुज ADC का क्षेत्रफल बराबर है । यदि माध्यिका AD का मध्य बिंदु G हो, तो सिद्ध करो कि
है।
View SolutionIf the medians of a triangle ABC meet at G, prove that ar (AGB) = ar (AGC) = ar (BGC) = (1)/(3) is ar (ABC).
View SolutionIn a is median, G is a Mid point of AD. If area of IS 32 SQ . units then find area of
View SolutionABC एक त्रिभुज है तथा इसकी एक माध्यिका है यदि पर कोई बिंदु है तब सिद्ध कीजिए कि
View SolutionIf the median of a △ABC intersect at G. show that ar (△AGC) = ar (△AGB) = ar (△BGC) = 1/3 ar (△ABC)
View SolutionDelta ABC The medians of AD,BE and CF intersect at G. prove that the area Delta AGB = Area Delta AGC= Area Delta BGC = ( 1)/( 3) Area Delta ABC
View SolutionIf the medians of a triangleABC intersect at G, show that ar(AGB) = ar(AGC) = ar(BGC) = 1/3 ar(ABC)
View SolutionIf the medians of a triangleABC intersect at G, show that ar(AGB) = ar(AGC) = ar(BGC) = 1/3 ar(ABC)
View SolutionIn the given figure ar . AC is the median of . If ar (ACE) = ?
View SolutionIn a triangle ABC, E is the mid-point of median AD. Show that ar (BED) = ar (ABC).
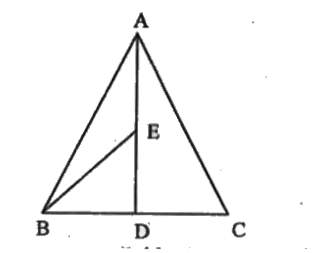
View SolutionIn a triangle ABC, E is the mid - point of median AD. Show that ar (BED) =1/4 ar (ABC)
View SolutionE is any point on median AD of a . Show that ar (ABE) = ar (ACE).
View SolutionDelta ABC In BC, if D is the mid-point of the side BC and E is the mid-point of the median AD, then ar( Delta BED) = ?
View Solutiontriangle In ABC, AD is the median. G is a point on AD such that AG: GD = 2:1 then ( triangle ABG): ar ( triangle ABC) will be equal to
View SolutionIn a triangle ABC, E is the mid-point of median AD. Show that ar (triangleBED)=1/4 ar( triangleABC ).
View SolutionIf P is a point on the median AD of a triangle ABC, then ar(ABP)near(ACP) is.
View SolutionIn the given figure, Delta ABC E is any point on the median of AD. show that ar (Delta ABE) = ar (DeltaACE)
View SolutionIn the given figure, Delta ABC E is any point on the median of AD. show that ar (Delta BED) = ar (DeltaCDE)
View Solutiontriangle In ABC, AD is the median and P is a point on AD such that AP: PD = 3:4, then ar ( triangle BPD) on ( triangle ABC) is equal to:
View SolutionAD is a median of triangle ABC. G is a mid point of AD. If area of triangle ABC is 16 sq. cm. Find the area of triangle GDC
View Solution