Figure shows only cross section a wooden cylinder C with a mass m of 0.25Kg. a radius R and a length l perpendicular to the plane of paper of 0.1 meter with N equal to 10 turns of wire wrapped around it longitudinally so that the plane of the wire loop contains the axis of cylinder. What is the least current through the loop that will prevent the cylinder from rolling down a plane whose surface is inclined at angle θ to the horizontal in the presence of a vertical field of magnetic induction 0.5 weber/meter2 if the plane of the windings is parallel to the inclined plane?
Related Solutions
Figure shows (only cross section) a wooden cylinder with a mass of ,a radius and a length perpenducular to the plane of paper of with where is number of turns of wire loop contains the axis of the cylinder the least current through the loop is that will prevent the cylinder from moving down a plane whose surface is inclined at angle to the horizontal, in the presence of a vertical field of magnetic induction , if the planer of the windings is parallel to the inclinded plane?(bottom most point of cylinder does not slip)then find value of .
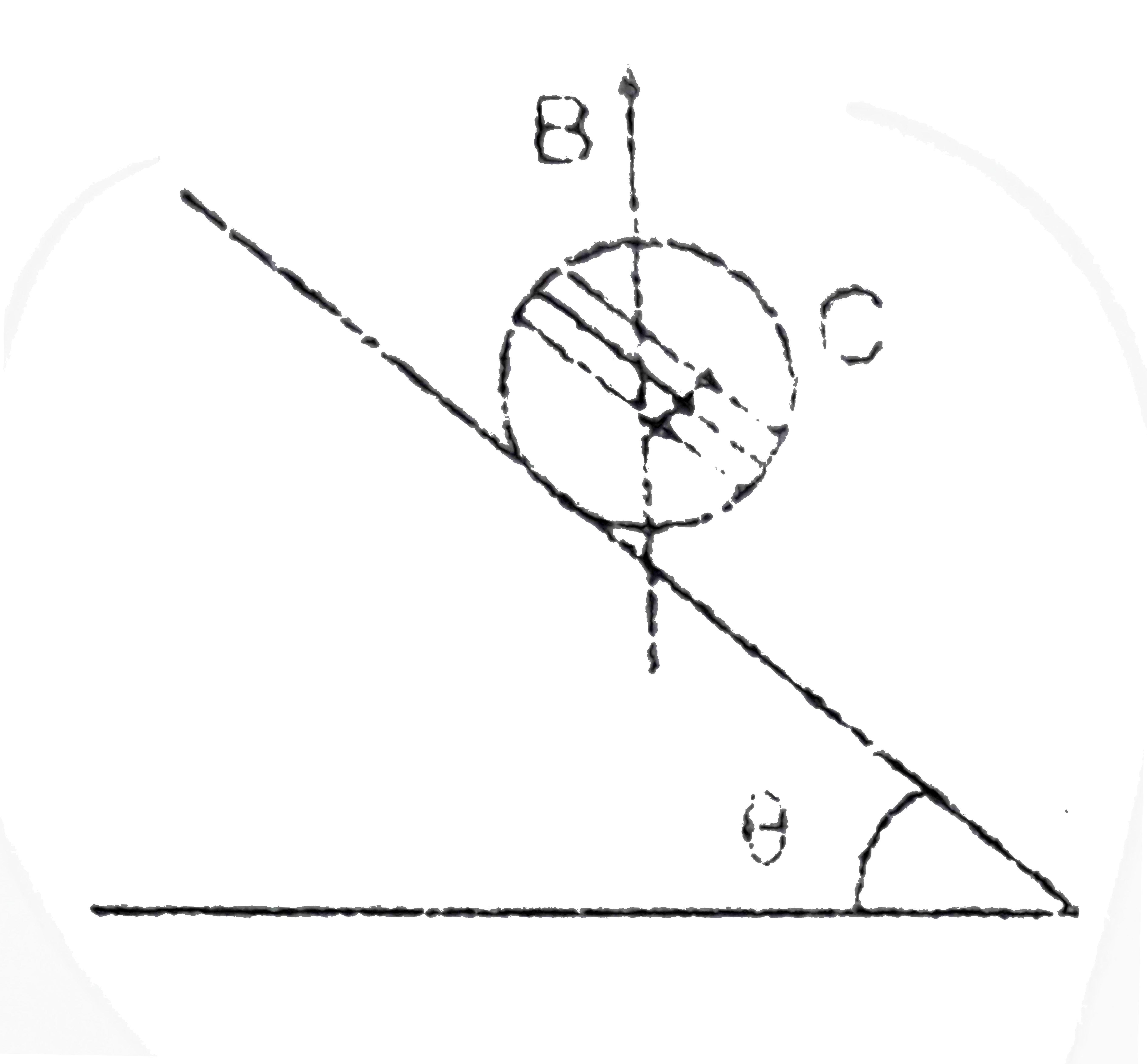
View SolutionFigure shows (only cross section) a wooden cylinder C with a mass m of 0.25 kg ,a radius R and a length l perpenducular to the plane of paper of 0.1 meter with N=10 where N is number of turns of wire loop contains the axis of the cylinder the least current through the loop is P/2A that will prevent the cylinder from moving down a plane whose surface is inclined at angle theta to the horizontal, in the presence of a vertical field of magnetic induction 0.5 weber//meter^(2) , if the planer of the windings is parallel to the inclinded plane?(bottom most point of cylinder does not slip)then find value of P .
View SolutionA circuit consists of a circular loop of radius R kept in the plane of paper and an infinitely long current carrying wire kept perpendicular to the plane of paper and passing through the centre of loop. The mutual inductance of wire and loop will be
View SolutionA circuit consists of a circular loop of radius R kept in the plane of paper and an infinitely long current carrying wire kept perpendicular to the plane of paper and passing through the centre of loop. The mutual inductance of wire and loop will be
View Solutionએક નિયમિત નળાકારની ત્રિજ્યા R અને લંબાઈ L છે. જો આ નળાકારના કેન્દ્રમાંથી પસાર થતી અને વર્તુળાકાર બાજુઓને લંબ એવી અક્ષને અનુલક્ષીને નળાકારની જડત્વની ચાકમાત્રા એ તે જ નળાકારના કેન્દ્રમાંથી પસાર થતી અને તેની લંબાઈને લંબ એવી અક્ષને અનુલક્ષીને નળાકારની જડત્વની ચાકમાત્રા જેટલી હોય, તો નળાકારની લંબાઈ (L) અને ત્રિજ્યા (R) નો ગુણોત્તર શોધો.
View SolutionA long cylinder of uniform cross section and radius R is carrying a current i along its length and current density is uniform cross section and radius r in the cylinder parallel to its length. The axis of the cylinderical cavity is separated by a distance d from the axis of the cylinder. Find the magnetic field at the axis of cylinder.
View SolutionA long cylinder of uniform cross section and radius R is carrying a current i along its length and current density is uniform cross section and radius r in the cylinder parallel to its length. The axis of the cylinderical cavity is separated by a distance d from the axis of the cylinder. Find the magnetic field at the axis of cylinder.
View SolutionFigure shows a long straight wire carrying current I and a square conducting wire loop of side l, at a distance 'a' from current wire. Both the current wire and loop are in the plane of paper. Find the flux of magnetic filed of current wire, passing through the loop.
View SolutionWhat is moment of inertia of a solid cylinder of mass , length l and radius about the axis of the cylinder ?
View SolutionElectric current is passing unfiormly through a solid cylinderical wire of radius R. The current I passing through circular cross-section of radius r measured from the axis of the cylinder (r lt R ) varies as shown in
View SolutionElectric current is passing unfiormly through a solid cylinderical wire of radius R. The current I passing through circular cross-section of radius r measured from the axis of the cylinder (r lt R ) varies as shown in
View SolutionThe figure shows a long cylinder and its cross section. There are N (N is a large number) wire on the curved surface of the cylinder at uniform spacing and paral- lel to its axis. Each wire has current I and cross sectional radius of wires are small compared to radius R of the cyl- inder. Find magnetic field at a distance x from the axis of the cylinder for (b)

View SolutionA long straight wire carrying current I and a square conducting wire loop of side l , at a distance 'a' from current wire as shown in the figure. Both the current wire and loop are in the plane of paper. Find the magnetic flux of current wire, passing through the loop.
View SolutionIn the figure, a long straight wire carrying a current and a loop of a square conducting wire of side l are located at a distance 'a' from the current carrying wire, both the current carrying wire and the loop are in the plane of the paper, find the magnetic flux of the current carrying wire passing through the loop Do it
View SolutionFigure shows a long straight wire carrying current , and a square conducting wire loop of side i, at a distance 'a' from current wire. Both the current wire and loop arc in the plane of paper. Find the flux of magnetic field of current wire, passing through the loop.
View SolutionA cylinder of mass m and radius R rolls down an inclined plane of inclination theta . Calculate the linear acceleration of the axis of cylinder.
View SolutionA cylinder of mass m and radius R rolls down an inclined plane of inclination theta . Calculate the linear acceleration of the axis of cylinder.
View SolutionThe figure shows an infinitely long current wire out of the plane of the paper ( shown as a dot ). A current carrying loop ABCD is placed as shown in figure. The loop

View SolutionThe moment of inertia of a solid cylinder of mass M, length 2 R and radius about R an axis passing through the centre of mass and perpendicular to the axis of the cylinder is I and about an axis passing through one end of the cylinder and perpendicular to the axis of cylinder is ,then
View SolutionThe moment of inertia of a solid cylinder of mass M, length 2 R and radius R about an axis passing through the centre of mass and perpendicular to the axis of the cylinder is I, and about an axis passing through one end of the cylinder and perpendicular to the axis of cylinder is I_2 then
View Solution