In the given below fig rays OA OB OC OP and OE have the common end point O. Show that ∠AOB + ∠BOC + ∠COD + ∠DOE + ∠EOA = 360°.
Given that Rays OA OB OD and OE have the common end point O. A ray of opposite to OA is drawnBy adding 1 and 2 equations we get ∠AOB + ∠BOC + ∠COF + ∠AOE + ∠DOF + ∠DOE = 360o ∠AOB + ∠BOC + ∠COD + ∠DOE + ∠EOA =360o Hence proved
Related Solutions
In given fig.
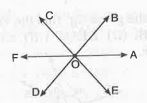
Rays OA, OB, OC, OD and OE have common initial point O. Show that .
View SolutionIn given fig.
 , Rays OA, OB, OC, OD and OE have common initial point O. Show that .
, Rays OA, OB, OC, OD and OE have common initial point O. Show that .
View Solution. Show that and
View Solutionकिरणें और OE का एक सर्वनिष्ठ अंत बिंदु है। दिखायें कि
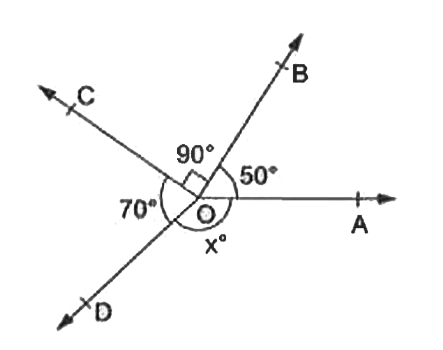
View SolutionIn the given figure, rays OA, OB, OC and OD are such that AOB = , BOC = , and . Then, the value of is
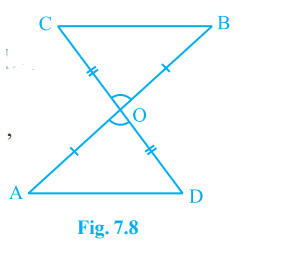
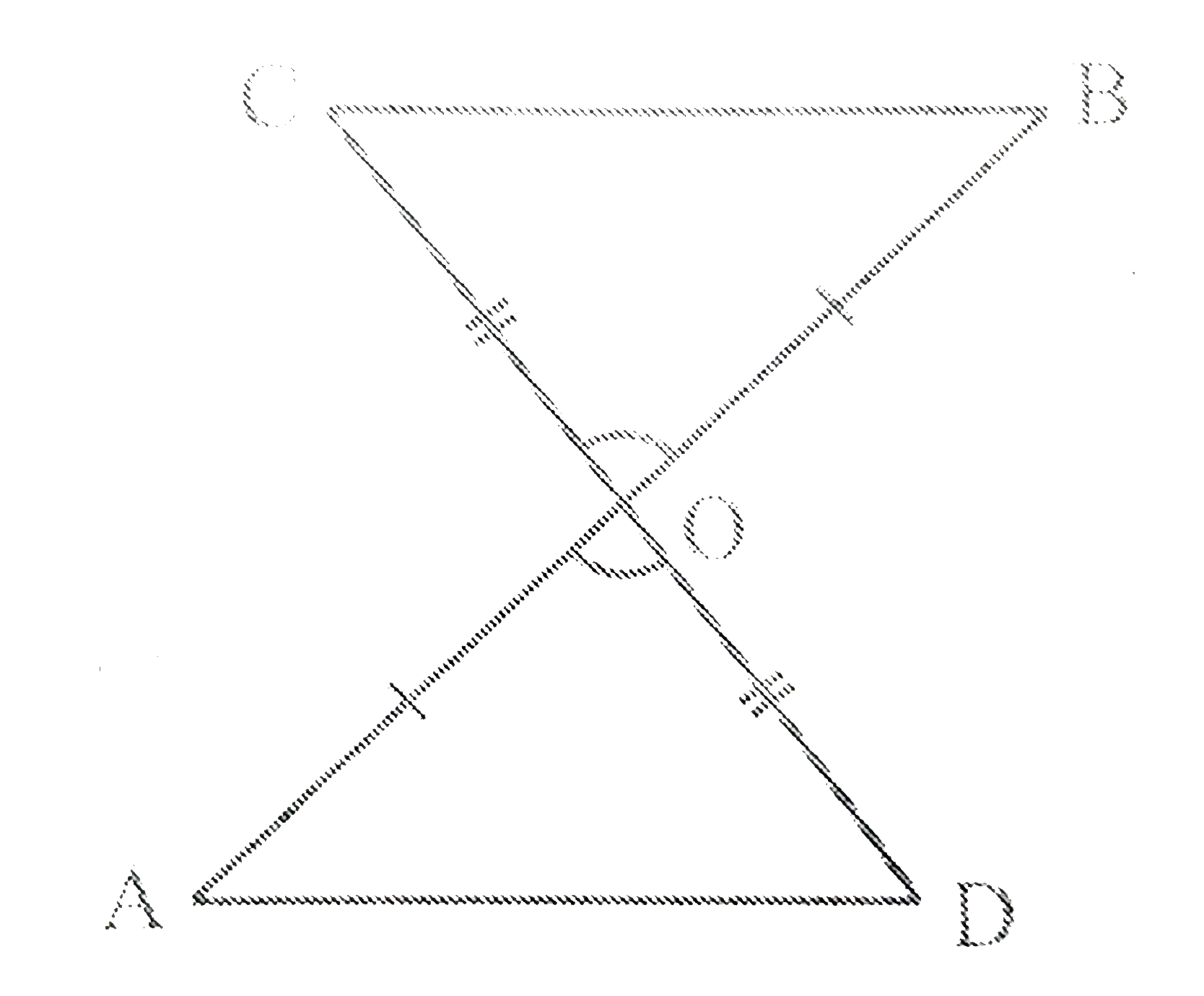
View SolutionIn Fig. 7.8, OA = OB and OD = OC. Show that (i) and (ii) AD || BC.
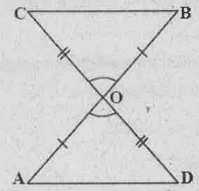
View SolutionIf AB and CD are intersecting at ‘O’, OA = OB and OD = OC. Show that triangle AOD ~= triangle BOC
View SolutionAB is a straight line and O is a point on AB, if a line OC is drawn not coinciding with OA or OB, then and are
View SolutionIn Fig. 2.54, o is a point in the interior of a triangle Show that
View SolutionABCD is a parallelogram and P the intersection of the diagonals, O is any point . Show that vec(OA)+vec(OB)+vec(OC)+vec(OD)=4vec(OP) .
View Solutionमाना कि O समष्टभुज ABCDEF का केंद्र हैं, तो
.
View SolutionLet O be the centre of a regular hexagon ABCDEF. Find the sum of the vectors , and
View Solutionif D,E and F are the mid-points of the sides BC,CA and AB respectively of the be any points, then prove that
View SolutionIf , and are the mid-points of the sides , and respectively of the and be any point, then prove that
View Solutionif D,E and F are the mid-points of the sides BC,CA and AB respectively of the be any points, then prove that
View SolutionIf , and are the mid-points of the sides , and respectively of the and be any point, then prove that
View Solutionआकृति में OA = OB और OD = OC है। दर्शाइए कि
(i) और (ii) AD || BC है।
View SolutionABCDEF is a regular hexagon. Show that : vec(OA)+vec(OB)+vec(OC)+vec(OD)+vec(OE)+vec(OF)=vec0 . Where O is the centre of the hexagon.
View SolutionIf E is the intersection point of diagonals of parallelogram ABCD and +++= where O is origin then
View Solutionఇచ్చిన పటంలో AB మరియు CD లు 'O' వద్ద ఖండించుకొనుచున్నాయి. OA=OB మరియు OD=OC అయిన
View Solution