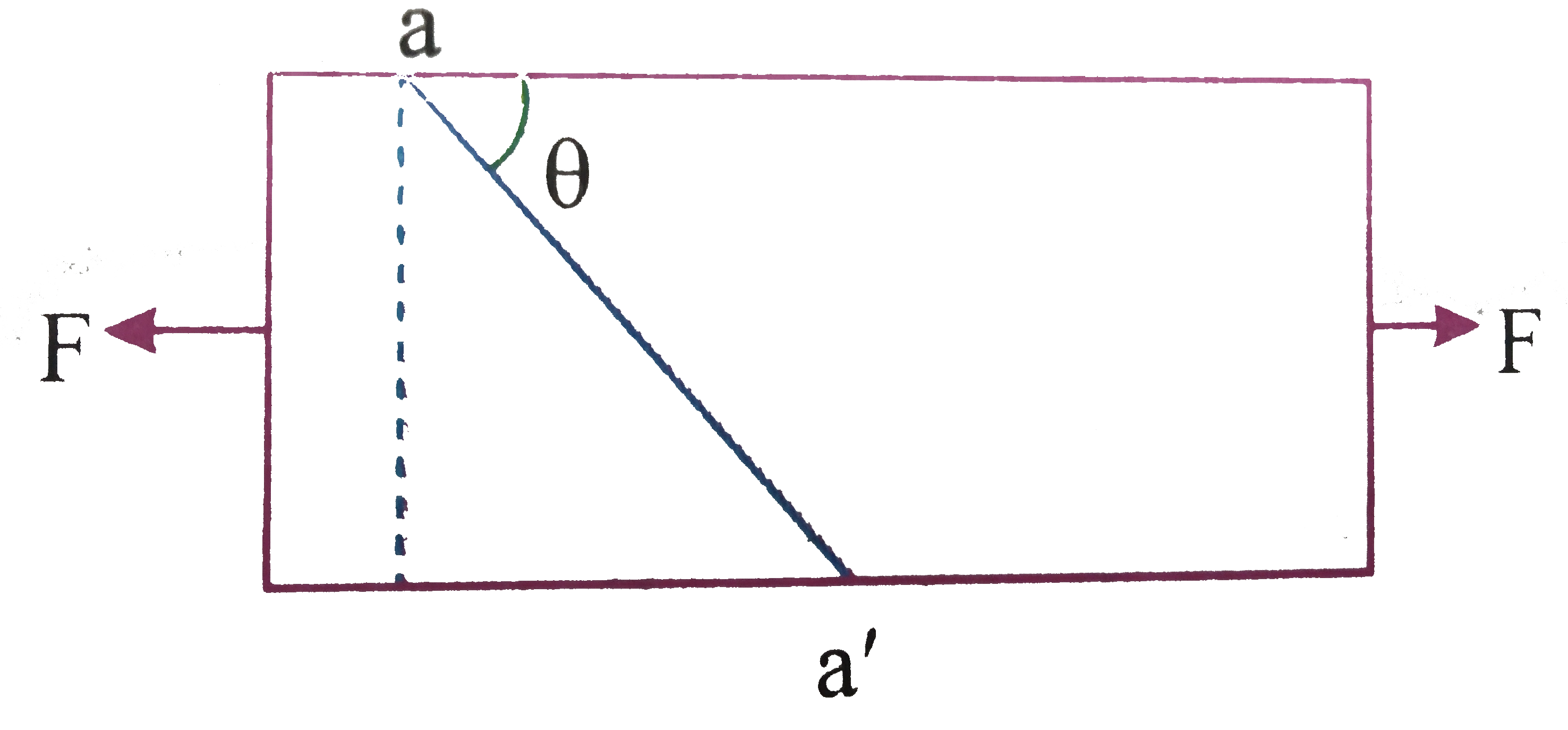
Consider a long steel bar under a tensile stress due to forces F acting at the edges along the length of the bar Fig. 9.5. Consider a plane making an angle θ with the length. What are the tensile and shearing stresses on this plane?a For what angle is the tensile stress a maximum?b For what angle is the shearing stress a maximum?
Let the cross sectional area of the bar be A. Consider the equilibrium of the plane aa . A force F must be acting on this plane making an angle π/2-θ with the normal ON. Resolving F into components along the plane and normal to the planeFp = F cosθFN = SinθLet the area of the face aa be A thenA/A = sinθA = A/SinθThe tensile stress T = Fsinθ/A = F/Asin2θ and the shearing stress Z = F cosθ/A = F/Acosθ sinθ = F sin2θ/2A. Maximum tensile stress is when θ = π/2 and maximum shearing stress when 2θ = π/2 or θ = π/4.
Related Solutions
Consider a long steel bar under a tensile stress due to force F acting at the edges along the length of the bar (as shown in figure). Consider a plane making an angle with the length. What are the tensile and shearing stresses on this plane? (a) For what angle is the tensile stress a maximum ? (b) For what angle is the shearing stress a maximum ?
View SolutionConsider a long steel bar under a tensile stress due to forces F, acting at the edges along the length of the bar Consider a plane making an angle theta with the length. What are the tensile and shering stresses on this plane ? (a) For what angle is the tensile stress a maximum ? (b) For what angle is the shearing stress a maximum ?
View SolutionConsider a long steel bar under a tensile stress due to forces F, acting at the edges along the length of the bar Consider a plane making an angle theta with the length. What are the tensile and shering stresses on this plane ? (a) For what angle is the tensile stress a maximum ? (b) For what angle is the shearing stress a maximum ?
View SolutionConsider a long steel bar under a tensile stress due to forces acting at the edge a along the length of the bar (show in the figure)
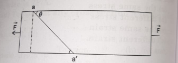
Consider a plane making an angle with the length. What are the tensile and shearing stresses on this plane?
For what angle is the shearing stress a maximum?
View SolutionConsider a long steel bar under a tensile stress due to forces acting at the edge a along the length of the bar (show in the figure)
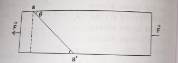
Consider a plane making an angle with the length. What are the tensile and shearing stresses on this plane?
For what angle is the tensile stress a maximum?
View SolutionConsider a long steel bar under a tensille due to force acting at the edges along the length of the bar (figure). Consider a plane making an angle with the length. For what angle is the tensile stress a maximum?
View SolutionA long steel bar is under a tensile stress due to a force F as shown. For what angle the tensile and shearing stress are maximum?

View Solutionस्टील की लंबी छड़ पर विचार कीजिए जिसके सिरों पर लंबाई के अनुदिश लगे बल Fके कारण तनन प्रतिबल है (चित्र 9.5)। एक ऐसे तल पर विचार कीजिए जो लंबाई से कोण बनाता है। इस तल पर तनन-प्रतिबल तथा अवरूपण-प्रतिबल क्या है?
(a) किस कोण के लिए तनन प्रतियल अधिकतम है?
(b) किस कोण के लिए अवरूपण प्रतिबल अधिकतम है?

View SolutionA long rod of steel under a tensile stress due to the force acting on the edges along the length. The value of angle 0 for which shearing stress is maximum is
View SolutionA bar of cross-section A is subjected to equal and opposite tensile forces F at its ends. Consider a plane through the bar making an angle with a plane at right angles to the bar. (a) What is the tensile stress at this plane in terms of F, A and @ ? (b) What is the shearing stress at the plane, in terms of F, A and (c) For what value of is the tensile stress a maximum? (d) For what value of is the shearing stress a maximum?

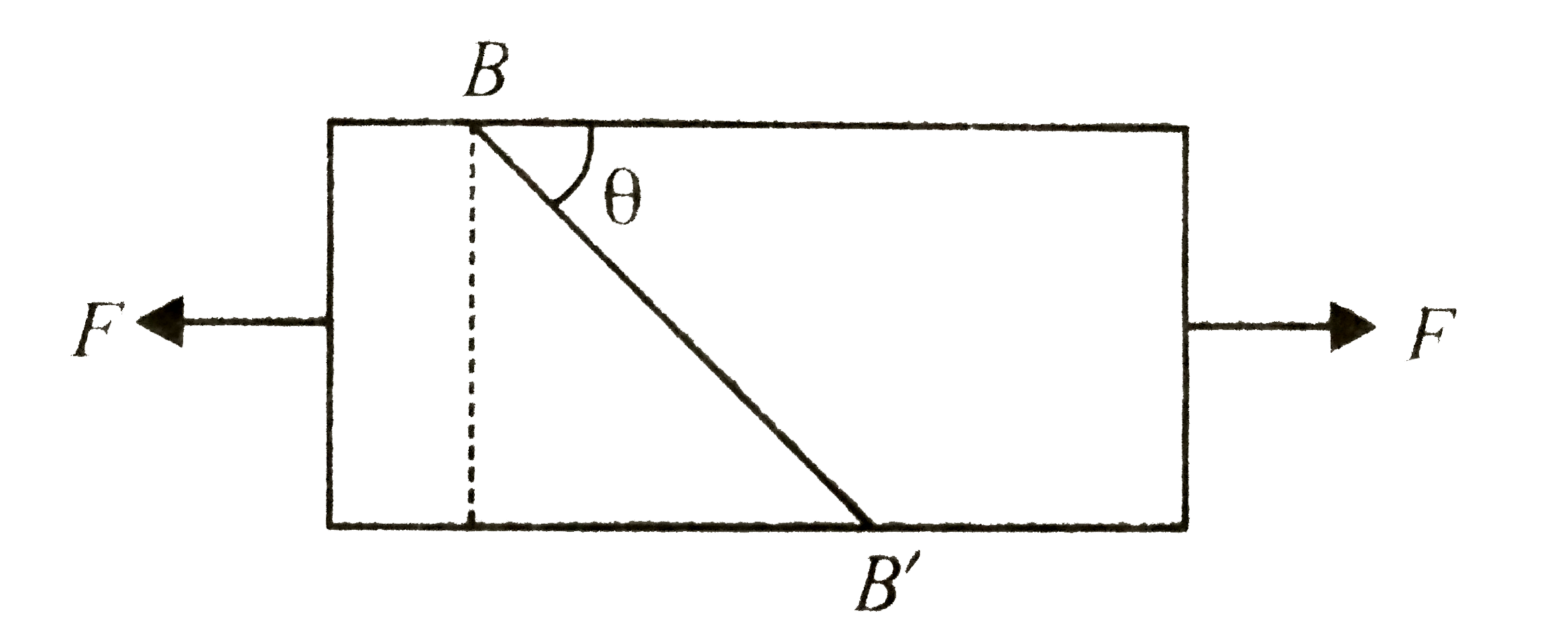
View SolutionA bar of cross- sectional area A is is subjected two equal and opposite tensile forces at its ends as shown in figure. Consider a plane BB' making an angle with length. The ratio of tensile stress to the shearing stress on the plane BB' is
View SolutionA bar of cross section is subjected to equal and opposite tensile force at its ends. Consider a plane section of the bar whose normal makes an angle with the axis of the bar.

a. What is the tensile stress on the plane?
b. What is the shearing stress on the this plane?
c. For what value of is the tensile stress maximum?
d. For what value of is the shearing stress maximum?
View SolutionA bar of cross-section A is subjected two equal and opposite tensile forces at its ends consider a plane section of the bar whose makes an angle with the axis of the bar.
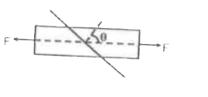
(a) what is the tensile stress on this plane ?
(b)what is the shearing stress on this plane ?
(c )for what value of is the tensile stress is maximum ?
(d) for what value of is the shearing stress maximum ?
View SolutionA bar of cross section is subjected to equal and opposite tensile force at its ends. Consider a plane section of the bar whose normal makes an angle with the axis of the bar.

a. What is the tensile stress on the plane?
b. What is the shearing stress on the this plane?
c. For what value of is the tensile stress maximum?
d. For what value of is the shearing stress maximum?
View SolutionA bar of cross-section A is subjected two equal and opposite tensile forces at its ends consider a plane section of the bar whose makes an angle with the axis of the bar.

(a) what is the tensile stress on this plane ?
(b)what is the shearing stress on this plane ?
(c )for what value of is the tensile stress is maximum ?
(d) for what value of is the shearing stress maximum ?
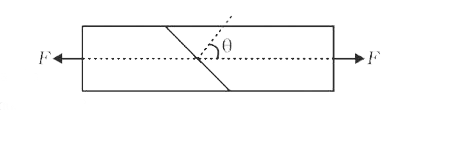
View SolutionA bar of cross-section A is subjected to equal and opposite tensile forces at its ends. Consider a plane section of the bar whose normal makes an angle theta with the axis of the bar . (i) What is the tensile stress on this plane? (ii) What is the shearing stress on this plane? (iii) For what value of theta is the tensile stress maximum (iv) For what value of theta is the shearing stress maximum?
View SolutionA bar of cross-section A is subjected to equal and opposite tensile forces at its ends. Consider a plane section of the bar whose normal makes an angle with the axis of the bar .
(i) What is the tensile stress on this plane?
(ii) What is the shearing stress on this plane?
(iii) For what value of is the tensile stress maximum
(iv) For what value of is the shearing stress maximum?
View Solutionअनुप्रस्थ परिच्छेद क्षेत्रफल A की किसी छड़ के सिरों पर चित्रानुसार दो समान एवं विपरीत तनन बल आरोपित किये जाते हैं । माना एक समतल BB' लम्बाई से कोण बनाता है।
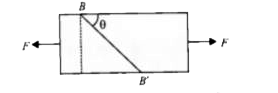
समतल BB' पर तनन प्रतिबल से अपरूपक प्रतिबल का अनुपात क्या होगा?
View SolutionA bar of cross section A is subjected to equal and opposite tensile forces F at its ends. Consider a plane through the bar making an angle with a plane at right angles to the bar as shown in figure.
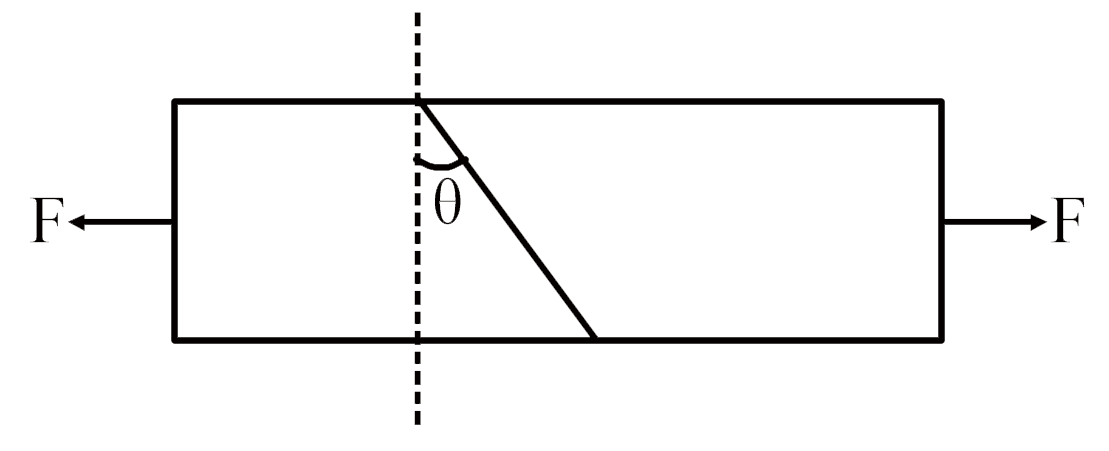
In the above problem, for what value of is the tensile stress maximum ?
View SolutionA अनुप्रस्थ काट क्षेत्रफल वाली एक छड़ के सिरों पर समान तथा विपरीत तनन बल F लगाया जाता है। छड़ से होकर गुजर रहे एक तल पर विचार कीजिये जो छड़ की लम्बाई के लम्बवत् तल के साथ कोण बनाता है।
(a) F, A तथा के पदों में इस तल पर तनन प्रतिबल क्या है ?
(b) F, A तथा के पदों में इस तल पर अपरूपण प्रतिबल क्या है ?

View Solution