A magnetic field in a certain region is given by B = Bo cosωt k and a coil of radius a with resistance R is placed in the x-y plane with its centre at the origin in the magnetic field see Fig 6.6 . Find the magnitude and the direction of the current at a 0 0 at t = π/2ω t = π/ω and t = 3π/2ω.
Flux through the ring
Related Solutions
A magnetic field in a certain region is given by and a coil of radius a with resistance R is placed in the xy-plane with its centre at the origin in the magnetic field (see figure). Find the magnitude and the direction of the current at (a, 0, 0) at and .
View SolutionA magnetic field in a certain region is given by and a coil of radius a with resistance R is placed in the x-y plane with its centre at the origin in the magnetic field, Fig. Find the magnitude and the direction of the current at (a,0,0) and .
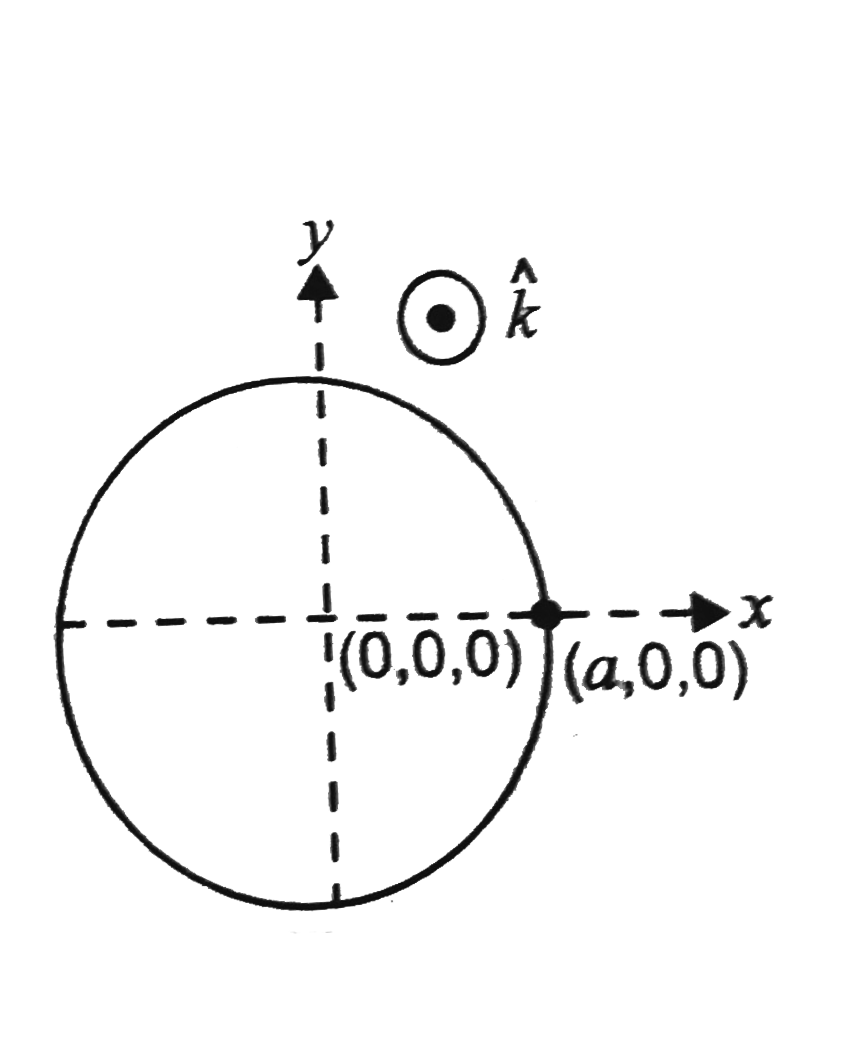
View SolutionA magnetic field in a certain region is given by B = B_(0) cos (omega t) hat k and a coil of radius a with resistance R is placed in the x-y plane with its centre at the origin in the magnetic field, Fig. Find the magnitude and the direction of the current at (a,0,0) at t = pi//2 omega, t = pi//omega and t = 3 pi//2 omega .
View SolutionAt a given point B=B_(0)cos (omega t)hatk Is expressed by and in this magnetic field x-y At the bottom is placed a coil of resistance R and radius a with its center at the origin. At the point (a, 0,0) t=(pi)/(omega),t=(pi)/(omega) And t=(3pi)/(2omega) Find the magnitude and direction of current at times.
View SolutionA magnetic field in a certain region is given by bar and a coil of radius a with resistanc R is placed i the XY-plane with its centre at the origin in the magnetic field as shown in the figure. Find the magnitude and direction of current at (a,0,0) at
View SolutionA uniform magnetic field is restricted within a region of radius r. The magnetic field changes with time at a rate . Loop 1 of radius R r encloses the region r and loop 2 of radius R is outside the region of magnetic field as shown in figure. Then, the emf generated is
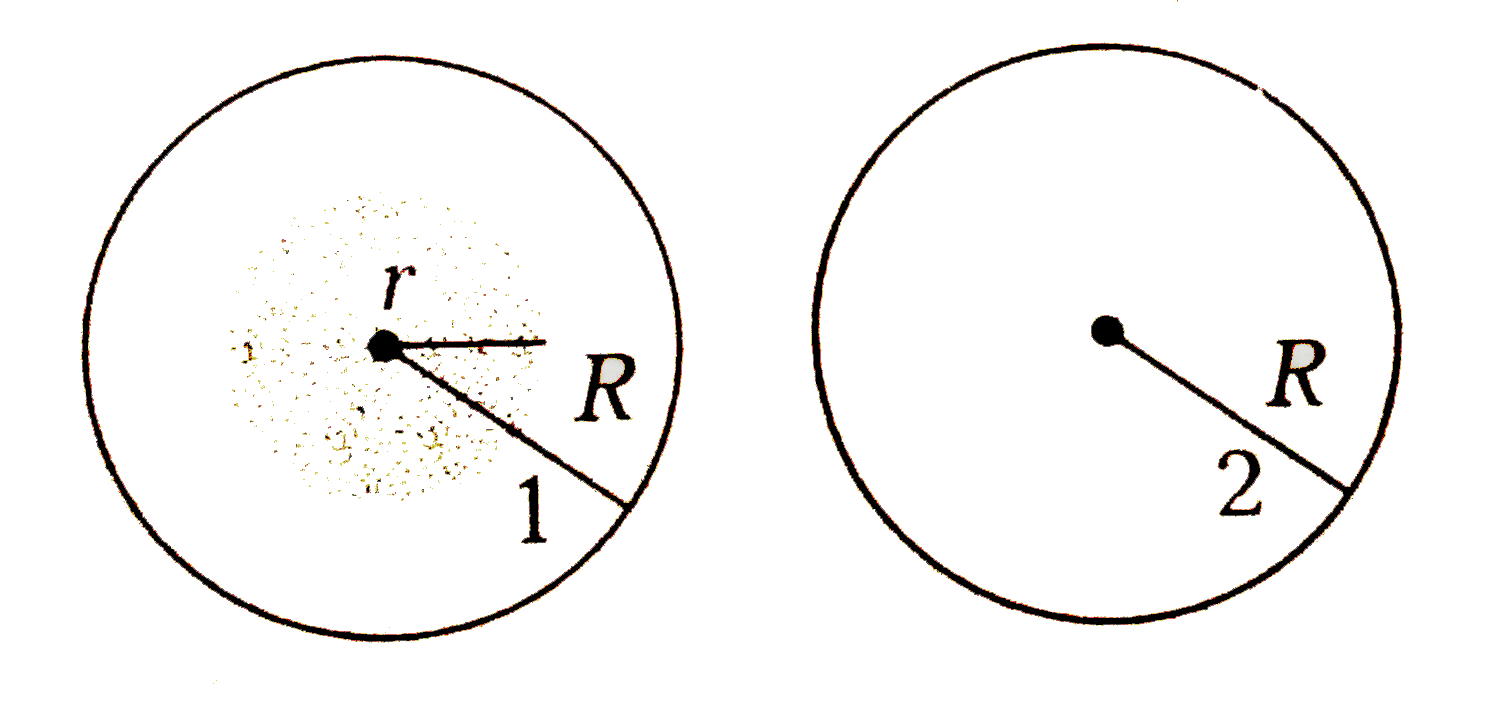
Zero in loop 1 and zero in loop 2
− d B d t π r 2 in loop 1 and − d B d t π 2 in loop 2
− d B d t π R 2 in loop 1 and zero in loop 2
− d B d t π r 2 in loop 1 and zero in loop 2
View SolutionShows a coil placed in a decreasing magnetic field applied perpendicular to the plane of the coil. The magnetic field is decreasing at a rate of . Find out current in magnitude and direction of current.

View SolutionShows a coil placed in a decreasing magnetic field applied perpendicular to the plane of the coil. The magnetic field is decreasing at a rate of 10 T s^(-1) . Find out current in magnitude and direction of current.
View SolutionShows a coil placed in a decreasing magnetic field applied perpendicular to the plane of the coil. The magnetic field is decreasing at a rate of . Find out current in magnitude and direction of current.

View SolutionA rectangular coil has turns and carries a current of . It is placed in a uniform magnetic field with the direction of magnetic field parallel to the plane of the coil. The magnitude of the torque required to hold this coil in this position is
View SolutionA rectangular coil 20cmxx20cm has 100 turns and carries a current of 1 A . It is placed in a uniform magnetic field B=0.5 T with the direction of magnetic field parallel to the plane of the coil. The magnitude of the torque required to hold this coil in this position is
View SolutionA rectangular coil 20cmxx20cm has 100 turns and carries a current of 1 A . It is placed in a uniform magnetic field B=0.5 T with the direction of magnetic field parallel to the plane of the coil. The magnitude of the torque required to hold this coil in this position is
View SolutionA rectangular coil has turns and carries a current of . It is placed in a uniform magnetic field with the direction of magnetic field parallel to the plane of the coil. The magnitude of the torque required to hold this coil in this position is
View SolutionIn a cylindrical region of radius a, magnetic field exists along its axis but the direction of magnetic field is opposite in the four quadrants of the region as shown in Fig. A or AB rotates with its end A at the centre of magnetic field and other end B slides on a smooth wire at the periphery of the region of magnetic field. At the rod was situated along the +X direction.
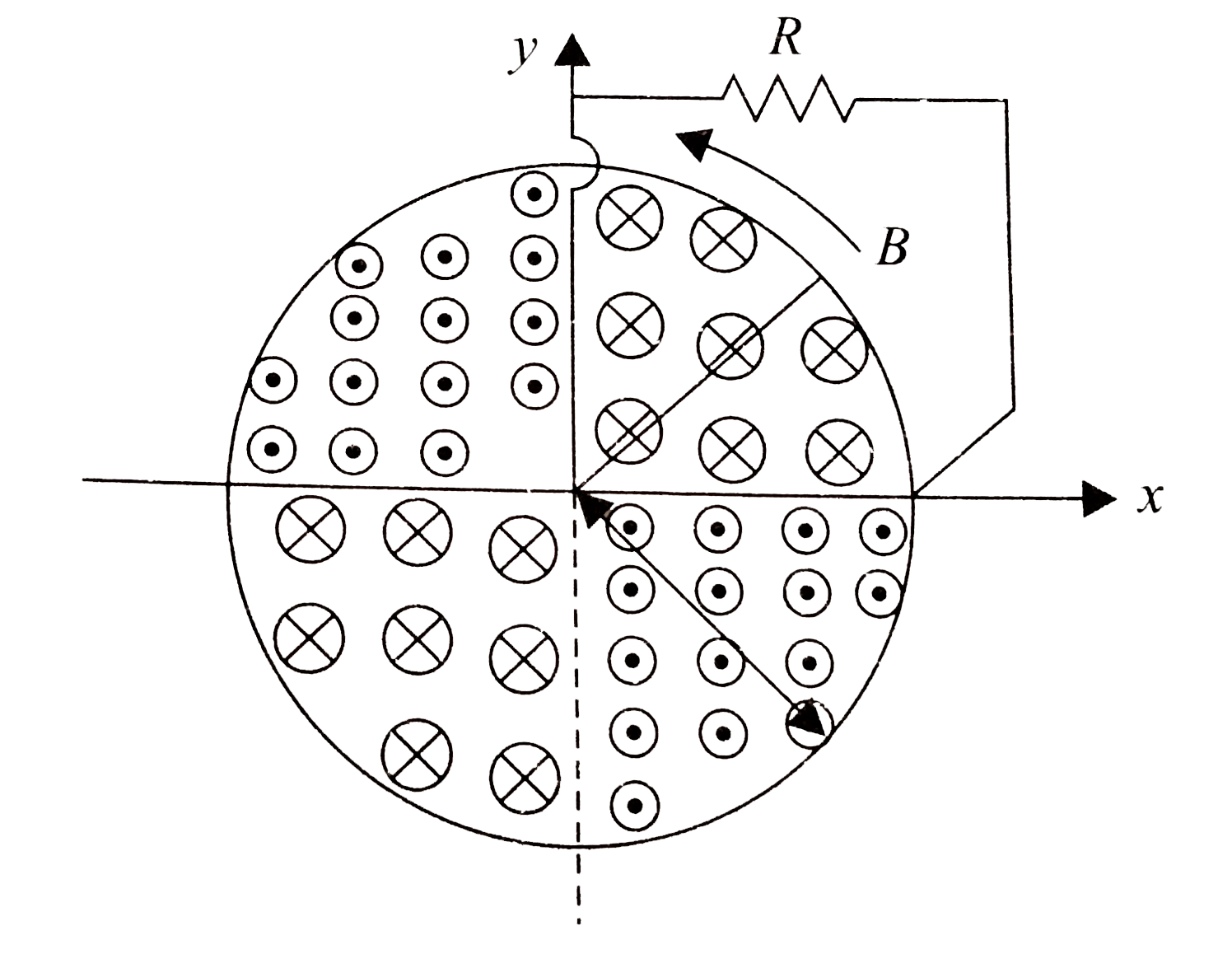
Find and plot the time dependence of the current in the resistance R when rod rotates with a constant angular velocity .
View SolutionIn a cylindrical region of radius a, magnetic field exists along its axis but the direction of magnetic field is opposite in the four quadrants of the region as shown in Fig. A or AB rotates with its end A at the centre of magnetic field and other end B slides on a smooth wire at the periphery of the region of magnetic field. At the rod was situated along the +X direction.

Find and plot the time dependence of the current in the resistance R when rod rotates with a constant angular velocity .
View SolutionIn a cylindrical region of radius a, magnetic field exists along its axis but the direction of magnetic field is opposite in the four quadrants of the region as shown in Fig. A or AB rotates with its end A at the centre of magnetic field and other end B slides on a smooth wire at the periphery of the region of magnetic field. At t = 0 the rod was situated along the +X direction. Find and plot the time dependence of the current in the resistance R when rotates with a constant angular acceleration (alpha)
View SolutionIn a cylindrical region of radius a, magnetic field exists along its axis but the direction of magnetic field is opposite in the four quadrants of the region as shown in Fig. A or AB rotates with its end A at the centre of magnetic field and other end B slides on a smooth wire at the periphery of the region of magnetic field. At t = 0 the rod was situated along the +X direction.
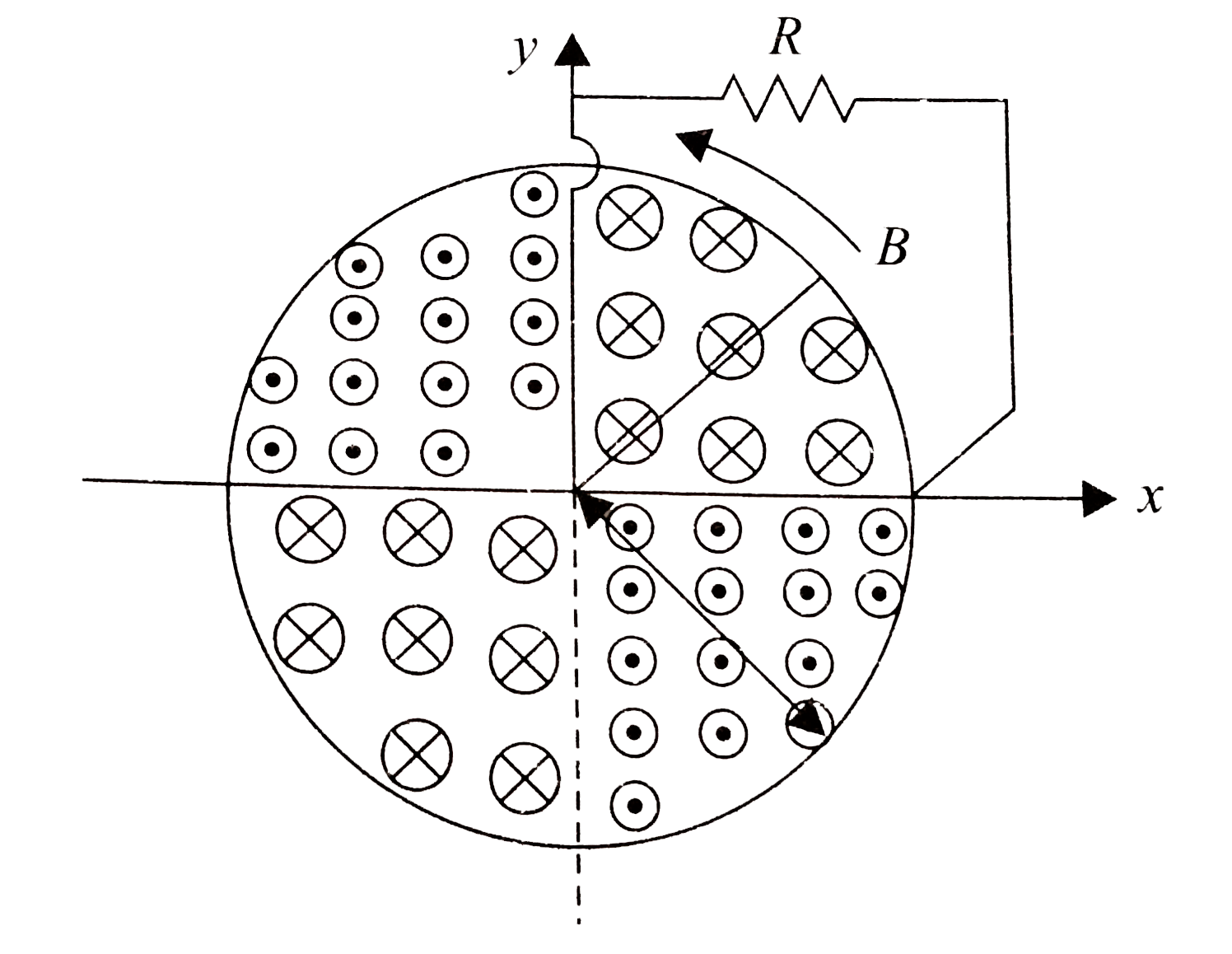
Find and plot the time dependence of the current in the resistance R when rotates with a constant angular acceleration
View SolutionA metallic ring is dropped down, keeping its plane perpendicular to a constant and horizontal magnetic field. The ring enters the region of magnetic field at t=0 and completely emerges out at t=T sec. The current in the ring varies as:
View SolutionA circular conducting coil of radius a and resistance R is placed with its plane perpendicular to a magnetic field. The magnetic field varies with time according to the equation B=B_(0)sinomegat . Obtain the expression for the induced current in the coil.
View SolutionA coil placed in a magnetic field decreasing at a rate of . There is also a source of emf in the coil. Find the magnitude and direction of the current in the coil.

View Solution