A plank with a body of mass m placed on it starts moving straight up according to the law y = a1 —cosωt where y is the displacement from the initial position ω = 11s-1. Find:a the time dependence of the force that the body exerts on the plank if a = 4.0cm; plot this dependence;b the minimum amplitude of oscillation of the plank at which the body starts falling behind the plank;c the amplitude of oscillation of the plank at which the body springs up to a height h = 50cm relative to the initial position at the moment t = 0.
a For the block from Newtons second law in projection form Fy = mwyN - mg = my 1But from y = a1 - cosωtwe get y = ω2acosωt 2From eqn 1 and 2From Newtons third law the force by which the body m exert on the block is directed vertically downward and equlsb When the body m starts falling behind the plank or losing contact N = 0 because the normal reaction is the contact force. Thus from eqn. 3c We observe that the motion takes place about the mean position y = a. At the initial instant y = 0. As shown in b the normal reaction vanishes at a height g/ω2 above the position of equilibrium and the body flies off as a free body. the speed of the body at a distance g/ω2 from the equilibrium position is ω√a2 - g/ω22 so that the condition of the problem givesHence solving the resulting quadratic equation and taking the positive roof
Related Solutions
A plank with a body of mass places on it starts moving straight up according to the law , whee is the displacement from the initial position, . Find :
(a) the time dependence of the force that the body exerts on the plank if plot this dependence,
the minimum amplitude of oscillation of the plank atwhich the body starts falling behind the plank,
(c) the amplitude of oscillation of the plank at which the body springs up to a height relative to the initial position (at the moment .
View SolutionA plank with a body of mass m placed on it starts moving straight up according to the law y=a(1-cosomegat), where y is the displacement from the initial position, omega=11s^(-1) . Find the minimum amplitude of oscillation of the plank at which the body starts falling behind the plank.
View SolutionA plank with a body of mass m placed on it starts moving straight up according to the law where y is the displacement from the initial position, . Find:
The time dependence of the force that the body exerts on the plank if a=4.0cm.
View SolutionA plank with a body of mass placed on it starts moving straight up according to the law , where is the displacement from the initial position, . Find
(a) The time independence of the force that the body exerts on the plank.
(b) The minimum amplitude of oscillations of the plank at which the body starts falling behind the plank.
View SolutionA plank with a body of mass placed on it starts moving straight up according to the law , where is the displacement from the initial position, . Find
(a) The time independence of the force that the body exerts on the plank.
(b) The minimum amplitude of oscillations of the plank at which the body starts falling behind the plank.
View SolutionA plank with a body of mass m placed on it starts moving straight up according to the law y=a(1-cosomegat), where y is the displacement from the initial position, omega=11s^(-1) . Find the amplitude of oscillation of the plank at which the body spring up to a height h=50 cm relative to the initial position (at the moment t=0)
View SolutionA bar of mass m_(1) is placed on a plank of mass m_(2) which rests on a smooth horizontal plane . The coefficient of friction between the surfaces of bar and plank is k . The plank is subjected to a horizontal force F depending on time t as F = at , where a is a constant . The moment of time t_(0) at which the plank starts sliding is :
View SolutionVertical displacement of a plank with a body of mass m on it is varying according to the law . The minimum value of for which the mass just breaks off the plank and the moment it occurs first time after t=0, are given by (y is positive towards vertically upwards).
View SolutionVertical displacement of a plank with a body of mass m on it is varying according to the law . The minimum value of for which the mass just breaks off the plank and the moment it occurs first time after t=0, are given by (y is positive towards vertically upwards).
View SolutionVertical displacement of a plank with a body of mass m on it is varying according to the law y=sinomegat+sqrt(3)cosomegat . The minimum value of omega for which the mass just breaks off the plank and the moment it occurs first time after t=0, are given by (y is positive towards vertically upwards).
View SolutionA plank of mass 'm' and area of cross - section A is floating as shown in figure. When slightly displaced from mean position, plank starts oscillations. Find time period of these oscillations.
View SolutionA plank of mass 'm' and area of cross - section A is floating as shown in figure. When slightly displaced from mean position, plank starts oscillations. Find time period of these osillations.
View SolutionA horizontal plank has a rectangular block placed on it. The plank starts oscillating vertically and simple harmonically with an amplitude of 40 cm. the block just loose contact with the plank when the plank is at momentary rest. Then
View SolutionVertical displacement of a plank with a body of mass 'm' on it is varying according to law y=sin omegat +sqrt(3) cos omegat . The minium value of omega for which the mass just breaks off the plank and the moment it occurs first arter t=0 are given by: (y "is positive vertically upwards")
View SolutionAs shown in the figure, a small block A whose mass is m is placed on the left side by a plan B whose mass is M = 2m and length is l. These bodies can slip on the moral road. The body starts moving with v initial velocity on the right. Find the coefficient of friction between the road and the plank, 1 // 2 and the coefficient of friction between the plank and the block is 1 // 4. Find the relative displacement of the plank to the earth up to the above moment.
View SolutionA man of mass m is moving with a constant acceleration a w.r.t. plank. The plank lies on a smooth horizontal floor. If mass of plank is also m then the frictional force exerted by plank on man is ma/k. Find the value of k.
View SolutionA man of mass m is moving with a constant acceleration a w.r.t. plank. The plank lies on a smooth horizontal floor. If mass of plank is also m then the frictional force exerted by plank on man is ma/k. Find the value of k.
View SolutionTwo men and are standing on a plank. is at the middle of the plank and is at the left end of the plank. Lower surface of the plank is smooth. System is initially at rest and masses are as shown in Fig. and start moving such that the position of remains fixed with respect to ground, then meets . Then the point where meets is located at
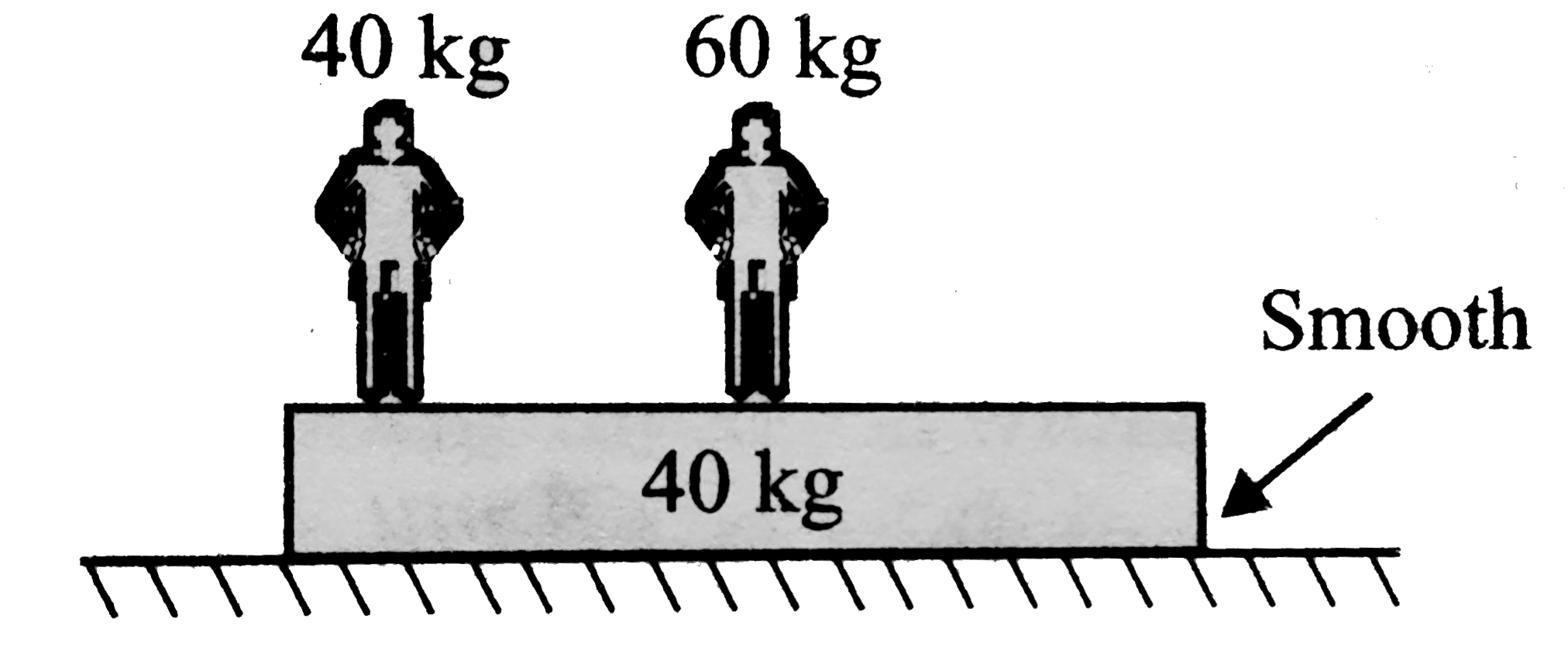
View SolutionTwo men 'A' and 'B' are standing on a plank. 'B' is at the middle of the plank and 'A' is at the left end of the plank. Lower surface of the plank is smooth. System is initially at rest and masses are as shown in Fig. 'A' and 'B' start moving such that the position of 'B' remains fixed with respect to ground, then 'A' meets 'B' . Then the point where A meets B is located at
View SolutionTwo men 'A' and 'B' are standing on a plank. 'B' is at the middle of the plank and 'A' is at the left end of the plank. Lower surface of the plank is smooth. System is initially at rest and masses are as shown in Fig. 'A' and 'B' start moving such that the position of 'B' remains fixed with respect to ground, then 'A' meets 'B' . Then the point where A meets B is located at
View Solution