Prove that the sum of the three sides of a triangle is greater than the sum of its three median.
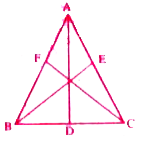
Given : A ΔABC with AD Be and CF as medians.To prove : AB + BC + CA > AD + BE + CFProof : Since AD is median with D as point of BCAB + AC > 2AD ....iBE is median with E on AC AB + BC > 2BE ....iiCF is median on side ABAC + BC > 2CF ....iiiAdding i ii and iii 2AB + BC + CA > 2AD + BE + CFor AB + BC + CA > AD + BE + CF=>Sum of the three sides of triangle is greater than its three median.
Related Solutions
सिद्ध करें कि त्रिभुज की तीनों भुजाओं का योग इसकी माध्यिकाओं के योग से अधिक है
View SolutionProve that the sum of the three sides of a triangle is greater than the sum of its three medians.
View Solutionसिद्ध कीजिए कि किसी त्रिभुज की तीनों माध्यिकाओं का योग, तीनों भुजाओं के योग से कम होता है।
View SolutionProve that the perimeter of a triangle is greater than the sum of its three medians.
View SolutionProve that the perimeter of a triangle is greater than the sum of its three medians.
View Solutionसिद्ध कीजिए कि किसी त्रिभुज का परिमाप, तीनों माध्यिकाओं के योग से अधिक होता है।
View SolutionProve that the sum of three altitudes drawn from the vertices to opposite sides of a triangle is less than the sum of three sides.
or
Prove that the perimeter of a triangle is greater than the sum of three altitudes drawn from the vertices to opposite of a triangle.
View Solutionसिद्ध कीजिए कि एक त्रिभुज की तीन शीर्षलम्बों का योग , तीनों भुजाओं के योग से कम होता है ।
View Solutionसिद्ध करें कि किसी त्रिभुज का परिमाप उसके तीनों शीर्ष लम्बों के योग से अधिक होता है |
View SolutionSum of the three sides of a triangle is less than the sum of its three altitudes.
View Solutionसिध्द करो कि किसी भी त्रिभुज के तीनो शीर्ष लम्बो का योगफल उसकी तीनों भुजाओं के योगफल से कम होता है |
View SolutionFor any triangle, prove that the sum of the sides of the triangle is greater than the sum of the medians of the triangle.
View Solutionसिद्ध कीजिए कि एक त्रिभुज में तीनों शीर्षो से सम्मुख भुजाओं पर डाले गये लम्बो का योग, तीनों भुजाओं के योग से छोटे होता है।
View SolutionProve that sum of any two medians of a triangle is greater than the third median.
View SolutionProve that the two medians of the triangle . The sum is greater than the third median.
View SolutionProve that the perimeter of any triangle is greater than the sum of three altitudes.
View SolutionProve that three xx the sum of the squares of the sides of a triangle is equal to fourxx the sum of the squares of the medians of the triangle.
View SolutionProve that three times the sum of the squares on the sides of a triangle is equal to four times the sum of the square on the medians of the triangle.
View SolutionProve that three times the sum of the squares of the sides of a triangle is equal to four times the sum of the squares of the medians of the triangle.
View SolutionProve that three times the sum of the squares of the sides of a triangle is equal to four times the sum of the squares of the medians of the triangle.
View Solution