Prove that the perimeter of any triangle is greater than the sum of three altitudes.
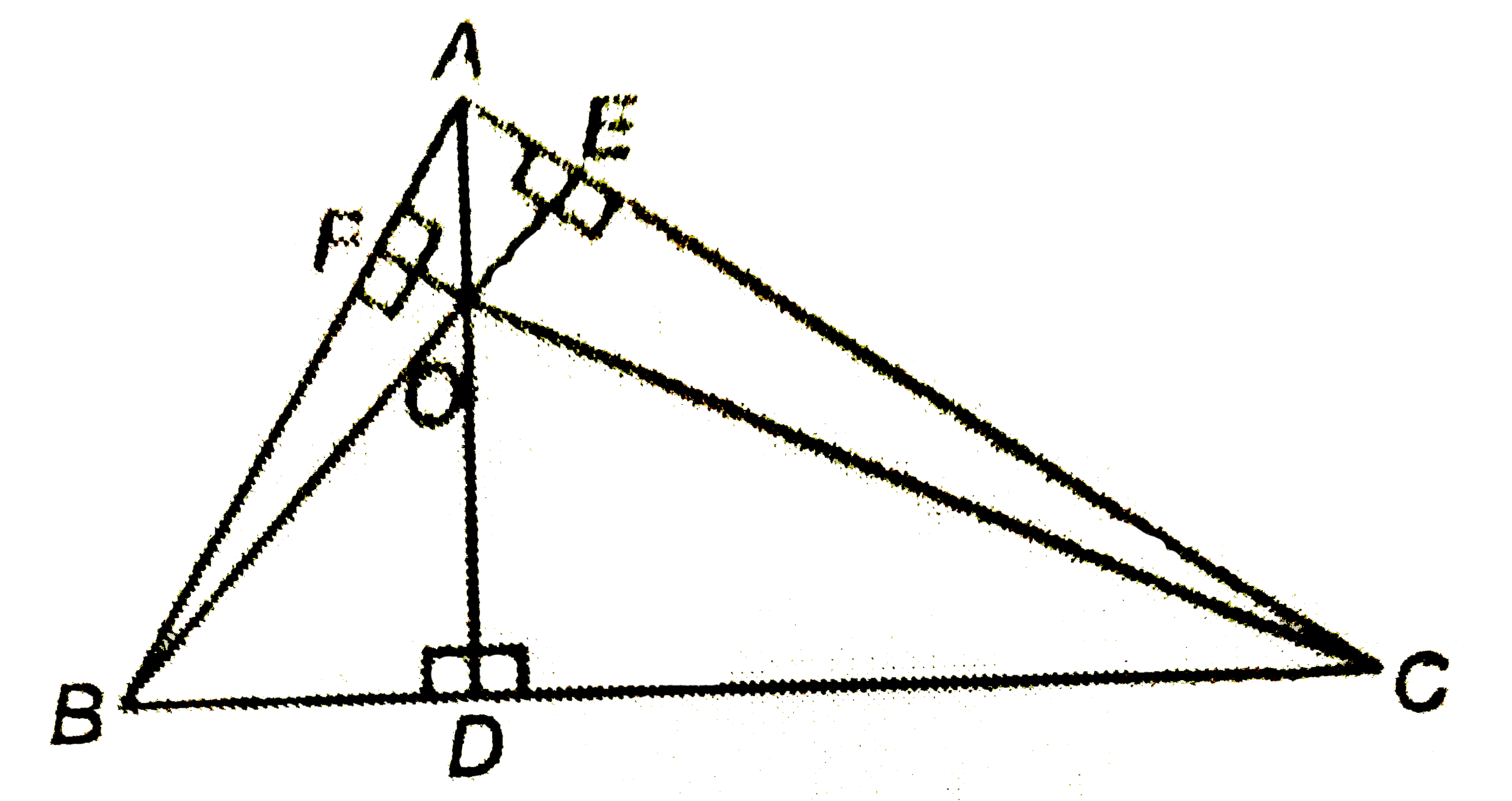
Given : ABC is a triangle in which AD, BE and CF are perpendiculars.
To Prove : AB+BC+CA>AD+BE+CF
Proof : Since in a right angled triangle, hypotenuse is the longest side.
∴ In right ΔABD, AB>AD ...(1)
(side opposite to greater angle is longer)
In right ΔBEC, BC>BE ...(2)
(side opposite to greater angle is longer)
In right ΔAFC, AC>CF (side opposite to greater angle is longer) ...(3)
Adding (1), (2) and (3), we get
AB+BC+CA>AD+BE+CF Hence Proved.
Topper's Solved these Questions
- TRIANGLESBook:NAGEEN PRAKASHANChapter:TRIANGLESExercise:Problems From NCERT/exemplar
Explore 5 Videos
- TRIANGLESBook:NAGEEN PRAKASHANChapter:TRIANGLESExercise:Exercise 7a
Explore 35 Videos
- SURFACE AREA AND VOLUMEBook:NAGEEN PRAKASHANChapter:SURFACE AREA AND VOLUMEExercise:Revision Exercise (long Answer Questions)
Explore 10 Videos
Similar Questions
Prove that the sum of three altitudes drawn from the vertices to opposite sides of a triangle is less than the sum of three sides.
or
Prove that the perimeter of a triangle is greater than the sum of three altitudes drawn from the vertices to opposite of a triangle.
View SolutionProve that the perimeter of a triangle is greater than the sum of its altitudes.
View Solution
Knowledge Check
Consider the following statements in respect of any triangle
I. The three medians of a triangle divide it into six triangles of equal area.
II. The perimeter of a triangle is greater than the sum of the lengths of its three medians.
Which of the statements given above is/are correct ?AI onlyBII onlyCBoth I and IIDNeither I nor II
Prove that the perimeter of a triangle is greater than the sum of its three medians.
View SolutionProve that the perimeter of a triangle is greater than the sum of the three medians.
View SolutionProve that the perimeter of a triangle is greater than the sum of its three medians. In the△ABC, D,E and F are the midpoints of sides BC,CA and AB respectively.
View SolutionConsider the following statements :
1. The perimeter of a triangle is greater than the sum of its three medians.
2. In any triangle ABC, if D is any point on BC, then AB + BC + CA > 2AD.
Which of the above statements is/are correct?
View SolutionWhich of the following statements are true (T) and which are false (F)? Sum of the three sides of a triangle is less than the sum of its three altitudes. Sum of any two sides of a triangle is greater than twice the median drawn to the third side. Sum of any two sides of a triangle is greater than the third side. Difference of any two sides of a triangle is equal to the third side. If two angles of a triangle are unequal, then the greater angle has the larger side opposite to it. Of all the line segments that can be drawn from a point to a line not containing it, the perpendicular line segment is the shortest one.
View SolutionSum of any two sides of a triangle is greater than the third side.
View SolutionShow that the sum of the three altitudes of a triangle is less than the sum of three sides of the triangle.
View Solution

