A tower stands at the centre of a circular park. A and B are two points on the boundary of the park such that AB = a subtends an angle of 60° at the foot of the tower and the angle of elevation of the top of the tower from A or B is 30°. The height of the tower isa a/√3 b a√3c 2a/√3 d 2a√3.
The correct answer is:
Related Solutions
A tower stands at the centre of a circular park. A and B are two points on the boundary of the park such that AB(=a) subtends an angle of 60^(@) at the foot of the tower,and the angle of elevation of the top of the tower from A or B is 30^(@). The height of the tower is (1) (2a)/(sqrt(3)) (2) 2a sqrt(3)(3)(a)/(sqrt(3))(4)a sqrt(3)
View SolutionA tower stands at the centre of a circular park . A and B are two points on the boundary of the park such that AB(=a) subtends an angle of 60^@ at the foot of the tower , and the angle of elevation of the top of the tower from A or B is 30^@ . The height of the tower is
View SolutionA tower stands at the centre of a circular park . A and B are two points on the boundary of the park such that AB(=a) subtends an angle of 60^@ at the foot of the tower , and the angle of elevation of the top of the tower from A or B is 30^@ . The height of the tower is
View SolutionA Tower stands at the centre of a circular park. A and B are two points on the boundary of the park such that AB (a) subtends an angle of 60^(@) at the foot of the tower, and the angle of elevation of the top of the tower from A or B is 30°. The height of the tower is
View SolutionA tower stands at the centre of a circular park. A and B are two points on the boundary of the park such that AB(=a) subtends an angle 60^(@) at the foot of the tower, and the angle of elevation of the top of the tower from A or B is 30^(@) . The height of the tower is:
View SolutionA tower stands at the centre of a circular park. A and B are two points on the boundary of the park such that AB . (= a) subtends an angle of 60^@ at the foot of the tower, and the angle of elevation of the top of the tower from A or B is 30^@ . The height of the tower is
View SolutionA tower stands at the centre of a circular park .A and B are two points on the boundary of the park such that AB = (=a) subtends an angle of 60^@ at the foot of the tower ,and the angle of elevation of the top of the tower from A or B is 30^@ the height of hte tower is
View SolutionA tower stands at the center of a circular park. A and B are two points on the boundary of the park such that AB(=a) subtends an angle of 60^(@) at the foot of the tower, and the angle of elevation of the top of the tower from A or B is 30^(@) . The height of the tower is
View SolutionA tower stands at the centre of a circular park. A and B are two points on the boundary of the park such that A B""(=""a) subtends an angle of 60^@ at the foot of the tower, and the angle of elevation of the top of the tower from A or B is 30^@ . The height of the tower is (1) (2a)/(sqrt(3)) (2) 2asqrt(3) (3) a/(sqrt(3)) (4) asqrt(3)
View SolutionA tower stands at the centre of a circular park. A and B are two points on the boundary of the park such that AB (= a) subtends an angle of 60^(@) at the face of the lower and the angle of elevation of the top of the tower from A or Bis 30^(@). The height of the tower is:
View SolutionA tower stands at the centre of a circular park. A and B are two points on the boundary of the park such that AB(=alpha) subtends an angle of elevation of the top of the first tower from A or B is 30^@ . The height of the tower is
View SolutionA tower is at the center of a circular Bigache. A and B are two points on the edge of the garden such that AB (= a) is at the foot of the tower. 60^(@) The angle of elevation and the elevation angle of the top of the tower from A or B 30^(@) is. The height of the tower is.
View SolutionThe angle of elevation of the top of a tower from a point A on the ground is . On moving a distance of 20 metres towards the foot of the tower to a point B, the angle of elevation increases to . Find the height of the tower and distance of the tower from the point A.
View SolutionABC is a triangular park with A Television tower stands at the mid point of BC. The angles of elevations of the top of tower at A,B,C are respectively Then the height of tower is
View SolutionA vertical tower subtends an angle of at a point on the same level as the foot of the tower. On moving 100 m further in line with the tower, it subtends an angle of at the point. Then, the height of the tower, it subtends an angle of at the point. Then, the height of the tower is
View SolutionA tower stands vertically on the ground. From a point on the ground, 20m away from the foot of the tower, the angle of elevation of the top of the tower is . What is the height of the tower?
View SolutionHeight of a tower is metres. The angle to elevation of the top the tower from a point at a distance of 100 metres of foot of the tower is
View SolutionThe angle of elevation of the top of a hill from the foot of a tower is and the angle of elevation of the top of the tower from the foot of the hill is . If the tower is 50 m high, then what is the height of the hill?
View SolutionIn figure, the angle of elevation of the top of a tower AC from a point B on the ground is . If the height of the tower is 20m , find the distance of the point from the foot of the tower.
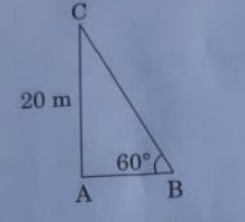
View SolutionIn figure, the angle of elevation of the top of a tower AC from a point B on the ground is . If the height of the tower is 20m , find the distance of the point from the foot of the tower.
View Solution